2、概率的几种定义
[频率与概率] 随机事件在一次试验中是否发生,固然是无法事先肯定的偶然现象,但当进行多次重复试验,就可以发现其发生的可能性大小的统计规律性。具体说,如果在相同条件下进行n次重复试验,事件A出现了v次,那末事件A在n次试验中出现的频率![]() 当n无限增大时呈现稳定性。这一统计规律性表明事件A发生的可能性大小是事件本身所固有的、不以人们主观意志改变的一种客观属性。事件A发生的可能性大小称为事件A的概率,记作P(A)。当试验的次数n足够大,可用事件的频率近似地表示该事件的概率,即
当n无限增大时呈现稳定性。这一统计规律性表明事件A发生的可能性大小是事件本身所固有的、不以人们主观意志改变的一种客观属性。事件A发生的可能性大小称为事件A的概率,记作P(A)。当试验的次数n足够大,可用事件的频率近似地表示该事件的概率,即
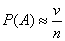
[概率的古典定义] 设一个随机试验(不能事先准确的预言它的结果,而且在相同条件下可以重复进行的试验)只有有限个不同的基本事件ω1 , ω2 , ··· ,ωn(基本事件也是一种事件,一般的事件总是有几个基本事件共同组成的),每个基本事件都是等可能*的,基本事件的全体记作Ω,称它为基本事件空间,如果事件A由k (k![]() n)
个不同的基本事件组成,那末规定A的概率P(A)为
n)
个不同的基本事件组成,那末规定A的概率P(A)为
![]()
不可能事件![]() 的概率规定为
的概率规定为
![]()
[概率的公理化定义]
定义 1 设![]() ,F
,F ![]() ,如果F满足下面条件:
,如果F满足下面条件:
(i)![]() F;
F;
(ii)
若![]() F,则
F,则![]() F(
F(![]() );
);
(iii) 对于任意![]() F
(n=1,2,···),有
F
(n=1,2,···),有
![]() F
F
则称F是![]() 中的一个
中的一个![]() 代数。
代数。
定义2 设![]() 是
是![]() 代数F上的实值集函数,如果它满足条件:
代数F上的实值集函数,如果它满足条件:
(i)
对任意![]() F,有0
F,有0![]() P(A)
P(A)![]() 1;
1;
(ii)
![]() ;
;
(iii)
对任意![]() F(n=1 , 2 , ···),Ai
F(n=1 , 2 , ···),Ai![]() Aj=
Aj=![]() ( i
( i![]() j
) 有
j
) 有
P(![]() )=
)=![]() An)
An)
则称P(A)为F上的概率测度,或简称概率。这时,称ω为基本事件,A(![]() F)称为事件,F是事件的全体,P(A)称为事件A的概率,<
F)称为事件,F是事件的全体,P(A)称为事件A的概率,<![]() ,F ,P>
,F ,P>![]() 称为概率空间。
称为概率空间。