4、概率的计算公式

[条件概率与乘法公式] 在事件B发生的条件下，事件A发生的概率称为事件A在事件B已发生的条件下的条件概率，记作P(A|B)。当P(B)>0时，规定

P(A|B)=

当P(B)=0时，规定P(A|B)=0。由此得出乘法公式：

P(A=P(B)P(A|B)=P(A)P(B|A)

         P(A₁A₂···A_n)=P(A₁)P(A₂|A₁)P(A₃|A₁A₂)···P(A_n|A₁A₂···A_n-1)        (P(A₁A₂···A_n-1)>0)

[独立性公式]  如果事件A与B满足P(A|B)=P(A)，那末称事件A关于事件B是独立的。独立性是相互的性质，即A关于B独立，B一定关于A独立，或称A与B相互独立。

   A与B相互独立的充分必要条件是：

                  P(AB)=P(A)P(B)

如果事件A₁ ,A₂ ,···, A_n中任意m个()都满足关系式

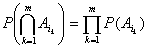
称A₁ , A₂ ,···, A_n是总起来独立的，简称为相互独立。

[全概率公式]  如果事件组B₁ , B₂ ,···满足

    

P()=1,   P(B_i)>0     (i=1,2,···)

则对于任意一事件A，有

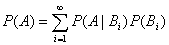
如果B_i只有n个，公式也成立，此时右端只有n项相加。

[贝叶斯公式]  如果事件组B₁ , B₂ ,···满足

  (ij)

,      

则对于任一事件A(P(A)>0)，有

P(B_i |A)=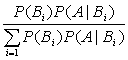

如果B_i只有n个，公式也成立，此时右端分母只有n项相加。

[伯努利公式]  设一次试验中某事件A出现的概率为p，则n次重复试验中事件A出现k次的概率p_n,k为

p_n,k = p^k(1)^n-k      (k=0,1,···,n)

式中为二项系数。

   当n和k都很大时，有近似公式

p_n,k

式中,  。

[泊松公式]  当n充分大，且p很小时，有近似公式

p_n,k

式中= np。