二、随机变量与分布函数
[随机变量及其概率分布函数] 每次试验的结果可以用一个变量![]() 的数值来表示,这个变量的取值随偶然因素而变化,但又遵从一定的概率分布规律,这种变量称为随机变量,用
的数值来表示,这个变量的取值随偶然因素而变化,但又遵从一定的概率分布规律,这种变量称为随机变量,用![]() ,···表示。它是随机现象的数量比。
,···表示。它是随机现象的数量比。
给定随机变量![]() ,它的取值不超过实数x的事件的概率P(
,它的取值不超过实数x的事件的概率P(![]()
![]() x)是x的函数,称为
x)是x的函数,称为![]() 的概率分布函数,简称分布函数,记作F(x) ,即
的概率分布函数,简称分布函数,记作F(x) ,即
F(x)=P(![]() (
(![]()
[分布函数的基本性质]
1° ![]() ,
,![]()
2° 若x1<x2,则F(x1)![]() F(x2) (单调性)
F(x2) (单调性)
3° F(x+0)=F(x) (右连续性)
4° P(a<![]() =F(b)
=F(b)![]() (a)
(a)
5° P(![]() =F(a)
=F(a)![]() 0)
0)
[离散分布与概率分布列] 如果随机变量![]() 只能取有限个或可列个数值x1 ,
x2 ,···, xn ,···,就称
只能取有限个或可列个数值x1 ,
x2 ,···, xn ,···,就称![]() 为离散型随机变量。若记P(
为离散型随机变量。若记P(![]() )=pk (k=1,2,···),则
)=pk (k=1,2,···),则![]() 取值的概率分布由{pk}完全确定。称{pk}为
取值的概率分布由{pk}完全确定。称{pk}为![]() 的概率分布列。{pk}有以下性质:
的概率分布列。{pk}有以下性质:
1° ![]()
2° ![]() =1
=1
3° 设D为实数轴上任一可测集,则P(![]()
4° ![]() 的分布函数
的分布函数
F(x)=![]()
是在![]() 处有跳跃
处有跳跃![]() 的阶梯函数。
的阶梯函数。
[连续分布与分布密度函数] 如果随机变量![]() 的分布函数F(x)能够表示为
的分布函数F(x)能够表示为
F(x)= ![]() (p (x)非负)
(p (x)非负)
就称![]() 是连续型随机变量。p(x)称为
是连续型随机变量。p(x)称为![]() 的分布密度函数(或分布密度)。分布密度函数具有以下性质:
的分布密度函数(或分布密度)。分布密度函数具有以下性质:
1° p(x)=![]()
2° ![]()
3° 若p (x)是连续型随机变量![]() 的分布密度,则对实数轴上的任一可测集D,有
的分布密度,则对实数轴上的任一可测集D,有
![]()
[随机变量的函数的分布] 如果随机变量![]() 是随机变量
是随机变量![]() 的函数
的函数
![]()
设随机变量![]() 的分布函数为F(x),则
的分布函数为F(x),则![]() 的分布函数G(x)为
的分布函数G(x)为
G(x)=![]()
特别,当![]() 是离散型随机变量时,其可能值为x1 , x2,···,且P
是离散型随机变量时,其可能值为x1 , x2,···,且P![]() ,则
,则
G(x)= ![]()
当![]() 是连续型随机变量时
,其分布密度为p(x),则
是连续型随机变量时
,其分布密度为p(x),则
G(x)= ![]()
[随机矢量的联合分布函数与边缘分布函数] 如果![]() ···,
···,![]() 联系于同一组条件下的n个随机变量,则称
联系于同一组条件下的n个随机变量,则称![]() ···,
···,![]() )为n维随机变量或随机矢量。
)为n维随机变量或随机矢量。
若(x1 , x2 ,···,xn)是n维实数空间Rn上的一点,则事件"![]()
![]() ···,
···,![]() "的概率
"的概率
![]()
作为x1 , x2 ,···, xn的函数,称为随机矢量![]() ···,
···,![]() 的联合分布函数。
的联合分布函数。
设(![]() ···,
···,![]() 是(
是(![]() ···,
···,![]() 中任意取出m(m
中任意取出m(m![]() n)个分量构成的m维随机变量,则称(
n)个分量构成的m维随机变量,则称(![]() ···,
···,![]() 的联合分布函数为(
的联合分布函数为(![]() ···,
···,![]() 的m维边缘分布函数。
的m维边缘分布函数。
这时,如果分别记(![]() ···,
···,![]() 与(
与(![]() ···,
···,![]() 的分布函数为F(x1,x2,···,xn)与
的分布函数为F(x1,x2,···,xn)与![]() ,那末
,那末
![]()
![]() =F(
=F(![]() ···,x
···,x![]() ,···,
,···,![]() ,···,x
,···,x![]() ,···,
,···,![]() )
)
[条件分布函数与独立性] 设![]() 是一随机变量,事件B满足P(B)>0,则称
是一随机变量,事件B满足P(B)>0,则称
F(x|B)=P (![]()
![]() x|B)
x|B)
为![]() 在事件B已发生的条件下的条件分布函数。
在事件B已发生的条件下的条件分布函数。
1° 设(![]() ,
,![]()
![]() 是二维离散型随机变量,
是二维离散型随机变量,![]() 和
和![]() 的可能取值分别为xi (i=1,2,···)和yk (k=1,2,···).又记(
的可能取值分别为xi (i=1,2,···)和yk (k=1,2,···).又记(![]() ,
,![]() 的联合分布为
的联合分布为
P(![]()
![]() =
pik
=
pik
两个一维边缘分布为
P(![]() =
=![]() ·=
·=![]() (i=1,2,···)
(i=1,2,···)
P(![]() =
=![]() =
=![]()
![]()
则称
P(![]() |
|![]() )=
)=![]()
![]()
为在![]() 条件下离散型随机变量
条件下离散型随机变量![]() 的条件分布。类似的,称
的条件分布。类似的,称
P(![]() |
|![]() )=
)=![]() (
(![]() >0,
k=1,2,···)
>0,
k=1,2,···)
为在![]() 条件下离散型随机变量
条件下离散型随机变量![]() 的条件分布。
的条件分布。
2° 设(![]() )是二维连续型随机变量,其联合分布密度是f(x,y),在点y ,
)是二维连续型随机变量,其联合分布密度是f(x,y),在点y ,![]() 则称
则称
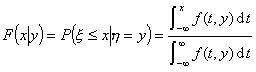
为![]() 在
在![]() =y条件下的条件分布函数,在点x,
=y条件下的条件分布函数,在点x,![]() 则称
则称
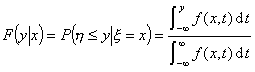
为![]() 在
在![]() 条件下的条件分布函数。
条件下的条件分布函数。
3° 如果(![]() ···,
···,![]() 的联合分布函数等于所有一维边缘分布函数的乘积,即
的联合分布函数等于所有一维边缘分布函数的乘积,即
F(x1 , x2
,···, xn)=![]()
(它相当于P(![]() ,···,
,···,![]()
![]() xn)=
xn)=![]() 那末称
那末称![]() ,···,
,···,![]() 是相互独立的。
是相互独立的。