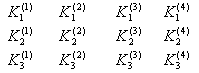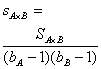五、正交试验设计
[正交表与正交试验] 正交表是根据组合理论,按照一定规律构造的表格,它在试验设计中有广泛的应用。以正交表为工具安排试验方案和进行结果分析的试验称为正交试验。它适用于多因素、多指标(试验需要考察的结果)、多因素间存在交互作用(因素之间联合起作用)、具有随机误差的试验。通过正交试验,可以分析各因素及其交互作用对试验指标的影响,按其重要程度找出主次关系,并确定对试验指标的最优工艺条件。在正交试验中要求每个所考虑的因素都是可控的。在整个试验中每个因素所取值的个数称为该因素的水平。
正交表的符号为![]() ,其中
,其中![]() 表示正交表;下标
表示正交表;下标![]() 是正交表的行数,表示试验次数;
是正交表的行数,表示试验次数;![]() 是正交表的列数,表示试验至多可以安排的因素个数;
是正交表的列数,表示试验至多可以安排的因素个数;![]() 是表中不同数字的个数,表示每个因素的水平数。例如
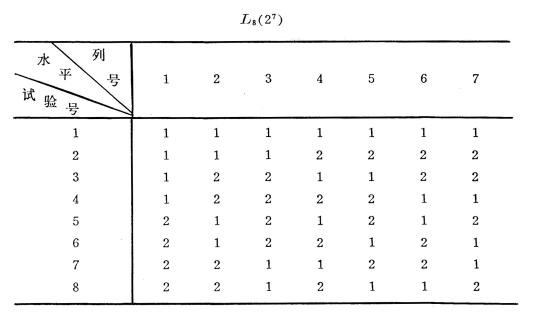
是表中不同数字的个数,表示每个因素的水平数。例如![]() ,8表示正交表中有8行,即安排试验的次数为8次;7表示正交表中有7列,试验至多可安排7个因素(包括交互作用的因素);2表示每个因素只有两个水平。这种正交表称为2水平型的正交表。
,8表示正交表中有8行,即安排试验的次数为8次;7表示正交表中有7列,试验至多可安排7个因素(包括交互作用的因素);2表示每个因素只有两个水平。这种正交表称为2水平型的正交表。
 |
又如
[正交表的交互列] 任意两列分别安排了两个因素之后,这两个因素的交互作用可用表的其他列表示出来,称为交互列。交互列在2水平型正交表中只有一列,在3水平型正交表中有两列,例如![]() ,任意两列的交互列是另外两列。通常低水平(水平数为2或3)的正交表有另外专表写出交互列,例如
,任意两列的交互列是另外两列。通常低水平(水平数为2或3)的正交表有另外专表写出交互列,例如![]() 的交互列表,指出第3列与第5列的交互列即是第6列等等。有些正交表,例如
的交互列表,指出第3列与第5列的交互列即是第6列等等。有些正交表,例如![]() ,任意两列的交互列都不在表内,对这样的正交表就不能考虑因素间的交互作用了。
,任意两列的交互列都不在表内,对这样的正交表就不能考虑因素间的交互作用了。
手册后面备有常用正交表。
![]() 的交互列表
的交互列表
|
1 2 3 4 5 6 7 |
列号 |
|
(1) 3 2 5 4 7 6 (2) 1 6 7 4 5 (3) 7 6 5 4 (4) 1 2 3 (5) 3 2 (6) 1 (7) |
1 2 3 4 5 6 7 |
[正交表的正交性] 正交表具有正交性:
1° 在任意一列中,每个水平的重复次数都相等,例如![]() 中每列的每个水平都重复4次。
中每列的每个水平都重复4次。
2° 任意两列中,同行数字(水平)构成的数对,包含着所有可能(该水平下)的数对,而每个数对重复次数相等。例如在![]() 中任意两列构成的数对都包含着3水平下所有可能的数对:(1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(3,1),(3,2),(3,3),而且每个数对重复次数都等于1。
中任意两列构成的数对都包含着3水平下所有可能的数对:(1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(3,1),(3,2),(3,3),而且每个数对重复次数都等于1。
由于正交性,使得所安排的正交试验,均衡分散,整齐可比。
[试验方案的制定步骤与安排方法]
1° 步骤
(1) 确定试验中变化因素的个数及每个因素变化的水平。
(2) 根据专业知识或经验,初步分析各因素之间的交互作用,确定哪些是必须考虑的,哪些是暂时可以忽略的。
(3) 根据试验的人力、设备、时间及费用,确定可能进行的大概试验次数。
(4) 选用合适的正交表,安排试验。
2° 安排方法
(1) 在不考虑交互作用时,把因素逐个安排在正交表的任意列上,那末每次试验(对应于正交表的行)的试验条件(每个因素应取的水平)由安排因素的各列的水平确定。
例如,在试验用不发芽的大麦造啤酒的过程中,选了四个因素,每个因素三个水平,指标是粉粒状(%)。
因素水平表
|
因素 水平 |
底水(A) 浸氨时间 (B) 920浓度 (C) 氨水浓度(D) |
|
1 2 3 |
A1(140) B1(180) C1(2.5) D1(0.25) A2(136) B2(215) C2(3.0) D2(0.26) A3(138) B3(250) C3(3.5) D3(0.27) |
如果不考虑交互作用,可选用正交表![]() ,得试验方案如下:
,得试验方案如下:
用![]() 安排一个四因素的试验方案
安排一个四因素的试验方案
|
列号(因素) 试验号 |
1(A) 2(B) 3(C) 4(D) |
|
1 2 3 4 5 6 7 8 9 |
1(A1) 1(B1) 1(C1) 1(D1) 1(A1) 2(B2) 2(C2) 2(D2) 1(A1) 3(B3) 3(C3) 3(D3) 2(A2) 1(B1) 2(C2) 3(D3) 2(A2) 2(B2) 3(C3) 1(D1) 2(A2) 3(B3) 1(C1) 2(D2) 3(A3) 1(B1) 3(C3) 2(D2) 3(A3) 2(B2) 1(C1) 3(D3) 3(A3) 3(B3) 2(C2) 1(D1) |
此表指出第1号试验的条件是![]() ,第2号试验条件是
,第2号试验条件是![]() 第9号试验的条件是
第9号试验的条件是![]() 。
。
(2) 需要考虑交互作用时,因素不能任意安排,应利用相应的表头设计安排试验。此时要注意不能使不同的因素(包括所考虑的交互作用)同处一列(因为分析时无法将同处一列的不同作用分析出来),如果做不到这一点,就需要采用更大的正交表。例如安排一个四因素A , B , C , D的试验,必须考虑交互作用![]() ,其他交互作用可忽略不计。根据
,其他交互作用可忽略不计。根据![]() 的表头设计:
的表头设计:
|
列号 因素个数 |
1 2 3 4 5 6 7 |
|
3 |
A B |
|
4 |
A B |
|
4 |
A |
|
5 |
|
因为是四因素试验,所以可将A ,
B , C , D分别安排在第1,2,4,7列上,第3,5列分别表示![]() 及
及![]() ,第6列空着。如果A
, B ,
C , D四个因素所有的交互作用都要考虑,则不能用
,第6列空着。如果A
, B ,
C , D四个因素所有的交互作用都要考虑,则不能用![]() ,应选用更大的正交表,如
,应选用更大的正交表,如![]() 。
。
[正交表的直观分析] 1° 计算第i水平的水平和Ki与水平均值ki例如用![]() 安排的四因素3水平的试验方案,可列出直观分析表如下:
安排的四因素3水平的试验方案,可列出直观分析表如下:
|
列号(因素) 试验号 |
1(A) 2(B) 3(C) 4(D) |
试验指标y |
|
1 2 3 4 5 6 7 8 9 |
1 1 1 1 1 2 2 2 1 3 3 3 2 1 2 3 2 2 3 1 2 3 1 2 3 1 3 2 3 2 1 3 3 3 2 1 |
y1 y2 y3 y4 y5 y6 y7 y8 y9 |
|
K1 K3 |
|
|
|
k1 k2 k3 |
|
|
|
极差R |
R(1) R(2) R(3) R(4) |
其中
![]() 表示第j列的i水平的试验指标和(简称水平和)
表示第j列的i水平的试验指标和(简称水平和)
![]() 表示第j列的i水平的试验指标均值(简称水平均值)
表示第j列的i水平的试验指标均值(简称水平均值)
![]() 表示第j列的
表示第j列的![]() 的极差
的极差
例如
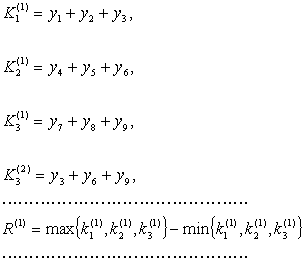
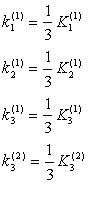
2° 评定因素重要性顺序 依照各因素指标均值的极差的大小排出重要性顺序,极差大的表示该因素重要。
3°
画出各因素与试验指标的关系图 求出![]() 后,对于每个j以水平值i横坐标,以ki为纵坐标描点并画出折线图,称为第j个因素与试验指标的关系图。若ki变化幅度大,则对应的因素的影响就愈大。若图上描出的点很分散,则说明该因素是主要的;若点比较集中,则说明该因素是次要的。
后,对于每个j以水平值i横坐标,以ki为纵坐标描点并画出折线图,称为第j个因素与试验指标的关系图。若ki变化幅度大,则对应的因素的影响就愈大。若图上描出的点很分散,则说明该因素是主要的;若点比较集中,则说明该因素是次要的。
当需要考虑因素的交互作用时,对应某交互作用的ki列的就表示由于该交互作用的影响而引起的。同样可以画出因素之间的交互作用与试验指标的关系图。
对于既没有安排因素,也没有安排交互作用的“空列”,可以用来安排试验误差的估计。通过同样的计算得到ki,这可以看作是由于试验误差造成的,ki变化的大小反映了该试验误差的大小。也可以画出实验误差与试验指标的关系图。
4° 选定最优工艺条件(最优搭配方案) 在不考虑交互作用时,只需根据该试验指标的要求(即该指标是高者为优,或是低者为优),从每个因素的关系图中找出最优点(最高点或最低点)的水平,将各因素的最优水平组合起来就是对于该指标的最优工艺条件。
当需要考虑因素间的交互作用时,经过分析已知某两个因素的交互作用对试验指标影响很大,这时根据试验结果,把对应于该二因素所有不同水平组合的试验指标(若对于同一种组合有多次试验,则应求出其平均值)进行比较,选出该二因素的最优水平组合。最后,结合其他因素或交互作用选出的最优条件综合考虑,以确定最优工艺条件。
对于多指标的试验,每个指标都可按上述方法进行分析。最优工艺条件应根据各个指标的情况综合考虑才能确定。
[正交表的方差分析] 设在正交表中因素A被安排在第j列,该列的水平数为bj(或bA),每个水平的重复数为rj,试验次数为n(行数)(显然有rjbj=n),则因素A的平方和SA(或称为第j列平方和Sj)为
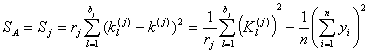
总平方和![]() 为
为
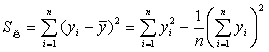
不可忽略的交互作用的平方和![]() 也按其所在列的平方和计算(公式同因素A的平方和SA的计算公式)。
也按其所在列的平方和计算(公式同因素A的平方和SA的计算公式)。
误差平方和![]() 等于
等于![]() 与所有安排有因素或交互作用的列的平方和
与所有安排有因素或交互作用的列的平方和![]() 之差,即
之差,即
![]()
正交表的方差分析表
|
离差 来源 |
平方和 |
自 由 度 |
均 方 |
统 计 量 |
置 信 限 |
统计推断 |
AB
误差 |
SA SB
|
bA – 1 bB – 1
n误 |
|
|
|
当 当 |
|
总平 方和 |
|
n |
表中
![]()
对正交表进行方差分析可以定量地给出因素的主次关系,可以判断哪些因素是重要因素,哪些因素是次要因素。此时最优工艺条件的确定只要考虑重要因素,至于那些次要因素的水平,可根据其他条件确定。