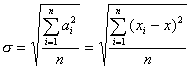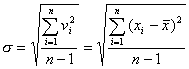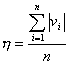三、误差的表示法
设![]() 是某观测对象的一组观测数据。其算术平均值
是某观测对象的一组观测数据。其算术平均值
![]()
误差![]() ,离差
,离差![]() ,真值对平均值的误差
,真值对平均值的误差![]() 。
。
|
名称与记号 |
定义与表示法 |
特 点 |
|
[标准误差] (中误差或均方误差)
|
各个误差平方和的平均值的平方根,即
当观测次数较大时
显然 |
不取决于观测中个别误差的符号,对观测值中的较大误差或较小误差感觉比较灵敏,是表示精密度的较好方法 |
|
[平均误差]
|
离差的绝对值的算术平均值
|
优点是计算简单,缺点是无法表示出各次观测间彼此符合的情况。例如一组观测中偏差彼此接近,而另一组观测中偏差有大中小三种。但在这两组不同的观测中所得平均误差可能相同。所以只有当n很大时才较可靠 |
|
[概率误差]
|
它是这样一个数,绝对值比它大的误差和绝对值比它小的误差出现的可能性一样大,即
|
将误差按绝对值的大小顺序排列后,序列的中位数就是概率误差。 按排列方式来求概率误差,在工作上比较困难,同时只有当n的值很大时才较可靠。 |
[标准误差、平均误差、概率误差三者关系]
![]()
![]()
![]()
![]()