四 三次样条(Spline)内插公式
样条函数是逼近函数的一种方法。
[三次样条函数] 已知平面上的n个点![]()
![]() ,这些点称为型值点,其中
,这些点称为型值点,其中![]() 称为节点。
称为节点。
如果函数S(x)满足以下三个条件:
(i)![]() ;
;
(ii)S(x)在每个区间![]() 上是一个三次多项式;
上是一个三次多项式;
(iii)S(x)在整个区间![]() 上有连续的一阶及二阶导数;
上有连续的一阶及二阶导数;
则称S(x)为过n个点的三次样条函数。
如果函数S(x)满足下面的任一边界条件(在![]() 两端点处附加的条件),那末三次样条函数S(x)存在而且唯一∶
两端点处附加的条件),那末三次样条函数S(x)存在而且唯一∶
(a)
函数在区间![]() 两端点的一阶导数(单边导数)已知,即
两端点的一阶导数(单边导数)已知,即![]()
![]() 和
和![]() 为已知数。
为已知数。
(b)
函数在区间![]() 两端点的二阶导数为零,即
两端点的二阶导数为零,即![]() 。
。
(c)
函数为周期的,且满足![]() 。
。
[三次样条函数的表达形式]
![]() 以二阶导数为参数的形式 S(x)在每个区间
以二阶导数为参数的形式 S(x)在每个区间![]() 上表为
上表为
![]()
![]()
式中![]() 为待定参数,而
为待定参数,而![]() 是
是![]() 的一阶差商,
的一阶差商,![]() 是
是![]() 的一阶差商,即
的一阶差商,即
![]()
![]()
![]()
![]()
这样定义的函数S(x)在区间![]() 上满足条件(i),(ii)。如果选择
上满足条件(i),(ii)。如果选择![]() 使得S(x)在
使得S(x)在![]() 上有一阶连续导数,那末S(x)在
上有一阶连续导数,那末S(x)在![]() 上就有二阶连续导数,而且
上就有二阶连续导数,而且
![]()
![]()
利用S(x)一阶导数的连续性及边界条件可以给出确定![]()
![]() 的代数方程组。
的代数方程组。
(1)边界条件为(a)的情况
在条件(a)下,![]()
![]() 由下面方程组解出
由下面方程组解出
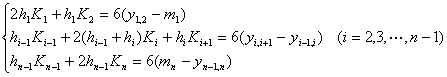
式中![]() 为一阶差商(同前),
为一阶差商(同前),![]() 和
和![]() 为给定的边界条件。
为给定的边界条件。
用矩阵表示就是
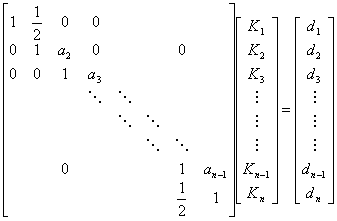
式中
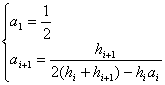
![]()
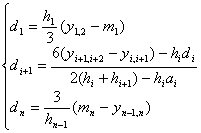
![]()
当![]()
![]() 时,解出
时,解出![]()
![]() 为
为
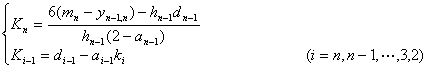
(2)边界条件为(b)的情况
在条件(b)下,![]() 由下面方程组解出:
由下面方程组解出:
![]()
![]()
用矩阵表示就是
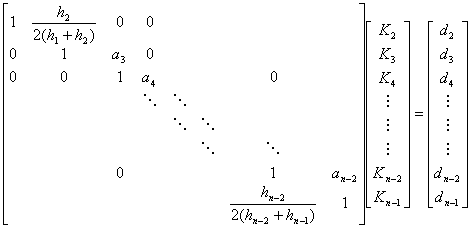
式中
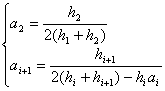
![]()
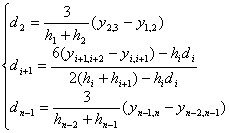
![]()
当![]()
![]() 时,解出
时,解出![]()
![]() 为
为
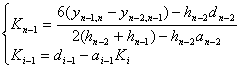
![]()
![]() 以一阶导数为参数的形式S(x)在每个区间
以一阶导数为参数的形式S(x)在每个区间![]() 上表为
上表为
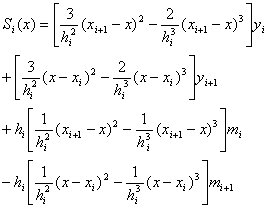
式中![]() 是待定参数。这样定义的函数S(x)在区间
是待定参数。这样定义的函数S(x)在区间![]() 上满足三次样条函数的条件(i)和(ii),而且S(x)在
上满足三次样条函数的条件(i)和(ii),而且S(x)在![]() 上有连续的一阶导数,同时
上有连续的一阶导数,同时
![]()
![]()
![]() 有时表成下式∶
有时表成下式∶
![]()
式中![]() ,而
,而![]() 与
与![]() 定义同前。
定义同前。
根据![]() 在
在![]() 上有连续二阶导数及边界条件可以给出确定
上有连续二阶导数及边界条件可以给出确定![]() 的代数方程组。
的代数方程组。
(1)
边界条件为![]() 的情况
的情况
在条件![]() 下,
下,![]() 满足下面方程组
满足下面方程组
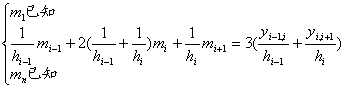
![]()
记 ![]() ,得
,得
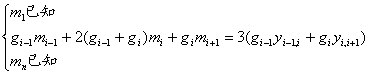
![]()
它可以改写为
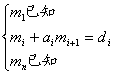
![]()
其中
![]()
![]()
![]()
![]()
![]()
由此得
![]()
![]()
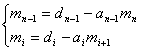
![]()
(2)边界条件为(b)的情况
在条件(b)下,![]() 满足下面方程组
满足下面方程组
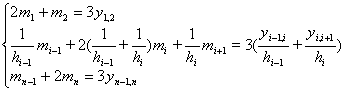
![]()
式中![]() 为
为![]() 的一阶差商。
的一阶差商。
当![]() 且
且![]()
![]() 时,
时,
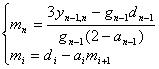
![]()
其中![]() ,而
,而![]() 由下述公式递归求得
由下述公式递归求得
![]()
![]()
![]()
![]()
![]()
![]()
(3)边界条件为(c)的情况
在条件(c)下,![]() 满足下面方程组:
满足下面方程组:
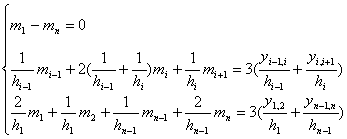
![]()