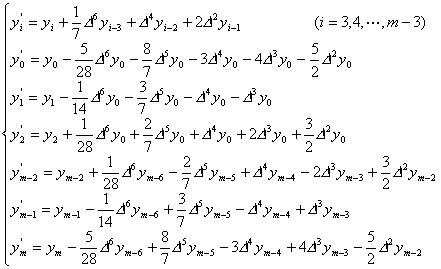二、直线的滑动平均法

对自变量x按等距作实验观测得数据如下:

x	…        …
y	…                 …

令，上述数据变为

t	-i        …       0    1    …
	…            …

    用下面的方法修正的值:取定正整数n，使至少有一个成立。当及同时成立时，选取使得

             

由此得

                 

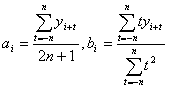
于是得时的修正公式

                 

当不同时成立时，则选取，使得

                 

式中t取[0,m]中最靠近i的2n+1个整数值。对这2n+1个t值，也得到修正公式

                  

特别在以上两种情况下，都令t=0，得到的修正值

                 

例如取n=1.当时

              

而当i=0时，应取满足

              

求出

                  

当i=m时，通过变换，可知应取

                  

[取三点滑动平均]   (即n=1)

                  

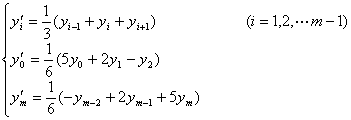
[取五点滑动平均]   (即n=2)

                 

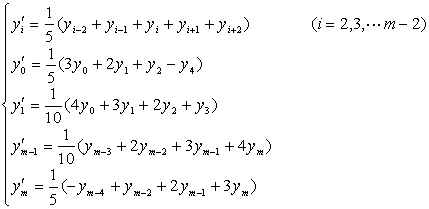
[取七点滑动平均]    (即n=3)

           

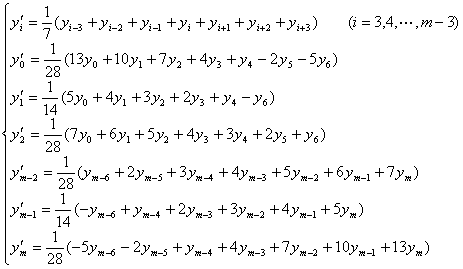
上述修正值也可用差分表示。先按本章§2的方法作差分表

x	Y

那末的修正值用差分表示为

    (i)  当n=1(即取三点滑动平均)时，

                       

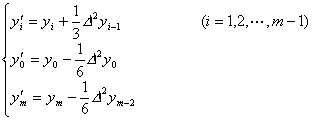
    (ii) 当n=2(即取五点滑动平均)时，

          

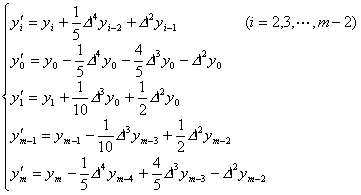
 (iii)当n=3(即取七点滑动平均)时，