§5   滤   波

从包含着误差(意味着干扰、噪声)的数据(或信号)中提取需要的信息，这种数据处理方法称为滤波。下面仅介绍几种最小二乘(或最小方差)滤波。

一、最小二乘滤波

   [增长记忆的最小二乘滤波]

   滤波的最小二乘准则

 给定离散观测系统

              

式中

              

              

              

            

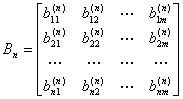
式中表示转置，是在时刻的观测值，是由形成的n维列矢量，称为观测矢量；是的矩阵，其中m是常数；是n维列矢量，它的分量是时的误差；是状态矢量(m维)。假设状态满足方程

                 

其中为m阶方阵，其元素均为常数，又设可逆，记。

如果当时

            

则称是的在最小二乘意义下的最优估值。

假设可逆，记，于是可以推出

                    

  滤波的递推公式

    上述求的最优估值的公式在电子计算机上并不实用，通常在计算机上用递推公式。可以推出

             

其中

       

是m维行矢量

                 

满足。

从以上公式来看，为求，实际上用到了全部历史观测值，随着n增大，用到的个数增多，故这种滤波递推公式称为增长记忆的。

[加权最小二乘滤波]  当n充分大时，较早的历史数据用在估计中往往起不利的作用，通过加权处理，可以使“过老”数据的作用逐渐消失。下面举加“指数下降”权的例。

选取，引进对角线矩阵序列

          

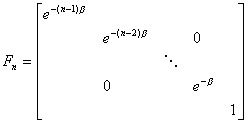
同前，设观测系统与状态方程分别为

                   

                      

如果时

         

则称是在加“指数下降”权最小二乘意义下的最优估值。

可以证明

           

其中

               

    并且有计算的递推公式

              

其中

     

是m维行矢量，定义同前面一样。