§3  同余式

    [同余及其性质]  设m为自然数,若整数a与b之差a-b为m的倍数,则称a与b对模m同余,记做

    (mod m)

否则记为

   (mod m)

表示a与b对模m不同余.

    同余具有下列性质:

    1°  (mod m)                               (自反性)

    2°  若(mod m),则(mod m)               (对称性)

    3°  若,(mod m),则(mod m)          (传递性)

    4°  若,(mod m),则

          (mod m)

          (mod m)

             (mod m)

    5°  若,(mod m),且,则(mod m).

    [完全剩余系与缩剩余系]  设以m为模,则由同余性质1°,2°,3°可将全体整数分为m个类,同类的数都同余,不同类的数不同余,称这样的类为同余类,每类中各取一数为代表,例如

构成一个完全剩余系.

    在与m互素的各类中取一代表

构成一缩剩余系(简称缩系),此处j (m)为不超过m且与m互素的数的个数(称为欧拉函数).

    剩余系具有下列性质:

    1°  若, x过m的一完全剩余系,过的一完全剩余系,则过的一完全剩余系.

    2°  若, x过m的一缩系, 过的一缩系,则过的一缩系.

    3°  若为模m的一缩系,且(k,m)=1,则

          

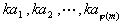
也为m的一缩系

    [欧拉定理]  若(k,m)=1,则

(mod m)

式中j (m)为欧拉函数.

    [费马定理]  若p为素数,则对所有整数a, 有

(mod p)

    显然费马定理是欧拉定理的特例.

    [一次同余方程可解条件]  同余方程

(modm)

有解的充分必要条件是:

                            

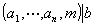
当满足此条件时,其解数(对模m的不同余者)为

                            

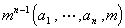
    [一元一次同余方程的解法]  一元一次同余方程

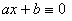           (modm)                                      (1)

有解的充分必要条件是:,若有解则共有(a,m)个互不同余的解,modm.解法如下:

    设(a,m)=d,,则原方程(1)化为

记作

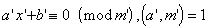                                     (2)

    首先由辗转相除法确定(见§1),使得

则

是同余方程(2)的解,最后得到

x=x’+m’t , t=

为原方程(1)的解,mod m.即有d个解

对模m不同余.

    [孙子定理*] 若，i≠j，则同余方程组

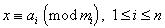                                         (3)

有唯一解, .

    同余方程组(3)的解法如下:

    因为,所以可由辗转相除法求出,满足

    记

于是

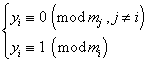
    最后计算

它就是同余方程组(3)的唯一解,.

    [二次剩余与二次非剩余]  设m为大于1的整数,(n,m)=1,若

  (mod m)

可解,则称n为对模m的二次剩余,或二次剩余,mod m.否则,称n为对模m的二次非剩余.

    两个二次剩余之积仍为二次剩余,mod p.

    两个二次非剩余之积为二次剩余,mod p.

    一个二次剩余与一个二次非剩余之积为一个二次非剩余,mod p.

    设p为奇素数,则在模p的缩剩余系中,有个二次剩余:

有个二次非剩余, mod p.

    [勒让德符号及其性质]  设p为奇素数,pn又设

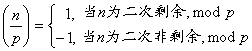
则称为勒让德符号.

    勒让德符号具有下列性质:

    1°  若(mod p), pn则

=

    2°  欧拉判别条件: 设p为奇素数,则

 (mod p)

    3°  若p为奇素数, pmn ,则

    4°  若p为奇素数,则

    5°  若p为奇素数,则

    6°  高斯互逆定律: 设p,q为两个不同的奇素数,则

    [二次同余式的解数]  设l>0, pn,若p为奇素数，则二次同余式

  (mod )

的解数为.

    当p=2时,l=1时 有一解.

                        

    [对模m的次数]  设h为一整数,(m,h)=1,满足

(mod m)

的最小正整数l称为h对模m的次数,或h的次数,mod m.

    若(mod m),则,这里l为h的次数,mod m

    [素数模的原根与指数]  设p为素数,次数为p－1的数称为模p的原根.

    设g为模p的一原根,则

两两互不同余.

    任一整数n( pn),必有一数a使得

  (modp)  ,

此a称为n的指数,mod p.记作

                               

在不易混淆时,简记indn.

    指数具有下列性质:

    1°  若b为满足

                               (mod p)

的任一数,则

                             (mod p－1)

    2°  (mod p－1), pab

    3°  (mod p－1), pa

    4°  底数互换公式 设,为模p的两个不等的原根,且(mod p),则

(mod p－1)

    [模m的原根]  设m为一自然数,若有一数g存在,使得

                           (mod m)

两两互不同余,则此g称为对模m的原根, 模m的原根存在的充分必要条件是:

(p为奇素数,l为正整数)

    [素数及其最小原根表(5000以内)]  加*者表示10为其原根

p

g

p

g

p

g

p

g

3

5

7*

11

13

17*

19*

23*

29*

31

37

41

43

47*

53

59*

61*

67

71

73

79

83

89

97*

101

103

107

109*

113*

127

131*

137

139

149*

151

157

163

167*

173

179*

181*

191

193*

197

199

211

223*

227

229*

233*

239

241

2

2

3

2

2

3

2

5

2

3

2

6

3

5

2

2

2

2

7

5

3

2

3

5

2

5

2

6

3

3

2

3

2

2

6

5

2

5

2

2

2

19

5

2

3

2

3

2

6

3

7

7

251

257*

263*

269*

271

277

281

283

293

307

311

313*

317

331

337*

347

349

353

359

367*

373

379*

383*

389*

397

401

409

419*

421

431

433*

439

443

449

457

461*

463

467

479

487*

491*

499*

503*

509*

521

523

541*

547

557

563

569

571*

6

3

5

2

6

5

3

3

2

5

17

10

2

3

10

2

2

3

7

6

2

2

5

2

5

3

21

2

2

7

5

15

2

3

13

2

3

2

13

3

2

7

5

2

3

2

2

2

2

2

3

3

577*

587

593*

599

601

607

613

617

619*

631

641

643

647*

653

659*

661

673

677

683

691

701*

709*

719

727*

733

739

743*

751

757

761

769

773

787

797

809

811*

821*

823*

827

829

839

853

857*

859

863*

877

881

883

887*

907

911

919

5

2

3

7

7

3

2

3

2

3

3

11

5

2

2

2

5

2

5

3

2

2

11

5

6

3

5

3

2

6

11

2

2

2

3

3

2

3

2

2

11

2

3

2

5

2

3

2

5

2

17

7

929

937*

941*

947

953*

967

971*

977*

983*

991

997

1009

1013

1019*

1021*

1031

1033*

1039

1049

1051*

1061

1063*

1069*

1087*

1091*

1093

1097*

1103*

1109*

1117

1123

1129

1151

1153*

1163

1171*

1181*

1187

1193*

1201

1213*

1217*

1223*

1229*

1231

1237

1249

1259*

1277

1279

1283

1289

3

5

2

2

3

5

6

3

5

6

7

11

3

2

10

14

5

3

3

7

2

3

6

3

2

5

3

5

2

2

2

11

17

5

5

2

7

2

3

11

2

3

5

2

3

2

7

2

2

3

2

6

p

g

p

g

p

g

p

g

1291*

1297*

1301*

1303*

1307

1319

1321

1327*

1361

1367*

1373

1381*

1399

1409

1423

1427

1429*

1433*

1439

1447*

1451

1453

1459

1471

1481

1483

1487*

1489

1493

1499

1511

1523

1531*

1543*

1549*

1553*

1559

1567*

1571*

1579*

1583*

1597

1601

1607*

1609

1613

1619*

1621*

1627

1637

1657

1663*

p

2

10

2

6

2

13

13

3

3

5

2

2

13

3

3

2

6

3

7

3

2

2

5

6

3

2

5

14

2

2

11

2

2

5

2

3

19

3

2

3

5

11

3

5

7

3

2

2

3

2

11

3

g

1667

1669

1693

1697*

1699

1709*

1721

1723

1733

1741*

1747

1753

1759

1777*

1783*

1787

1789*

1801

1811*

1823*

1831

1847*

1861*

1867

1871

1873*

1877

1879

1889

1901

1907

1913*

1931

1933

1949*

1951

1973

1979*

1987

1993*

1997

1999

2003

2011

2017*

2027

2029*

2039

2053

2063*

2069*

2081

p

2

2

2

3

3

3

3

3

2

2

2

7

6

5

10

2

6

11

6

5

3

5

2

2

14

10

2

6

3

2

2

3

2

5

2

3

2

2

2

5

2

3

5

3

5

2

2

7

2

5

2

3

g

2083

2087

2089

2099*

2111

2113*

2129

2131

2137*

2141*

2143*

2153*

2161

2179*

2203

2207*

2213

2221*

2237

2239

2243

2251*

2267

2269*

2273*

2281

2287

2293

2297*

2309*

2311

2333

2339*

2341*

2347

2351

2357

2371*

2377

2381

2383*

2389*

2393

2399

2411*

2417*

2423*

2437*

2441

2447*

2459*

2467

p

2

5

7

2

7

5

3

2

10

2

3

3

23

7

5

5

2

2

2

3

2

7

2

2

3

7

19

2

5

2

3

2

2

7

3

13

2

2

5

3

5

2

3

11

6

3

5

2

6

5

2

2

g

2473*

2477

2503

2521

2531

2539*

2543*

2549*

2551

2557

2579*

2591

2593*

2609

2617*

2621*

2633*

2647

2657*

2659

2663*

2671

2677

2683

2687*

2689

2693

2699*

2707

2711

2713*

2719

2729*

2731

2741*

2749

2753*

2767*

2777*

2789*

2791

2797

2801

2803

2819*

2833*

2837

2843

2851*

2857

2861*

2879

p

5

2

3

17

2

2

5

2

6

2

2

7

7

3

5

2

3

3

3

2

5

7

2

2

5

19

2

2

2

7

5

3

3

3

2

6

3

3

3

2

6

2

3

2

2

5

2

2

2

11

2

7

g

2887

2897*

2903*

2909*

2917

2927*

2939*

2953

2957

2963

2969

2971*

2999

3001

3011*

3019*

3023*

3037

3041

3049

3061

3067

3079

3083

3089

3109

3119

3121

3137*

3163

3167*

3169

3181

3187

3191

3203

3209

3217

3221*

3229

3251*

3253

3257*

3259*

3271

3299*

3301*

3307

3313*

3319

3323

3329

3331*

p

5

3

5

2

5

5

2

13

2

2

3

10

17

14

2

2

5

2

3

11

6

2

6

2

3

6

7

7

3

3

5

7

7

2

11

2

3

5

10

6

6

2

3

3

3

2

6

2

10

6

2

3

3

g

3343*

3347

3359

3361

3371*

3373

3389*

3391

3407*

3413

3433*

3449

3457

3461*

3463*

3467

3469*

3491

3499

3511

3517

3527*

3529

3533

3539*

3541

3547

3557

3559

3571*

3581*

3583

3593*

3607*

3613

3617*

3623*

3631

3637

3643

3659*

3671

3673*

3677

3691

3697

3701*

3709*

3719

3727*

3733

3739

3761

p

5

2

11

22

2

5

3

3

5

2

5

3

7

2

3

2

2

2

2

7

2

5

17

2

2

7

2

2

3

2

2

3

3

5

2

3

5

21

2

2

2

13

5

2

2

5

2

2

7

3

2

7

3

g

3767

3769

3779*

3793

3797

3803

3821*

3823

3833*

3847*

3851*

3853

3863*

3877

3881

3889

3907

3911

3917

3919

3923

3929

3931

3943*

3947

3967*

3989*

4001

4003

4007*

4013

4019*

4021

4027

4049

4051*

4057*

4073*

4079

4091*

4093

4099

4111

4127

4129

4133

4139*

4153*

4157

4159

4177*

4201

4211*

p

5

7

2

5

2

2

3

3

3

5

2

2

5

2

13

11

2

13

2

3

2

3

2

3

2

6

2

3

2

5

2

2

2

3

3

10

5

3

11

2

2

2

17

5

13

2

2

5

2

3

5

11

6

g

4217*

4219*

4229*

4231

4241

4243

4253

4259*

4261*

4271

4273

4283

4289

4297

4327*

4337*

4339*

4349*

4357

4363

4373

4391

4397

4409

4421*

4423*

4441

4447*

4451*

4457*

4463*

4481

4483

4493

4507

4513

4517

4519

4523

4547

4549

4561

4567*

4583*

4591

4597

4603

4621

4637

4639

4643

4649

4651*

p

3

2

2

3

3

2

2

2

2

7

5

2

3

5

3

3

10

2

2

2

2

14

2

3

3

3

21

3

2

3

5

3

2

2

2

7

2

3

5

2

6

11

3

5

11

5

2

2

2

3

5

3

3

g

4657

4663

4673*

4679

4691*

4703*

4721

4723

4729

4733

15

3

3

11

2

5

6

2

17

5

4751

4759

4783*

4787

4789

4793*

4799

4801

4813

4817*

19

3

6

2

2

3

7

7

2

3

4831

4861

4871

4877

4889

4903

4909

4919

4931*

4933

3

11

11

2

3

3

6

13

6

2

4937*

4943*

4951

4957

4967*

4969

4973

4987

4993

4999

3

7

6

2

5

11

2

2

5

3

* 外国书刊中称孙子定理为中国剩余定理。我国古代在《孙子算经》“物不知其数”一问中对此类问题的解法已作叙述。