三、  公理系统规定的集

    [子集] 假定A和B都是集,B的每个元素都是A的元素,那末称B为A的一个子集,记作BA或AB.“”读作“包含于”或“被掩于”，“”读作“包含”或“掩盖”.

    对于任何的集A,B和C有

1°  AA                        (自反律)

2°  从AB,BA,可推出A=B   (反对称律)

3°  若AB,BC,则AC        (传递律)

    假定BA但是BA(B=A不成立),那末称B为A的一个真子集,记作(BA).

    规定空集是任何集的子集.

    [变进的变换] 假定一个变换f把一个集X变上集Y的一个子集,那末称f为把X变进Y的变换,简称f是变进的(映入的).变上是变进的特殊情况.

    [划分公理与特征函数] 假定有一个变换f把一个集X变进{0,1},那末1的所有象源的全体是X的一个子集X',f称为X'的特征函数.

    划分公理是替换公理的结论,因为如果1的象源全体是φ,那末φ当然是X的子集,否则1至少有一个象源x₀X,造一个变换

 

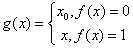
那末g(X)=X',所以X是集.

    推论  假定X是集,对每个xX,论点p(x)和­(p(x)的否定)一定有一个且只有一个成立,那末{x|xX且p(x)}是一个集.

    [差集与余集] 假定A和B都是集,那末所有属于A但不属于B的元素的全体是一个集(由划分公理的推论),称为A和B的差集记作A\B.

    特别,当BA的时候,A\B称为B在A中的余集.

    [方幂集公理] 一个集A的所有子集的全体是一个集,记作,称为A方幂集.

    可以把一对一地变上“所有把A变进2 = {0，1}的变换的全体”去，所以后者也是一个集，这个集和A方幂集可以互相作为彼此的标号集.今后,往往把它们看作同一个集,也就是把A的一个子集跟它的一个特征函数混同起来.

    [和集(并)与和集公理] 假定{A_h|hH}是一个集族,那末{x|存在一个A_hx}是一个集,它称为这族集的和集(并),记作.

    当一个集族的全部集是A,B,C,…时,这族集的和集可写成

                             A∪B∪C∪ …

    例     {1,2,3}∪{0,2,4}∪{2,1}={0,1,2,3,4}

    [通集(交)] 假定{A_h|hH}是一个集族,那末{x|所有的A_hx}是一个集,它称为这族集的通集(交),记作.通集存在是划分公理的结论.

    当一个集族的全部集是A,B,C,…时,这族集的通集可写成

                         A∩B∩C∩…

    例     {1,2,3}∩{0,2,4}∩{2,1}={2}

    [直接积(笛卡儿积)] 假定A={x_h|hH},B={y_k|kK},那末

                     {<x_h,y_k>|x_hA且y_kB}

是一个集,它称为A和B的直接积,记作AB.

    直接积存在是替换公理与和集公理的结论.因为对任何hH与kK,{<x_h,y_k>}是一个集,由替换公理,{{<x_h,y_k>}|hH}是一个集族,因此存在和集.{C_k|kK}又是一个集族,所以又存在和集,这就是AB.

    假定{A_h|hH }是一个集族,其中每个A_h ¹φ那末由选择公理(§2,一)对每个hH可以得到一个x_hA_h,并且由替换公理得到一个集

<x_h|hH>={{ x_h ,h}|hH}

称为由一个选择变换(§2,四)得到的有序组.

    把每个x_hA_h 换为一个x^'_h A_h ,那末由替换公理得到另一个集

<x^'_h|hH>={{ x^'_h ,h}|hH}

这同样可以看作由一个选择变换得到的有序组.

    所有这种有序组的全体是一个集，它称为一族集A_h(hH)的直接积,记作.

    H=2时,就是AB.

    [叠集] 假定A和B都是集,那末由变换的定义,每个把A变进B的变换f都是AB的子集,因此f.由划分公理,所有把A变进B的变换f的全体{f|f且f把A变进B}是一个集,称为把A叠在B上的叠集,记作^AB.

    显然, ^AB.另一方面,特别当B=2={0,1}时,^A2既是方幂集又是叠集.

    [集的运算规律] 设A,B,C都是集,则

    交换律        A∪B=B∪A,A∩B=B∩A

    结合律        A∪(B∪C)=(Α∪B)∪C

A∩(Β∩C)=(Α∩B)∩C

    分配律        A∩(B∪C)=(A∩B)∪(A∩C)

A∪(B∩C)=(A∪B)∩(A∪C)

    德×摩根(De Morgan)律

              C\(A∪B)=(C\A)∩(C\B)

              C\(A∩B)=(C\A)∪(C\B)