三、    拓扑空间的分离程度·可数公理

1.      不同分离程度的拓扑空间

    [T₀空间]  如果拓扑空间X里任何不同的两点中至少有一点有一个邻域不包含另一点，那末称X为T₀空间.

    [T₁空间]  如果拓扑空间X里任何不同的两点一定各有邻域不包含另一点，那末称X为T₁空间.

    X是T₁空间的充分必要条件是：X里任何一个只包含一点x的集{x}是闭集.

    [T₂空间——豪斯道夫空间]  如果拓扑空间X里任何不同的两点一定各有邻域彼此没有公共点，那末称X为T₂空间，也称分离空间.

    [正则空间]  假定对拓扑空间X里任何一个闭集S和任何一点xÏS，一定有两个开集U和V，使UÊS，Vx且U∩V¹φ，那末称X为正则空间.

    [T₃的空间]  正则的T₁空间称为T₃空间.

    [正常空间]  假定对拓扑空间X里任何两个没有公共点的闭集A和B一定有两个开集U和V使UÊA,VÊB且U∩V=φ，那末称X为正常空间.

    [T₄空间]  正常的T₁空间称为T₄空间.

    例如n维实数空间就是T₄空间.

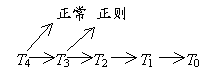
    定义所说的分离程度强弱次序如下：

    箭头表示“必是”.如T₄空间必是T₃空间，又必是正常空间.至于正常和正则是不能比较分离强弱程度的，它们跟T₂ ,T₁与T₀也是不能比较的.