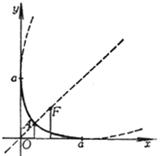
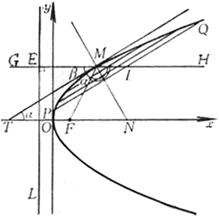
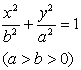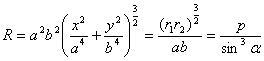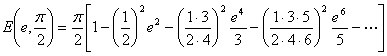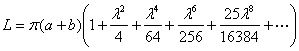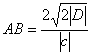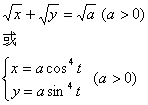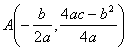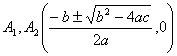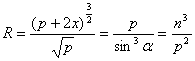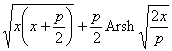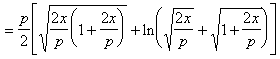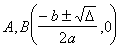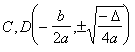§ 5 二次曲线
一、 圆
[圆的方程、圆心与半径]
|
方 程 与 图 形 |
圆 心 与 半 径 |
|
|
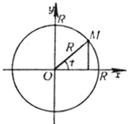
x2 + y2 = R2 或 (参数方程,t为动径OM与x轴正方向的夹角)
|
|
圆心 G(0,0) 半径 r = R
|
|
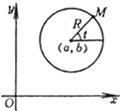
(x - a)2+(y - b)2 = R2 或 (参数方程,t为动径OM与x轴正方向的夹角) |
|
圆心 G(a, b) 半径 r = R
|
|
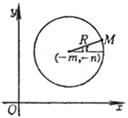
x2 + y2 + 2mx + 2ny + q = 0 m2 + n2 > q r2 + 2r (mcost + nsint) + q = 0 (极坐标方程)
|
|
圆心 G(-m,-n) 半径
|
|
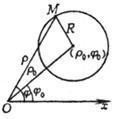
r2 - 2rr0cos(j - j0) + r02 = R2 (极坐标方程)
|
|
圆心 G(r0,j0) 半径 r = R
|
|
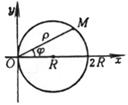
x2 + y2 = 2Rx 或 r = 2Rcosj (极坐标方程) |
|
圆心 G(R, 0) 半径 r = R
|
|
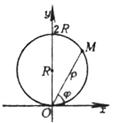
x2 + y2 = 2Ry 或 r = 2Rsinj (极坐标方程) |
|
圆心 G(0,R) 半径 r = R |
[圆的切线]
圆 x2 + y2 = R2 上一点M(x0, y0)的切线方程为
x0x + y0y = R2
圆 x2 + y2 + 2mx + 2ny + q = 0 上一点M(x0, y0)的切线方程为
x0x + y0y + m(x + x0) + n(y + y0) + q = 0
[两个圆的交角、圆束与根轴]
|
方 程 与 图 形 |
公 式 与 说 明 |
|
两个圆的交角 C1 x2 + y2 + 2m1x + 2n1y + q1 = 0 C2 x2 + y2 + 2m2x + 2n2y + q2 = 0 两个圆的交角是指它们在交点的两条切线的夹角
|
式中q表示两个圆C1和C2的交角,因为公式中不包含交点的坐标,所以在两交点的两交角必相等. 两个圆C1和C2正交条件为 2m1m2 + 2n1n2 - q1 - q2 = 0
|
|
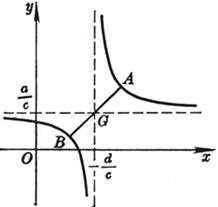
圆束×两个圆的根轴 Cl C1 + lC2 = 0 (l为参数) 或 (l + 1)(x2 + y2) + 2(m1 + lm2)x + 2(n1+ln2)y + (q1 + lq2) = 0 根轴方程为 2(m1 - m2)x + 2(n1 - n2)y + (q1 - q2) = 0
|
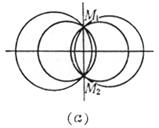
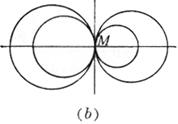
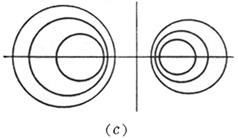
对l(l ¹ -1)的一个确定值,Cl表示一个圆.当l取一切值(l ¹ -1)时,Cl所表示的圆的全体,称为圆束.l = -1时,为一直线,称为两个圆C1和C2的根轴.根轴与C1和C2的连心线垂直,束中任一圆Cl的圆心在C1和C2的连心线上,且分连心线的比等于l. (a)如果C1和C2 相交于两点M1,M2,则束中一切圆都通过两交点M1,M2,它们的根轴就是它们的公共弦.这时圆束称为共轴圆系(图(a)). (b)如果C1和C2切于一点M,则束中一切圆都在一点M相切,根轴就是在点M的公切线(图(b)). (c)如果C1和C2不相交,则束中一切圆都不相交,根轴也与圆束中一切圆都不相交(图(c)). 从点P作两个圆C1和C2的切线,具有相等切线长的点P的轨迹就是根轴.两个同心圆的根轴是从公共圆心到无穷远处的直线.三个圆中每对圆的根轴(共三个)交于一点,它称为根心.若三个圆心共线,则其根心在无穷远处.
|
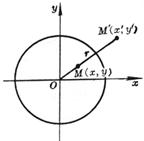
[反演] 设C为一定圆,O为圆心,r为半径(图7.1),对平面上任一点M,有一点M¢与它对应.使得满足下列两个条件:
(i)O, M, M¢共线,
(ii)OM×OM¢ = r2,
这种点M¢称为点M关于定圆C的反演点,C称为反演圆,O称为反演中心,r称为反演半径.
由于M和M¢的关系是对称的,所以M也是M¢的反演点.因r2 > 0,所以M和M¢都在O的同侧.M和M¢之间的对应称为关于定圆C的反演.
取O为原点,则一切反演点M(x, y)和M¢(x¢,y¢)的对应方程为
![]()
反演具有性质:
|
图7.1 |
1° 不通过反演中心的一条直线变为通过反演中心的一个圆.
2° 通过反演中心的圆变为不通过反演中心的直线.
3° 通过反演中心的一条直线变为它自己.
4° 不通过反演中心的圆变为不通过反演中心的圆.
5° 反演圆变为它自己.
6° 与反演圆正交的圆变为它自己,其逆也真.
7° 如果两条曲线C1,C2交于一点M,则经过反演后的曲线C1¢, C2¢必交于M的反演点M¢.
8° 如果两条曲线C1, C2在一点M相切,则经过反演后的曲线C1¢, C2¢必在M的反演点M¢相切.
9° 两条曲线的交角在反演下是不变的.由此可见,反演是一个保角变换.
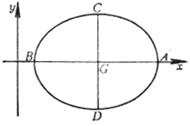
二、 椭圆
1.椭圆的基本元素
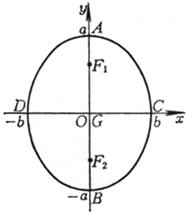
主轴(对称轴)
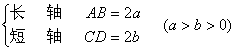
顶 点 A, B, C, D
椭圆中心 G
焦 点 F1, F2
焦
距 ![]()
离 心 率 ![]()
压缩系数 ![]()
焦点参数 ![]() (等于过焦点且垂直于长轴的弦长之半,即F1H)
(等于过焦点且垂直于长轴的弦长之半,即F1H)
焦点半径 r1, r2(椭圆上一点(x, y)到焦点的距离)
r1 = a - ex, r2 = a + ex
直 径 PQ(通过椭圆中心的弦)
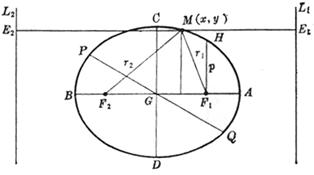
图 7.2
共轭直径 二直径斜率为![]() ,且满足
,且满足![]()
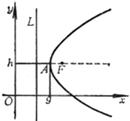
准
线 L1和L2(平行于短轴,到短轴的距离为![]() )
)
2.椭圆的方程、顶点、中心与焦点
|
方 程 与 图 形 |
顶点·中心·焦点 |
|
|
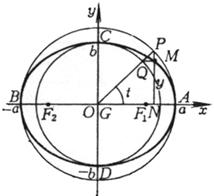
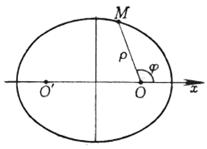
(参数方程,t为与M点对应的同心圆(半径为a, b)的半径与x轴正方向的夹角)
|
|
顶点 A, B(±a, 0) C, D(0,±b) 中心 G(0,0) 焦点 F1, F2(±c,0)
|
|
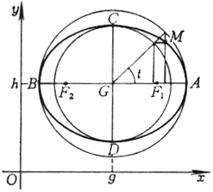
(t同上) |
|
顶点 A, B(g ± a, h) C, D(g, h ± b) 中心 G(g, h) 焦点 F1, F2(g ± c, h)
|
|
|
|
顶点 A, B(0, ± a) C, D(± b, 0) 中心 G (0, 0) 焦点 F1, F2(0, ± c)
|
|
(极坐标方程,极点位于椭圆一焦点上,极轴为从焦点指向最近一个顶点的射线,j为极角,p, e如前述) |
|
长轴 短轴 焦距
|
3.椭圆的性质
1° 椭圆是到两定点(即焦点)的距离之和为常数(即长轴)的动点M的轨迹 (r1 + r2 = 2a).
2° 椭圆也是到一定点(即焦点之一)的距离与到一定直线(即一准线L)的距离之比为小于1的常数(即离心率)的动点M的轨迹(MF1/ME1 = MF2/ME2 = e).
3° 椭圆是将半径为a的圆沿y轴方向按比![]() (即压缩系数)压缩而得到.
(即压缩系数)压缩而得到.
4° 椭圆上一点M(x0, y0)的切线(MT)方程为
![]()
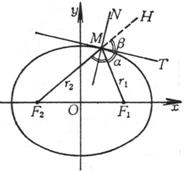
切线把点M的两焦点半径间的外角(即∠F1MH)平分(即a=b,![]() ),M点的法线MN把内角(即∠F1MF2)平分(图7.3).
),M点的法线MN把内角(即∠F1MF2)平分(图7.3).
如果椭圆的切线(MT)的斜率为k,则其方程为
![]()
|
图 7.3 |
式中正负号表示直径两端点的两切线.
|
图 7.4 |
5° 椭圆的任一直径把平行于其共轭直径的弦平分(图7.4)
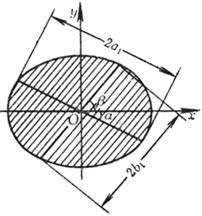
如果两共轭直径的长分别为2a1和2b1, 两直径与长轴的夹角(锐角)分别为a和b, 则 a1b1sin(a + b) = ab
a12 + b12 = a2 + b2
6° 椭圆上任一点M的焦点半径之积等于它的对应半共轭直径的平方.
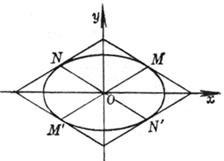
7° 设MM¢, NN¢为椭圆的两共轭直径, 通过M, M¢分别作直线平行于NN¢; 又通过N, N¢分别作直线平行于MM¢, 则这四条直线构成的平行四边形的面积为一常数4ab(图7.5).
|
图 7.5 |
4.椭圆各量计算公式
![]()
|
椭圆各量 |
计 算 公 式 |
||
|
[曲率半径] R |
式中r1, r2为焦点半径, p为焦点参数, a为点M(x, y)的焦点半径与切线的夹角.特别, 顶点的曲率半径 |
||
|
[弧长] |
式中e为离心率 |
||
|
[周长] L
|
式中, 设 |
||
|
[面积] S |
扇形(OAM)面积 弓形(MAN)面积 椭 圆 面 积 S = pab |
||
|
[几何重心] G
|
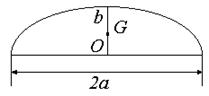
椭 圆 形 G与O重合 半椭圆形 (a, b为椭圆的半轴长) |
|
|
|
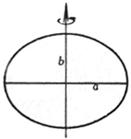
[转动惯量] J
|
椭圆的转轴通过b轴 式中m为质量 |
|
|
三、 双曲线
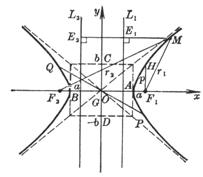
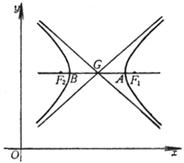
1.[1051]双曲线的基本元素
主轴(对称轴)
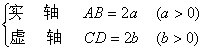
|
图 7.6 |
顶 点 A, B
中 心 G
焦 点 F1, F2
焦 距 F1F2
= 2c, ![]()
离 心 率 ![]()
焦点参数 ![]() (等于过焦点且垂直于实轴的弦长之
(等于过焦点且垂直于实轴的弦长之
半,即F1H)
焦点半径 r1, r2 (双曲线上一点(x, y)到焦点的距离,
即MF1, MF2)
r1 = ± (ex - a), r2 = ± (ex + a)
直 径 PQ(通过中心的弦)
共轭直径 二直径斜率为k, k¢,且满足![]()
准 线 L1和L2 (垂直于实轴, 到中心的距离为![]() )
)
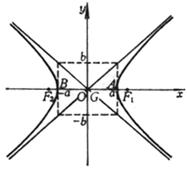
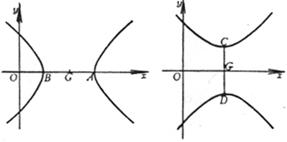
2.双曲线的方程、顶点、中心、焦点与渐进线
|
方 程 与 图 形 |
顶点·中心·焦点·渐近线 |
||
|
或
(参数方程) 或 |
|
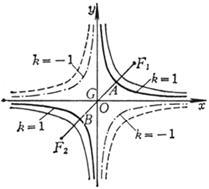
顶 点 A, B(±a,0) 中 心 G(0,0) 焦 点 F1, F2(±c,0) 渐 近 线
|
|
|
(与
|
|
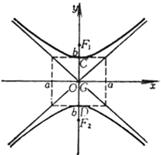
顶 点 中 心 焦 点
渐 近 线 |
|
|
|
|
顶 点
中 心 焦 点
渐 近 线
|
|
|
方 程 |
与 图 形 |
顶点·中心·焦点·渐近线 |
|
|
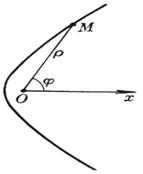
(极坐标方程.极点位于一焦点上,极轴为从焦点背向顶点的射线,p, e如前述.由此方程只能确定一支,另一支可由对称性而得到)
|
|
实 轴 虚 轴
焦 距
|
|
|
|
顶 点 中 心 焦
点 (当k>0时取同号,k<0时取异号) 轴
长 渐 近 线 |
||
|
(等轴双曲线)
|
|
顶
点 中
心 轴 长 渐 近 线
|
|
 3.双曲线的性质
3.双曲线的性质
1° 双曲线是到两定点(焦点)的距离之差为常数(等于实轴2a)的动点M的轨迹(使![]() 的各点属于双曲线的一支,而使
的各点属于双曲线的一支,而使![]() 的各点属于其另一支).
的各点属于其另一支).
2° 双曲线也是到一定点(焦点之一)的距离与到一定直线(准线L1)的距离之比为大于1的常数(即离心率)的动点M的轨迹(![]() ).
).
3° 双曲线上一点M![]() 的切线(MT)的方程为
的切线(MT)的方程为
![]()
|
图 7.8 |
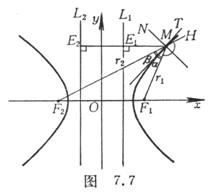
它把M点两焦点半径间的内角(即![]() )平分(即
)平分(即![]() ),而M点的法线MN把外角(即
),而M点的法线MN把外角(即![]() )平分(图7.7).
)平分(图7.7).
如果双曲线的切线的斜率为k,则其切线的方程为
![]()
式中正负号表示在直径两端点的两切线.
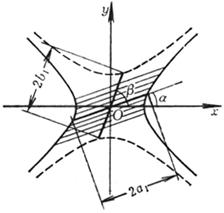
4° 两条渐近线![]() 之间的切线线段TT1被切点M平分(TM = MT1),且
之间的切线线段TT1被切点M平分(TM = MT1),且
DOTT1的面积![]() ,
,
平行四边形OJMI的面积(图7.8的阴影部分)
![]()
5° 双曲线的任一直径把平行于共轭直径的弦平分(图7.9)
|
图 7.9 |
如果两共轭直径的长分别为2a1,2b1, 两直径与实轴夹角(锐角)分别为a和b(a<b),则
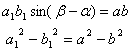
6° 双曲线上任一点M的焦点半径之积等于它的对应半共轭直径的平方.
|
图 7.10 |
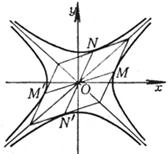
7° 设MM¢, NN¢为双曲线的两共轭直径,通过M, M¢分别作直线平行于NN¢;又通过N, N¢分别作直线平行于MM¢,则这四条直线构成的平行四边形的面积为一常数4ab(图7.10).
4.双曲线各量计算公式
|
|
![]()
|
双曲线各量 |
计 算 公 式 |
|
[曲率半径] R
|
式中r1, r2为焦点半径,p为焦点参数,a为点M(x, y)的焦点半径与切线的夹角,特别,顶点A, B的曲率半径
|
|
双曲线各量 |
计 算 公 式 |
|
[弧长]
|
式中e为离心率 |
|
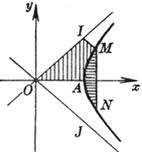
[面积] S
|
弓形(AMN)的面积: OAMI的面积: 这里OI, OJ为渐近线,MI // OJ |
四、 抛物线
|
图 7.11 |
1.抛物线的基本元素
抛物线的主轴 AB
顶 点 A
焦 点 F
焦点参数 p(等于过焦点且垂直于轴的
弦CD之长的一半)
焦点半径 MF(抛物线上一点到焦点的
距离)
直 径 EMH(平行于抛物线的轴的直
线)
准
线 L(与抛物线的轴垂直,到顶点A的距离等于![]() ,到焦点F的距离等于p)
,到焦点F的距离等于p)
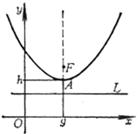
2.抛物线的方程、顶点、焦点与准线
|
方 程 与 图 形 |
顶点·焦点·准线 |
|
|
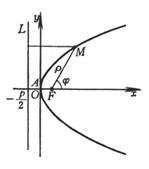
(极坐标方程,极点位于焦点F上,极轴与抛物线的轴重合,背向顶点) |
|
顶 点 A(0, 0) 焦
点 准 线 |
|
|
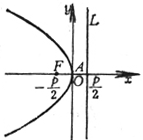
|
顶 点 A(0, 0) 焦
点 准
线
|
|
方 程 与 图 形 |
顶点·焦点·准线 |
|
|
|
|
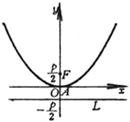
顶 点 A(0, 0) 焦
点
准 线 |
|
|
|
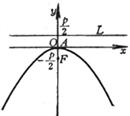
顶 点 A(0, 0) 焦
点
准 线 |
|
|
|
顶 点 A(g, h) 焦
点 准
线
|
|
|
|
顶 点 A(g, h) 焦
点
准 线 |
|
|
|
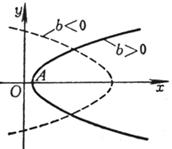
顶
点 (当a>0时,开口向上, 当a<0时,开口向下) 焦点参数 与x轴的交点
顶
点
焦点参数
|
3.抛物线的性质
|
图 7.12 |
1° 抛物线是到一定点F(焦点)的距离与到一定直线L(准线)的距离相等的动点M的轨迹(MF¢=ME)(图7.12)
2° 抛物线上一点![]() 的切线MT的方程为
的切线MT的方程为
![]()
它把M点的焦点半径与直径的夹角(ÐFMG)平分(ÐFMT=ÐTMG),并且一切与切线MT平行的弦被过M点的直径平分(PI=IQ).
如果抛物线的切线的斜率为k,则其切线的方程为
![]()
3° 抛物线的任两切线的夹角等于两切点的焦点半径的夹角的一半.
4° 从焦点F作抛物线在点M的切线的垂线,则垂足的轨迹为在顶点的切线.
4.抛物线各量计算公式
![]()
|
抛物线各量 |
计 算 公 式 |
|
[曲率半径] R
|
式中a为点M(x, y)的切线与主轴的夹角,n为法线MN之长.特别,顶点的曲率半径R0 = p |
|
[弧长]
|
|
|
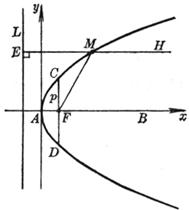
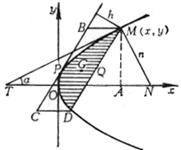
[面积] S |
弓形(MOD)的面积= 即
这里MD弓形弦长,CD平行于主轴,BC与抛物线相切, h为该平行四边形的高(即弓形拱高),特别, |
|
[几何重心] G |
弓形(MOD)的重心 (BC平行于MD,P为切点,PQ平行于Ox) |
五、 一般二次曲线
1.二次曲线的一般性质
上面所列举的椭圆、双曲线、抛物线等,它们的方程关于x,y都是二次的,关于x,y的一般二次方程的形式是
![]()
它所表示的曲线称为一般二次曲线.这里列举它们的一些共同性质.
[直线与二次曲线的交点] 一直线与一个二次曲线交于两点(实的,虚的,重合的).
[二次曲线的直径与中心] 一个二次曲线的平行于已知方向的弦的中点在一直线上,称它为二次曲线的直径,它平分某一组弦.设已知方向的方向数为a,b,则直径的方程为
![]()
或改写为
![]()
由此可见,二次曲线的直径组成一个直线束.束内任一直径通过下列两直线交点:
![]()
1° ![]() 即
即![]() .
.
这时二次曲线的一切直径通过同一点,称为中心,这种曲线称为有心二次曲线,中心的坐标为
![]()
2° ![]() 即
即![]()
(i)
![]() 这时曲线无中心;
这时曲线无中心;
(ii) ![]() 这时曲线有无限个中心,即中心在同一直线上(中心直线).
这时曲线有无限个中心,即中心在同一直线上(中心直线).
这两种曲线称为无心二次曲线.
[二次曲线的主轴(或对称轴)] 如果直径垂直于被它所平分的弦,则称它为二次曲线的主轴(对称轴), 无心二次曲线有一条实的主轴;有心二次曲线有两条实的主轴,它们是互相垂直的,交点就是中心.
[二次曲线的切线与法线]
二次曲线上的一点![]() 的切线方程为
的切线方程为
![]()
在点M与二次曲线的切线垂直的直线称为在点M的法线,它的方程为
![]()
2.二次曲线的不变量
由一般二次曲线的方程
![]() (1)
(1)
的系数所组成的下列三个函数:
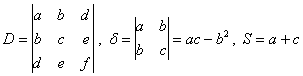
称为二次曲线的不变量,即经过坐标变换后,这些量是不变的.行列式D称为二次方程(1)的判别式.
3.二次曲线的标准方程与形状
|
不 变 量 |
坐标变换后的标准方程 |
曲线形状 |
||
|
有 心 二 次 曲 线 |
|
|
式中 A , C是特征方程 |
|
|
|
有一公共实点的一对虚直线 |
|||
|
|
|
双曲线 |
||
|
|
相交两直线 |
|||
|
|
|
|
||
|
无 心 二 次 曲 线 |
|
式中 |
抛物线 |
|
|
|
|
|
||
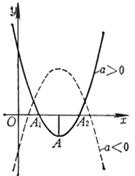
4.二次曲线![]() 的几种情况
的几种情况
|
A |
图 形 |
顶点·中心·焦点参数 |
|
抛物线 |
|
顶点 焦点参数 |
|
椭圆 |
|
顶点 其中 中心 |
|
双曲线 |
|
5.圆锥截线
二次曲线都是用平面切割正圆锥面的截线.因此二次曲线也称为圆锥截线(图7.13)
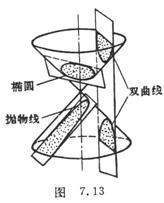 |
用一平面P切割正圆锥时,若P不通过锥顶,且不平行于任一母线,则截线为椭圆;若P不通过锥顶,而平行于一条母线时,截线为抛物线;若P不通过锥顶而平行于两条母线时,截线为双曲线;若P垂直于锥轴,截线为圆.
若P通过锥顶,则椭圆变为一点,双曲线变为一对相交直线,抛物线变为P与圆锥相切的一直线.