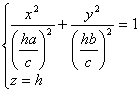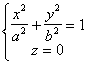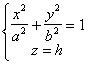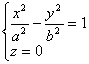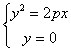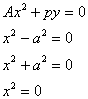§6 二 次 曲 面
一、球面
[球面的方程、球心与半径]
|
方 程 与 图 形 |
球心与半径 |
||
|
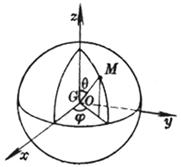
或
(球面坐标方程.式中j为经度,q为余纬度)
|
|
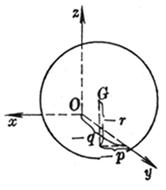
球心 G(0,0,0) 半径 R |
|
|
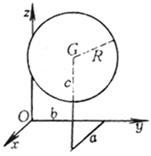
或 (球面坐标方程式中j,q 同上)
|
|
球心 G(a,b,c) 半径 R
|
|
|
方 程 与 图 形 |
球心与半径 |
||
|
|
球心 半径 |
||
[球面的切面与法线] 设一平面P通过球面上一点M且垂直于半径GM,则称P为球面在M的切面.直线MG称为球面在点M的法线.
设球面方程为
![]()
则球面在点M(![]() )的切面方程为
)的切面方程为
![]()
球面在点M(![]() )的法线方程为
)的法线方程为
![]()
[两个球面的交角] 设两个球面
![]() =0
=0
![]() =0
=0
两个球面的交角是指它们在交点的两个切面的夹角,记作q,则
![]()
因公式中不包含交点的坐标,所以在两个球面的交线上的各点的交角必相等.
两个球面的正交条件为
![]()
[球面束·两个球面的根面] 设
![]()
式中![]() 和
和![]() 如(1)式定义,
如(1)式定义,![]() 为参数,则有
为参数,则有
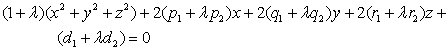
对![]() 的一个确定值,
的一个确定值,![]() 表示一个球面,当
表示一个球面,当![]() 取一切值
取一切值![]() 时,
时,![]() 所表示的球面的全体称为球面束.
所表示的球面的全体称为球面束.![]() 时为一平面,称为两个球面
时为一平面,称为两个球面![]() 的根面,其方程为
的根面,其方程为
![]()
根面与![]() 和
和![]() 的连心线垂直,束中任一球面
的连心线垂直,束中任一球面![]() 的中心在连心线上,且分连心线的比为
的中心在连心线上,且分连心线的比为![]() .
.
[球面汇·三个球面的根轴] 设![]() 和
和![]() 如(1)式定义,又设
如(1)式定义,又设
![]()
设
![]()
式中![]() 为二独立参数,则有
为二独立参数,则有
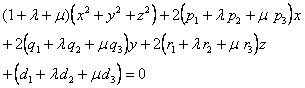
对![]()
![]() 的一对确定值,
的一对确定值,![]() 表示一个球面,当
表示一个球面,当![]() 取一切值
取一切值![]() 时,
时,![]() 所表示的球面的全体称为球面汇.
所表示的球面的全体称为球面汇.
三个球面中每对球面的根面分别为
![]() 和
和![]()
这三个平面交于一条直线,称为![]() 的根轴.
的根轴.
二、椭球面
|
方 程 与 图 形 |
基 本 元 素 |
特 征 |
|
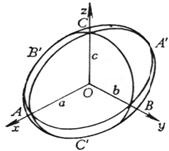
[椭球面]
当a=b时为旋转椭球面 (在Ozx平面上的曲线 当a=b=c时为球面 |
顶点 主轴 主平面及其方程: Oxy平面z=0 Oyz平面x=0 Ozx平面y=0 主轴的方程: AA’ y=z=0 BB’ z=x=0 CC’ x=y=0 中心O(0,0,0) 直径平面 通过中心的平面 |
任一平面与椭球面的交线为一椭圆(特殊情况下为一圆). 平行于一已知方向d的一组弦的中点在一个平面上,该平面是一直径平面,它共轭于方向d. 三个主平面是分别共轭于主轴的直径平面. 椭球体的体积: |
三、双曲面
|
方 程 与 图 形 |
基 本 元 素 |
特 征 |
|
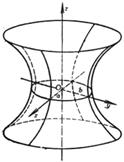
[单叶双曲面]
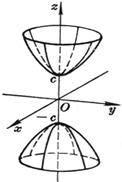
[双叶双曲面] 当a=b时,为 [旋转双曲面] (在Oxz平面上的曲线 绕z轴旋转而得到) |
主轴 中心O(0,0,0) 主平面及其方程: Oxy平面z=0 Oyz平面x=0 Ozx平面y=0 |
平行于z轴的平面与双曲面的交线都是双曲线(对于单叶双曲面,可能是一对相交直线). 平行于Oxy平面的平面与双曲面的交线都是椭圆. 单叶双曲面上有两族直母线,它们的方程是 (l为参数)
与 ( m为参数) |
四、抛物面
|
方 程 与 图 形 |
基 本 元 素 |
特 征 |
|
[椭圆抛物面] 当a=b时,为旋转抛物面 (在Ozx平面上的曲线 [双曲抛物面]
|
顶点O(0,0,0) 主轴 z轴 主平面及其方程: Oyz平面x=0 Ozx平面y=0 |
椭圆抛物面与平行于z轴的平面的交线是抛物线;与平行于Oxy的平面的交线都是椭圆. 体积
体积
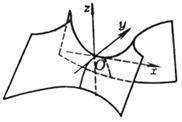
双曲抛物面与平行于Oyz的平面(或平行于Ozx的平面)的交线是抛物线;与平行于Oxy的平面的交线是双曲线. 双曲抛物面的形状呈马鞍形,所以也称为马鞍面. 双曲抛物面上有两族直母线,它们的方程是 与 |
五、 锥面与柱面
|
方 程 与 图 形 |
基 本 元 素 |
特 征 |
|
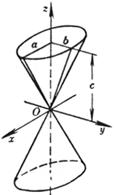
[椭圆锥面] 当a=b时, 为圆锥面 (在Oxz平面上的直线 |
主轴 z轴 顶点 原点O a,b为z=c的平面与锥面的交线(椭圆)的半轴
|
椭圆锥面与平行于Oxy的平面z=h的交线是椭圆 与Oxy平面交于原点O.
|
|
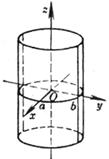
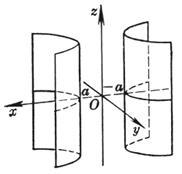
[椭圆柱面] 当a=b时,为圆柱面 |
准线的方程为 母线的方向数为(0,0,1) |
椭圆柱面与任何平行于Oxy的平面的交线都是同样的椭圆 |
|
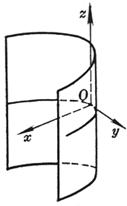
[双曲柱面]
|
准线的方程为 母线的方向数为 (0,0,1)
|
|
|
方 程 与 图 形 |
基 本 元 素 |
特 征 |
|
[抛物柱面] |
准线的方程为 母线的方向数为 (0,0,1) |
|
|
[渐近锥面] 二次锥面 为双曲面 的渐近锥面 |
|
与双曲线的渐近线类似,通过z轴的每个平面与双曲面的交线为一对共轭双曲线,与锥面的交线是两条直线,即这对双曲线的渐近线. |
六、 一般二次曲面
1. 二次曲面的一般性质
上面所列举的椭球面、双曲面、抛物面等,它们的方程关于x,y,z都是二次的.关于x,y,z的一般二次方程的形式是
![]()
它表示的曲面称为一般二次曲面.这里列举这些曲面的一些共同性质.
[直线与二次曲面的交点] 一直线与一个二次曲面交于两点(实的,虚的,重合的).或者这直线全在曲面上,此时称它为二次曲面的直母线或母线.
[平面与二次曲面的交线] 任一平面与一个二次曲面的交线为一个二次曲线.
[二次曲面的直径平面与中心] 一个二次曲面的平行于已知方向的弦的中点在一个平面上,称为直径平面,它平分某一组平行弦.设已知方向的方向数为l,m,n,则直径平面的方程为
![]()
或改写为
![]()
当l,m,n变动时,这个方程表示一个平面把,由此二次曲面的直径平面组成一个平面把.把内任一平面都通过下列三个平面的交点:
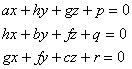
如果交点不在曲面上,则称它为二次曲面的中心,如果交点在曲面上,则称它为二次曲面的顶点.凡有中心的二次曲面称为有心二次曲面,其余的都称为无心二次曲面.
[二次曲面的主平面与主轴] 如果直径平面垂直于被它所平分的弦,则称为主平面(对称平面),每个二次曲面至少有一个实主平面,非旋转二次曲面的任两主平面是互相垂直的,它们的交线为主轴.
[二次曲面的切面与法线] 二次曲面在一点M(![]() )的切面方程为
)的切面方程为
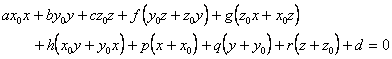
在点M与二次曲面的切面垂直的直线称为曲面在点M的法线,它的方程可写为
![]()
[二次曲面的圆截面] 如果一个平面与一个二次曲面的交线为一个圆,则称该平面为曲面的圆截面.
如果二次曲面不是球面,则通过空间中一点,二次曲面有六个圆截面;其中一般有两个实圆截面,四个虚圆截面;而且六个圆截面中有几个是重合的.
2.二次曲面的不变量
由二次曲面的一般方程
![]() (1)
(1)
的系数组成的下列四个函数:
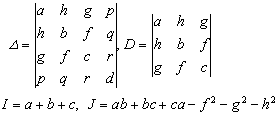
称为二次曲面的不变量,即经过坐标变换后,这些量是不变的.行列式![]() 称为二次方程(1)的判别式.
称为二次方程(1)的判别式.
3.二次曲面的标准方程及形状
|
不 变 量 |
坐标变换后的方程 |
曲 线 形 状 |
||
|
有心二次曲 面 |
D>0 |
式中A,B,C,为特征方程
的三个特征根 |
A,B,C,异号时为单叶双曲面 A,B,C,同号时无轨迹 |
|
|
D<0 |
A,B,C, 同号时为椭球面 A,B,C, 异号时为双叶双曲面 |
|||
|
D=0 |
A,B,C,同号时无轨迹 A,B,C,异号时为二次锥面 |
|||
|
D = 0 无心二次曲 面 |
D<0 |
|
椭圆抛物面 (A,B都是正的时,根号前取负号; A,B都是负的时,根号前取正号) |
|
|
D>0 |
双曲抛物面 |
|||
|
D=0 |
|
|
A,B同号时无轨迹 |
|
|
J = 0 |
|
抛物柱面 一对平行平面 无轨迹 一对重合平面 |
||
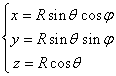
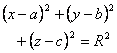
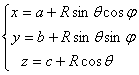
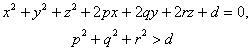
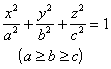

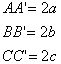
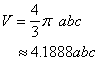

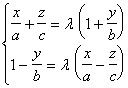
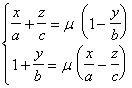

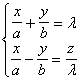 (
( (
(