二、多变量函数的微分

[偏导数及其几何意义]  设二元函数

u=f(x,y)

当变量x有一个改变量Δx而变量y保持不变时,得到一个改变量

Δu=f(x+Δx,y)－f(x,y)

如果当Δx→0时,极限

=

存在,那末这个极限称为函数u=f(x,y)关于变量x的偏导数,记作或,也记作或,即

=====

类似地,可以定义二元函数u=f(x,y)关于变量y的偏导数为

=====

偏导数可以按照单变量函数的微分法则求出,只须对所论变量求导数,其余变量都看作常数.

偏导数的几何意义如下:

二元函数u=f(x,y)表示一曲面,通过曲面上一点M(x,y,u)作一平行于Oxu平面的平面,与曲面有一条交线,就是这条曲线在该点的切线与x轴正向夹角的正切,即=.同样,有= (图5.5).

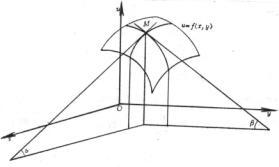
图5.5

偏导数的定义不难推广到多变量函数u=f(x1,x2,…,xn)的情形.

[偏微分]  多变量函数u=f(x1,x2,…,xn)对其中一个变量(例如x1 )的偏微分为

也可记作.

[可微函数与全微分]  若函数u=f(x,y)的全改变量可写为

=+

式中A,B与Δx,Δy无关,,则称函数u=f(x,y)在点(x,y)可微分(或可微),这时函数u=f(x,y)的偏导数,一定存在,而且

=A, =B

改变量Δu的线性主部

=+dy

称为函数u=f(x,y)的全微分,记作

du=+dy                                    (1)

函数在一点可微的充分条件:如果在点(x,y)函数u=f(x,y)的偏导数存在而且连续,那末函数在该点是可微的.

公式(1)具有一阶微分的不变性,即当自变量x,y又是另外两个自变量t,s的函数时,上面的公式仍然成立.

上述结果不难推广到多变量函数u=f(x1,x2,…,xn)的情形.

注意,在一个已知点,偏导数的存在一般说来还不能确定微分的存在.

[复合函数的微分法与全导数]

(1)� 设u=f(x,y),x=(t,s),y=(t,s),则

=+

=+

(2)� 设u=f(x1,x2,…,xn),而x1,x2,…,xn又都是t1,t2,…,tm的函数,则

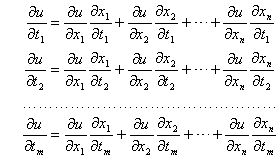
(3)� 设u=f(x,y,z),而y=(x,t),z=(x,t),则

=

 

=

(4)� 设u=f(x1,x2,…,xn), x1= x1(t), x2= x2(t), ,则函数u=f(x1,x2,)的全导数为

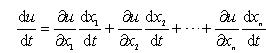
[齐次函数与欧拉公式]  如果函数f(x,y,z)恒等地满足下列关系式 

f(tx,ty,tz)=f(x,y,z)

则称f(x,y,z)是一个k次的齐次函数.对于这种函数,只要它可微,就有

   (欧拉公式)

注意,齐次函数的次数k可以是任意实数,例如,函数

就是自变量x及y的π次齐次函数.

[隐函数的微分法]  设F(x1,x2,…,xn,u)=0,则

………………………

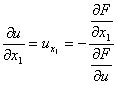
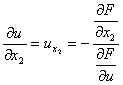
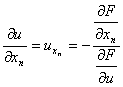
(参考本节,四).

[高阶偏导数与混合偏导数]  函数u=f(x1,x2,…,xn)的二阶偏导数为,,…,和,,,…,后者称为混合偏导数.三阶偏导数为,,…, ,,,…。类似地可定义更高阶的偏导数.

关于函数乘积的混合偏导数有下面公式:设u,都是x1,x2,…,xn的函数,则

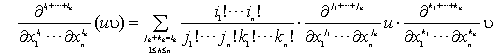
注意,混合偏导数一般与求导的次序有关,但是,如果两个同阶的偏导数,只是求导的次序不同,那末只要这两个偏导数都连续,它们就一定彼此相等.例如,如果在某一点(x,y)函数与都连续,那末一定有

(x,y)= (x,y)

[高阶全微分]  二元函数u=f(x,y)的二阶全微分为

d2u=d(du)=

或简记作

d2u=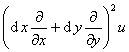

式中偏导数符号,经平方后出现,,,它们再作用到函数u=f(x,y)上,以下类同.

二元函数u=f(x,y)的n阶全微分为

dnu=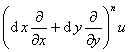

多变量函数u=f(x1,x2,…,xm)的n阶全微分为

dnu=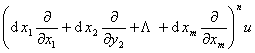

[偏导数的差分形式]

(表中h为x轴方向步长,l为y轴方向步长)

图  示

差 分 公 式

       

   

     

       

 

 

    

   

  

    

   

 

     图  示

差 分 公 式