四、 齐次线性微分方程的幂级数解法
[具有幂级数形式的解] 一般变系数的齐次线性微分方程,不一定能找到用初等函数表示的解,这时可以考虑求具有幂级数形式的解.
现以二阶齐次线性微分方程为例说明解法(高阶方程同样适用).设
![]()
![]()
其中![]() 和
和![]() 在
在![]() 可展成幂级数.要求方程在
可展成幂级数.要求方程在![]() 附近的解,只要先假定这个解具有幂级数形式
附近的解,只要先假定这个解具有幂级数形式
![]()
然后形式地算出所需的各阶导数,代入原方程变成恒等式,确定待定的系数![]() 从而得出所求的幂级数解.
从而得出所求的幂级数解.
如果![]() ,
,![]() 在
在![]() 不能展成幂级数,比如是x的有理分式,而分母在
不能展成幂级数,比如是x的有理分式,而分母在![]() 等于零,这时可试求具广义幂级数形式
等于零,这时可试求具广义幂级数形式
![]()
的解,其中a和![]() 都是待定常数.
都是待定常数.
[求勒让德方程的解] 方程
![]()
称为勒让德方程,它的解称为勒让德函数.
在x=0附近,方程的系数可以展成幂级数,令
![]()
代入原方程,可以定出两个线性无关解
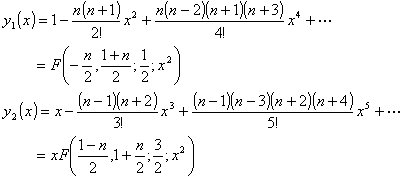
所以勒让德方程的通解为
![]()
式中A,B是任意常数,![]() 是高斯超几何级数.
是高斯超几何级数.
若n为整数,则![]() 与
与![]() 中有一个为多项式,另一个仍然是无穷级数.适当选取任意常数A,B,使当x=1时,多项式的值为1,这个多项式称为勒让德多项式,记作
中有一个为多项式,另一个仍然是无穷级数.适当选取任意常数A,B,使当x=1时,多项式的值为1,这个多项式称为勒让德多项式,记作![]() ,它属于第一类勒让德函数.另一个则与
,它属于第一类勒让德函数.另一个则与![]() 线性无关,它是无穷级数,记作
线性无关,它是无穷级数,记作![]() ,属于第二类勒让德函数.此时,勒让德方程的通解为
,属于第二类勒让德函数.此时,勒让德方程的通解为
![]()
式中A,B为任意常数.
[求贝塞耳方程的解] 方程
![]()
称为v阶贝塞耳方程,式中v为任意实数(或复数),它的解称为贝塞耳函数.
因方程系数![]() ,在x=0不能展成幂级数,而是x的有理分式.令
,在x=0不能展成幂级数,而是x的有理分式.令
![]()
代入原方程,令 x各次幂的系数等于零,得![]() ,先取
,先取![]() =v,得
=v,得
![]()
所以
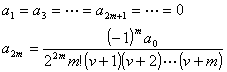
取![]() ,得贝塞耳方程的一个特解,记作
,得贝塞耳方程的一个特解,记作
![]()
它称为v阶第一类贝塞耳函数.
取![]() ,得另一特解
,得另一特解
![]()
当v不为整数时,这两个特解线性无关,此时贝塞耳方程的通解为
![]()
式中A,B是任意常数.
当v=n为整数时,![]() 与
与![]() 线性相关.此时记
线性相关.此时记
![]()
它也是贝塞耳方程的一个解,而且与![]() 线性无关.称
线性无关.称![]() 为n阶第二类贝塞耳函数.于是贝塞耳方程的通解为
为n阶第二类贝塞耳函数.于是贝塞耳方程的通解为
![]()
式中A,B是任意常数.