二、 高阶微分方程的几种可积类型及其解法
1. y(n) = f(x)
将方程写成
![]()
积分后得到
![]()
重复这一过程到积分n次,就得到微分方程的通解:
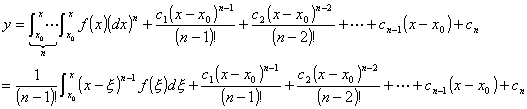
2. F(x,y(n) )=0
1° 若能解出y(n),则方程化成类型1求解.
2° 若不能解出y(n),或解出后表达式太复杂,就设法求它的参数形式的解:
设函数(t),(t) (<t<)满足
F((t),(t))≡0
则原方程可写成参数形式
x=(t), y(n)=(t)
由 dy(n-1)= y(n)dx=(t)'(t)dt
得
![]()
又由 dy(n-2)=y(n-1)dx=1(t,c1)'(t)dt
得
![]()
最后得原方程的参数形式的通解
![]()
3. F(y(n-1), y(n) )=0
1° 若从方程可解出y(n):
y(n)=f(y(n-1))
则令y(n-1)=z,上式化成
![]()
这是变量可分离的方程,设解为
z=(x,c1)
那末化成类型1
y(n-1)=(x,c1)
其通解为
![]()
2° 若不能解出y(n),但原方程可写成参数形式:
y(n-1)=(t), y(n)=(t)
则从 dy(n-1)= y(n)dx
得
![]()
按类型2的方法,可得通解(参数形式)
![]()
4. F(y(n-2), y(n) )=0
设方程可解出y(n):
y(n)=f(y(n-2))
令z=y(n-2),方程两边乘以2z'化成
d(z' 2)=2f(z)dz
积分后有
![]()
用分离变量法求得
z=(x,c1,c2)
那末 y(n-2)=(x,c1,c2)
再积分n-2次就得原方程的通解.