二、格林函数及其物理意义

[格林函数]  在区间[a,b]上，考虑微分方程

Ly+Φ(x)=0

的边值问题，式中L是微分算子：

齐次边界条件为在端点x=a, x=b处，满足，其中α,β为常数。

为了得出这个问题解的形式，首先构造函数G,使对一给定数ξ，

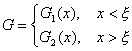
并且满足条件：

(i)  函数G₁和G₂在它们的定义区间上满足LG=0,即当x<ξ时,LG₁=0;当x>ξ时，LG₂=0。

(ii)  函数G满足边界条件，即G₁满足在x=a的边界条件，G₂满足在x=b的边界条件。

(iii)  函数G在x=ξ连续，即G₁(ξ)=G₂(ξ)。

(iv)  G的导数以x=ξ为一不连续点，其跳跃是，即

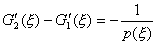
可以证明，若以ξ为参数的这个函数G存在，则原问题的解有如下的形式：

                                                     (2)

例如G(x,ξ)可取

                                                  (3)

式中A是由关系式

决定的一个常数，u(x)是Ly=0满足在x=a处所给定的齐次边值条件的一个解，v(x)是在x=b处满足边值条件的一个解。则G(x,ξ)显然满足条件(i)~(iv)。

此外，还可证明，对由(3)定义的G(x,x),由关系式(2)确定的函数y满足微分方程(1)并且满足u(x)在x=a与v(x)在x=b所规定的相同的齐次边界条件。

满足条件（i）~(iv)或由(3)式所定义的函数称为与微分表达式Ly和边界条件相联系的格林函数。在许多物理问题中，这个函数具有简单的物理意义，将在下一段中说明。

[线性积分方程的一个典型实例]  考虑一条长为l的有弹性的弦，假定在平衡位置时，弦的位置在Ox轴的线段Ol上。在点x施加单位力，于是弦的每一点得到一个离差，在点x处所产生的离差以G(x,x)表示（图15.1）。函数G(x,x)为两点（x和x）函数，在点x施加外力，在点x计量离差，称G为影响函数。

如果弦的两端固定在x轴上A,B两点，弦的张力为T₀,则在点x外处施加的单位力作用下，弦成图15.1所示的形状。根据虎克（Hooke）定律与力的平衡条件，在点x处有

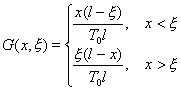
这就是弦的影响函数。

从能量守恒定律可导出G(x,x)的互易原理：在点x处施加外力在点x处产生的离差等于在点x处施加大小相同的力在点x处产生的离差，即

G(x,x )=G(x , x)

如果在弦上施加的力F是连续分布的，并设线性强度是p(x ),则作用于弦上点x 和x +Dx 之间的一小弦段的力就接近于p(x )Dx 。把引起弦变形的这些力元素相加，便得弦的形状

1°  设在某个力的作用下，弦成已知形状y=y(x),求定力分布强度p(x ),就得到含未知函数p(x )的第一类Fr积分方程

                                                      (1)

2°  设作用力随时间t改变，且在点x的强度是

        p(x )sinw t                   (w >0)

则弦的运动是由方程

                             y=y(x)sinw t

描写的周期运动。

设r (x )为弦在点x的线性密度，则在时刻t,点x 与x +Dx 之间的小弦段除受力p(x)sinw tDx 的作用外，还受惯性力

                     sinw tDx

的作用，则等式(1)可化为如下的形式：

                                     (2)

式中

                       

K(x,x )=G(x,x )r (x ),           l =w ²

如果函数p(x)给定，那么F(x)也就给定，这样积分方程(2)就是确定函数y(x)的Fr方程。注意，由于F(x)的定义，有

F(0)=F(l)=0

若密度r (x)=r 是常数，而F(x)有二阶的连续导数，则方程(2)的解为

即

              (3)

式中

把(3)式微分两次就得到

另一方面，可以证明这个微分方程的任一在x=0及x=l处等于0的解是积分方程(2)的解。