四、光学
【光学】 物理学的一个部门。光学的任务是研究光的本性,光的辐射、传播和接收的规律;光和其他物质的相互作用(如物质对光的吸收、散射、光的机械作用和光的热、电、化学、生理效应等)以及光学在科学技术等方面的应用。17世纪末,牛顿倡立“光的微粒说”。当时,他用微粒说解释观察到的许多光学现象,如光的直线性传播,反射与折射等,后经证明微粒说并不正确。1678年惠更斯创建了“光的波动说”。波动说历时一世纪以上,都不被人们所重视,完全是人们受了牛顿在学术上威望的影响所致。当时的波动说,只知道光线会在遇到棱角之处发生弯曲,衍射作用的发现尚在其后。1801年杨格就光的另一现象(干涉)作实验(详见词条:杨氏干涉实验)。他让光源S的光照亮一个狭长的缝隙S1,这个狭缝就可以看成是一条细长的光源,从这个光源射出的光线再通过一双狭缝以后,就在双缝后面的屏幕上形成一连串明暗交替的光带,他解释说光线通过双缝以后,在每个缝上形成一新的光源。由这两个新光源发出的光波在抵达屏幕时,若二光波波动的位相相同时,则互相叠加而出现增强的明线光带,若位相相反,则相互抵消表现为暗带。杨格的实验说明了惠更斯的波动说,也确定了惠更斯的波动说。同样地,19世纪有关光线绕射现象之发现,又支持了波动说的真实性。绕射现象只能借波动说来作满意的说明,而不可能用微粒说解释。20世纪初,又发现光线在投到某些金属表面时,会使金属表面释放电子,这种现象称为“光电效应”。并发现光电子的发射率,与照射到金属表面的光线强度成正比。但是如果用不同波长的光照射金属表面时,照射光的波长增加到一定限度时,既使照射光的强度再强也无法从金属表面释放出电子。这是无法用波动说解释的,因为根据波动说,在光波的照射下,金属中的电子随着光波而振荡,电子振荡的振幅也随着光波振幅的增强而加大,或者说振荡电子的能量与光波的振幅成正比。光越强振幅也越大,只要有足够强的光,就可以使电子的振幅加大到足以摆脱金属原子的束缚而释放出来,因此光电子的释放不应与光的波长有关。但实验结果却违反这种波动说的解释。爱因斯坦通过光电效应建立了他的光子学说,他认为光波的能量应该是“量子化”的。辐射能量是由许许多多分立能量元组成,这种能量元称之为“光子”。光子的能量决定于方程
E=hν
式中E=光子的能量,单位焦耳
h=普朗光常数,等于6.624×10-34焦耳·秒
ν=频率。即每秒振动数。ν=c/λ,c为光线的速度,λ为光的波长。现代的观念,则认为光具有微粒与波动的双重性格,这就是“量子力学”的基础。在研究和应用光的知识时,常把它分为“几何光学”和“物理光学”两部分。适应不同的研究对象和实际需要,还建立了不同的分支。如光谱学,发光学、光度学,分子光学、晶体光学,大气光学、生理光学和主要研究光学仪器设计和光学技术的应用光学等等。
【光】 严格地说,光是人类眼睛所能观察到的一种辐射。由实验证明光就是电磁辐射,这部分电磁波的波长范围约在红光的0.77微米到紫光的0.39微米之间。波长在0.77微米以上到1000微米左右的电磁波称为“红外线”。在0.39微米以下到0.04微米左右的称“紫外线”。红外线和紫外线不能引起视觉,但可以用光学仪器或摄影方法去量度和探测这种发光物体的存在。所以在光学中光的概念也可以延伸到红外线和紫外线领域,甚至X射线均被认为是光,而可见光的光谱只是电磁光谱中的一部分。
【光源】 物理学上指能发出一定波长范围的电磁波(包括可见光与紫外线、红外线和X光线等不可见光)的物体。通常指能发出可见光的发光体。凡物体自身能发光者,称做光源,又称发光体,如太阳、恒星、灯以及燃烧着的物质等都是。但像月亮表面、桌面等依靠它们反射外来光才能使人们看到它们,这样的反射物体不能称为光源。在我们的日常生活中离不开可见光的光源,可见光以及不可见光的光源还被广泛地应用到工农业,医学和国防现代化等方面。光源主要可分为:热辐射光源,例如太阳、白炽灯、炭精灯等;气体放电光源,例如,水银灯、荧光灯等。激光器是一种新型光源,具有发射方向集中、亮度高,相干性优越和单色性好的特点。
【几何光学】 光学中以光的直线传播性质及光的反射和折射规律为基础的学科。它研究一般光学仪器(如透镜、棱镜,显微镜、望远镜、照相机)的成像与消除像差的问题,以及专用光学仪器(如摄谱仪、测距仪等)的设计原理。严格说来,光的传播是一种波动现象,因而只有在仪器的尺度远大于所用的光的波长时,光的直线传播的概念才足够精确。由于几何光学在处理成像问题上比较简单而在大多数情况下足够精确,所以它是设计光学仪器的基础。
【物理光学】 光学中研究光的本性以及光在媒质中传播时各种性质的学科。物理光学过去也称“波动光学”,从光是一种波动出发,能说明光的干涉、衍射和偏振等现象。而在赫兹用实验证实了麦克斯韦关于光是电磁波的假说以后,物理光学也能在这个基础上解释光在传播过程中与物质发生相互作用时的部分现象,如吸收,散射和色散等,而且获得一定成功。但光的电磁理论不能解释光和物质相互作用的另一些现象,如光电效应、康普顿效应及各种原子和分子发射的特征光谱的规律等;在这些现象中,光表现出它的粒子性。本世纪以来,这方面的研究形成了物理光学的另一部门“量子光学”。
【光线】 光源发出之光,通过均匀的介质时,恒依直线进行,叫做光的直进。此依直线前进之光,代表其前进方向的直线,称之为“光线”。光线在几何光学作图中起着重要作用。在光的直线传播,反射与折射以及研究透镜成像中,都是必不可少且要反复用到的基本手段。应注意的是,光线不是实际存在的实物,而是在研究光的行进过程中细窄光束的抽象。正像我们在研究物体运动时,用质点作为物体的抽像类似。
【日蚀】 指地球进入月球的本影中,太阳被遮蔽的情形。当太阳、月球和地球在同一条直线上时便会发生。月球每月都会处于太阳与地球之间,不过日食并不能每月看到,这是因为白道(月球的轨道)平面对地球轨道有5°的倾角。月球可能时而在黄道之上或时而在黄道之下,故其阴影不能落在地球上。只有当太阳、月球和地球在一直线内,才能产生日蚀。如果地球的某一部分在月影之内,即发生日蚀;日蚀有全蚀、偏蚀、环蚀三种。地球上的某些地方正位于月球的影锥之内(即在基本影之内)这些地方就能观看到日全蚀。锥外虚影所射到的地方(即半影内的地方)则看到偏蚀。月球离地球较远的时候,影锥尖端达不到地面,这时从圆锥的延长线中央部分看太阳的边缘,还有狭窄的光环,这就是发生的环蚀现象。环蚀在亚洲,一百年中只能遇见十几次,在一个小地区欲见环蚀者,数百年也难得有一次机会。月影投到地面上,急速向西走,所以某一地点能够看见的全蚀时间非常的短,最长不过七分半钟,平均约3分。日全蚀带的宽度,平均约160公里。在某一地点能够看见日全蚀的机会,非常的少;平均360年只有一次。日全蚀的机会虽少,而需要观测和研究的问题甚多。例如日月相切时刻的测定。爱因斯坦引力说的证明等等。
【木星】 在我国古代称之为岁星,是九大行星中最大也最重的行星,它的直径比地球的直径大11倍,它的质量也比地球重317倍。它的自转周期为9.842小时,是所有行星中最快的一个。木星上的大气分布很广阔,其组成含氢(H2)氮(N2)、沼气(甲烷CH4)及氨气(NH3),因此,其表面完全为昏暗所笼罩着。木星离地球的距离为628 220 000公里,它的赤道直径为142 804公里,比地球要大11倍。虽然它是太阳系最大的一颗行星,但它却有最短的自转周期,比起地球的一天短了14小时6分钟;故知它是以极其惊人的速度不停地自转着,就是在其赤道上的某一质点最少也以时速45 000公里的速度卷旋前进着。离心力在赤道地带也大得惊人,结果便造成赤道的凸出,使此行星变成如一个压扁的橙子一样。木星有四颗大卫星,被命名为木卫一、木卫二…,都能用小望远镜看到,甚至有人能用肉眼观察到。显然它们的体积必定相当可观,它们的直径木卫一约是3719公里,木卫二约是3139公里,木卫三约是5007公里,木卫四约是5184公里。在这四颗卫星中,最靠近木星表面的一颗就是木卫一。由于巨大的卫星引力。木卫一只能以42小时半的时间环绕木星一周。在这些木卫环绕木星的过程中,它们有时在木星之后所谓被掩,有时在木星的阴暗面,称为蚀,有时在木星前叫作凌犯。
【月蚀】 当地球位于太阳和月球之间而且是满月时,进入地影的月球,就会发生月蚀。月球全部走到地影中的时候,叫做全蚀;只有一部分进入本影的时候,叫做偏蚀。月全蚀的时候可分做五象,当月球和本影第一次外切的时候,叫做初亏;第一次内切的时候叫做蚀既;月心和本影中心距离最近的时候,叫做蚀甚;当月球和本影第二次内切的时候,叫做生光;第二次外切的时候叫做复圆。偏蚀时,只有初亏、蚀甚、复圆三种现象。月蚀现象一定发生于望(阴历十五)的时候;但是望的时候,未必发生月蚀。这是因为白道(月球运行轨道)和黄道(地球运行的轨道)不相一致的缘故。但望时的月球如果距离交点太远,将不能发生月蚀;必须在某一定距离之内,才可以发生月食,这一定的界限,叫做月蚀限;这限界是随日、月、地球的距离和白道交角的变化而略有变动,最大值为12.2°,最小值为9.5°。月蚀最长时共维持3小时40分,其中1时40分为全蚀,其余两小时为偏蚀。月蚀如在地平以上发生,则因地球自转,故可见地区超过半个地球。月全蚀时因地球大气反射红光进入地影,故可见古铜色微光之月面。月蚀次数虽较少,但见蚀带极广,而日蚀带狭窄,故同一地区之居民,看见月蚀之次数较日蚀多。
【光速】 一般指光在真空中的传播速度。真空中的光速是物理学的常数之一,它的特征是:(1)一切电磁辐射在真空中传播的速率相同,且与辐射的频率无关;(2)无论在真空中还是在其他物质媒质中,无论用什么方法也不能使一个信号以大于光速c的速率传播;(3)真空中光速与用以进行观测的参照系无关。如果在一伽利略参照系中观察到某一光信号的速率为c=2.99793×1010厘米/秒,那么,在相对此参照系以速度v平行于光信号运动的另一个伽利略参照系中,所观测到的光信号一定也是c,而不是c+v(或c-v),这就是相对论的基础;(4)电磁学理论中的麦克斯韦方程和罗伦兹方程中都含有光速。当用高斯单位来写出这两个方程时,这一点特别明显。光在真空中的速度为c,在其他媒质中,光的速度均小于c,且随媒质的性质和光波的波长而不同。
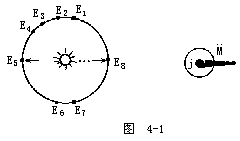
【光速之测定】 伽利略曾经建议,使光行一段7.5千米的路程以测定其速度,但因所用的设备不完善而未成功。此后,直到1675年,丹麦学者罗默在巴黎求得光速之可用数值。罗默把他的观察扩展到宇宙之间,而其所用的研究对象则为木星卫星的成蚀。这些卫星之中最内层的
![]()
因此,每经过此一周期之间隔,M便再次进入木星J之阴影中,而使地球上的观察者暂时无法看到它。罗默发现,当地球E环绕太阳S作公转
![]()
木星卫星的成蚀要迟14秒钟会才发生;又当地球在同一时间(即
![]()
至于木星卫星的实际绕转周期,则可根据地球公转到E5或E8时所作之观测求得。罗默认为此一现象,确实是由于地球从E1运行到W2之时,光之进行必须跟在地球后面追赶上去,而当地球由E6运行到E7时,则光之进行可对着地球迎着赶上所致。由此可知,E1与E2或E6与E7之间的距离,与地球在木星的卫星绕木星一周所需要的时间内运行的路程相符合。因为地球公转速度为30千米/秒,所以此二距离都是等于42.5×60×60×30(千米),约为,4 600 000千米。这说明光需要多走14秒钟始能赶上地球由E1至E2的这一段距离;另一方面它在地球由E6至E7向光迎头赶上的这段距离中,光之行进却能省下14秒钟。由此得到光速约稍大于300 000千米/秒(4 600 000/14≈328 000千米/秒)。当地球由E2远离木星而继续运转至E3、E4…等处时,那么当靠近E5时,则每次成蚀延迟之时间相继地累积起来,直到地球渐近于E5时成蚀延迟时间逐渐减少为零了(此乃由于木星与地球间的距离之增加,由于接近E5而渐渐减少,终于抵达E5而趋于零所致)。故成蚀延迟之时间,当地球在半年之中由E8运转至E5时,每次成蚀延迟时间相加起约等于1000秒。这也就是光从木星到达E5和光从木星到达E8这两段行程所需的时间差(亦即光行经地球公转轨道直径E5E8所需之时间)。由天文学上可知地球公转的轨道这直径为d=300 000 000千米;利用此数值计算出的光速为
![]()
这一数值要比根据每连续两次木星卫星成蚀之时差所求得的光速更可靠一些。罗默测出的光速c=315 000千米/秒,和现在科学家采用更较精细的量度方法在真空中求得之光速的数值c=299 696±4千米/秒,实极接近。c=299 796这个数值是美国物理学家迈克耳孙测出的。在激光得以广泛应用以后,开始利用激光测量光速。其方法是测出激光的频率和波长,应用
c=λν
计算出光速c,目前这种方法测出的光速是最精确的。根据1975年第15届国际计量大会决议,把真空中光速值定为
c=299 792 458米/秒。
在通常应用多取c=3×108米/秒。
【迈克耳孙】 Michelson(1852~1931年)美国物理学家。他创造的迈克耳孙干涉仪对光学和近代物理学是一巨大的贡献。它不但可用来测定微小长度、折射率和光波波长等,也是现代光学仪器如付立叶光谱仪等仪器的重要组成部分。他与美国化学家莫雷(1838~1923年)在1887年利用这种干涉仪,作了著名的“迈克耳孙—莫雷实验,这一实验结果否定了以太的存在,从而奠定了相对论的实验基础。1926年用多面旋镜法比较精密地测定了光的速度。
【光的直线传播定律】 光在均匀媒质中是沿着直线传播的。因此,在点光源(即其线度和它到物体的距离相比很小的光源)的照明下,物体的轮廓和它的影子之间的关系,相当于用直线所做的几何投影。光的直线传播定律是人们从实践中总结出来的。而直线这一概念本身,显然也是由光学的观察而产生的。作为两点间的最短距离是直线这一几何概念,也就是光在均匀媒质中沿着它传播的那条线的概念。所以自古以来,在实验上检查产品的平直程度,均以视线为准。但是,光的直线传播定律并不是在任何情况下都是适用的。如果我们使光通过很小的小孔,则
![]()
我们只能得到一个轮廓有些模糊的小孔的像。孔越小,像越模糊。当孔
![]()
而引起的。
【光的反射】 光遇到物体或遇到不同介质的交界面(如从空气射入水面)时,光的一部分或全部被表面反射回去,这种现象叫做光的反射,由于反射面的平坦程度,有单向反射及漫反射之分。人能够看到物体正是由于物体能把光“反射”到人的眼睛里,没有光照明物体,人也就无法看到它。
【光的反射定律】 在光的反射过程中所遵守的规律:(1)入射光线、反射光线与法线(即通过入射点且垂直于入射面的线)同在一平面内,且入射光线和反射光线在法线的两侧;(2)反射角等于入射角(其中反射角是法线与反射线的夹角。入射角是入射线与法线的夹角)。在同一条件下,如果光沿原来的反射线的逆方向射到界面上,这时的反射线一定沿原来的入射线的反方向射出。这一点谓之为“光的可逆性”。
【漫反射】 当一束平行的入射光线射到粗糙的表面时,因面上凹凸不平,所以入射线虽然互相平行,由于各点的法线方向不一致,造成反射光线向不同的方向无规则地反射,这种反射称之为“漫反射”或“漫射”。这种反射的光称为漫射光。很多物体,如植物、墙壁、衣服等,其表面粗看起来似乎是平滑,但用放大镜仔细观察,就会看到其表面是凹凸不平的,所以本来是平行的太阳光被这些表面反射后,弥漫地射向不同方向。
【平面镜】 镜的反射面是光滑平坦的面,叫做平面镜。普通使用的镜是在磨平后的玻璃背面涂有银,或涂锡和水银的合金。物体放在镜前时,物体即映于镜中而可以看见。这是由于物体反射出的光,于镜面反射后进入眼睛所致。平面镜成像,并非光线实际的集合点,所以叫做虚像。平面镜所成之像的大小和原物体相同,其位置和原物体成对称,因为像和镜面的距离,恒与物体和镜面的距离相等。实物在两平面镜间可引起多次反射而形成复像,其在每镜中除由原物各成一像小,余皆互以他镜之像为物而形成。
【潜望镜】 从海面下伸出海面或从低洼坑道伸出地面,用以窥探海面或地面上活动的装置,其构造与普通的望远镜相同,唯另加两个反射镜使物光经两次反射而折向眼中。潜望镜常用于潜水艇,坑道和坦克内用以观察敌情。
【球面镜】 反射面为球面的镜,可用以成像。球面镜有凹、凸两种,反射面为凹面的称“凹面镜”,反射面为凸面的称“凸面镜”。连接镜面顶点与其球心的直线称为“主轴”。与主轴相近而与它平行的一束光线,被镜面反射后,反射光线(或其延长线)与主轴相交,其交点称为“焦点”。镜面顶点和焦点之间的距离称为“焦距”,等于球半径的一半。凹镜的球心和焦点(实焦点)都在镜前,凸镜的球心和焦点(虚焦点)都在镜后。凹镜有使入射光线会聚的作用,所以也称“会聚镜”,凸镜有使入射光线发散的作用,所以也称“发散镜”。在反射望远镜中用到凹镜;在汽车前面供驾驶员看后面车辆情况的镜子,则是凸镜。
【反射率】 又称“反射本领”。是反射光强度与入射光强度的比值。不同材料的表面具有不同的反射率,其数值多以百分数表示。同一材料对不同波长的光可有不同的反射率,这个现象称为“选择反射”。所以,凡列举一材料的反射率均应注明其波长。例如玻璃对可见光的反射率约为4%,锗对波长为4微米红外光的反射率为36%,铝从紫外光到红外光的反射率均可达90%左右,金的选择性很强,在绿光附近的反射率为50%,而在红外光的反射率可达96%以上。此外,反射率还与反射材料周围的介质及光的入射角有关。上面谈及的均是指光在各材料与空气分界面上的反射率,并限于正入射的情况。
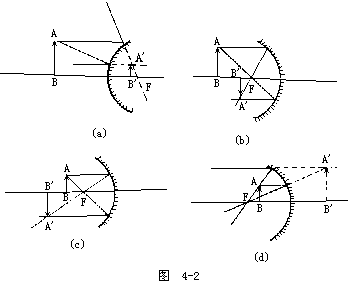
【球面镜成像】 对于凸面镜只能使特成正立、缩小的虚像。如图4-2(a)所示。由物A点出发的平行于光轴的光线,达到镜面后将反射,其反射光的延长线必交球面镜的焦点F上。而从A射向F的光线被球面反射后将平行于光轴。这两条反射线,没有实交点,只有虚交点A′,也就是说视觉认为这两条光线是从A′发出的。物体上的B点发出的沿光轴的光线,即平行于光轴,又过焦点,故B′为B点的像。在物体AB上的各点,接照前述办法作图,其各点的像点都在A′B′上,故A′B′即为AB的像。无论物AB在何处,它所发出的光射到球面镜后而反射的光,没有实交点,因此所成之像必为虚像。由图中可以看出,物体在轴的上方,所成的虚像也在轴的上方,故所成之像为正立。无论AB在什么位置,从A点出发的平行于轴的光线一定在AF方向的光线的上方。此两线的交点A′必比A点更靠近轴,所以像是缩小的。根据上述方法作图可知凹透镜成像可有三种情况:(1)物在凹镜前二倍焦距以外时,是倒立缩小的实像,见图4-2(b)。(2)物在两倍焦距以内,焦点以外时,则成倒立放大的实像,见图4-2(c)。(3)当物位于焦点以内时,则成正立的放大的虚像,见图4-2(c)。
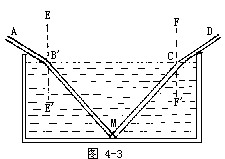
【光的折射】 凡光线在通过疏密不同介质交界面时改变方向的现象,称为光之折射。如图4-3所示,光线AB由空气内斜向射至水面,自入射点B起,就向这点的法线EE′偏折而取BM的方向。若在水底置一平面镜M,使反射线MC再由水中透入空气,则自入射点C起,离开法线FF′偏折,而取CD的方向。偏折后的光线BM和CD,称为折射线,折射线和法线所成的角,如∠E′BM和∠FCD,称为折射角。由此可知光线由稀的介质入射到密的介质时,折射线常向法线偏向,故折射角常比入射角小;若由密的介质透入稀的介质时,折射线常离法线而偏向,折射角常比入射角大。当光线通过介质的密度在不断变化时,光线前进的方向也随之而改变,因此我们隔着火盆上的热空气看对面的东西时,会觉得那东西不停地在闪动着。这是由于火盆上面的空气因受热很快地上升,这部分空气的密度便和周围空气的密度不同,而且热度还不断在变化,当由物体射来的光线通过这样的空气,其折射光线的路径不断发生变化,就会使物体变成了闪动的形状。在炎夏中午时分,假使躺在地上来看树木、房屋和人物,它们的轮廓好像是透过一层流动的水一样,而且动摇不定。这是因为那时十分炎热,地面的辐射热很多,温度高,接近地面的空气受热,密度变小,因而上升,成为向上流动的气流,由物体射来的光线通过这种变动着的气流折射光线的路径就不断改变,因此所看到的物便都动摇不定。我们在夜里看到天空中恒星的闪动,也是这个道理。大气里经常存在着密度不同的气流和旋涡,当恒星的光线通过这种气流时,就会使它原来折射的路径发生变化,一会儿到左,一会儿到右,恒星是不会闪动的,都是这折射光造成的。又如太阳位于地平线附近时,光之折射作用尤大。在地平线下的太阳,阳光从太空(真空)平射至逐渐变化的光密媒质空气中而发生的折射,光线传到地面是一曲线,因为光之折射的关系,太阳看上去就如同刚刚接触到地平线的下缘一样,其实它业已落至地平线以下了。同理,当太阳刚刚还在地平线下的时候,看上去它已升起来了。所以我们可以说:太阳实际上比我们肉眼所见的要落得早些而起的迟些;这等于说,光之折射将我们的白天稍稍加长了一点。
【折射定律】 在光的折射现象中,确定折射光线方向的定律。当光由第一媒质(折射率n1)射入第二媒质(折射率n2)时,在平滑界面上,部分光由第一媒质进入第二媒质后即发生折射。实验指出:(1)折射光线位于入射光线和界面法线所决定的平面内;(2)折射线和入射线分别在法线的两侧;(3)入射角i的正弦和折射角i′的正弦的比值,对折射率一定的两种媒质来说是一个常数,即
![]()
此定律是几何光学的基本实验定律。它适用于均匀的各向同性的媒质。用来控制光路和用来成象的各种光学仪器,其光路结构原理主要是根据光的折射和反射定律。此定律也可根据光的波动概念导出,所以它也可应用于无线电波和声波等的折射现象。
【折射率】 表示在两种(各向同性)媒质中光速比值的物理量。光从第一媒质进入第二媒质时(除垂直入射外),任一入射角的正弦和折射角的正弦之比对于折射率一定的两种媒质是一个常数。这常数称为“第二媒质对第一媒质的相对折射率”。(n12),并等于第一媒质中的
![]()
第一媒质)的折射率称为这媒质的“绝对折射率”,简称“折射率”。由于光在真空中传播的速度最大,故其他媒质的折射率都大于1。同一媒质对不同波长的光,具有不同的折射率;在对可见光为透明的媒质内,折射率常随波长的减小而增大,即红光的折射率最小,紫光的折射率最大。通常所说某物体的折射率数值多少(例如水为1.33,玻璃按成分不同而为1.5~1.9),是指对钠黄光(波长5893×10-10米)而言的。
【光密与光疏媒质】 折射率较大的媒质(光在其中速度较小)与折射率较小的媒质(光在其中速度较大)相比较,前者称“光密媒质”,后者称“光疏媒质”。如水对空气为光密,空气对水为光疏。光从光疏媒质进入光密媒质时,要向接近法线方向折射,即折射角小于入射角;光从光密媒质进入光疏媒质时,要离开法线折射,即折射角大于入射角。
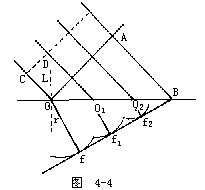
【折射定律的解释】 折射定律的解释,是利用原始形态的惠更斯原理。这种形式的惠更斯原理,实质上是几何光学的原理,并且严格地说,只有在几何光学适用的条件下,也即在光波的波长和波阵面的线度相比为无穷小时,才能够加以应用。在这些条件下,它使我们能够导出几何光学的折射定律。假设以v1表示第一种媒质中的光波速度,以v2表示第二种媒质中的波速。设i是波阵面的法线OC与折射媒质表面的法线OD之间的夹角,见图4-4。设在时刻t=0,波阵面的C点到达媒质表面时,和点O重合,则在波阵面从A′点到达第二种媒质(点B)所需的时间为τ,次波便从作为中心的点O出发,传播到某一个距离Of。以点O1,O2等为中心的各个次波,到指定时刻都传播到相应的距离,在第二种媒质中给出许多元球面波f1、f2……。按照惠更斯原理,诸元波的包络面,即平面Bf2f1f,指出波阵面的实在位置。显然
![]()
将数值A′B=v1τ和Of=v2τ代入式中,得到:
v1τsinr=v2τsini
或
![]()
由此看到,惠更斯的理论解释了折射定律,并且很容易使折射率的数值和傅科在150多年以后所做的实验结果相符。应当注意,在折射现象中,光经过两种媒质,所以折射率与两种媒质有关,当光由媒质Ⅰ射入媒质Ⅱ,这个折射率是指媒质Ⅱ对媒质Ⅰ的相对折射率,通常记作
![]()
折射率,通常用n来表示,显然
![]()
【全反射】 光由光密(即光在其中传播速度较小的)媒质射到光疏(即光在其中传播速度较大的)媒质的界面时,全部被反射回原媒质内的现象。光由光密媒质进入光疏媒质时,要离开法线折射,如图4-5所示。当入射角θ增加到某种情形(图中的e射线)时,折射线延表面进行,即折射角为90°,该入射角θc称为临界角。若入射角大于临界角,则无折射,全部光线均反回光密媒质(如图f、g射线),此现象称为全反射。当光线由光疏媒质射到光密媒质时,因为光线靠近法线而折射,故这时不会发生全反射。
【临界角】 光从光密媒质射到光疏媒质的界面时,折射角大于入射角。当折射角为90°时,折射光线沿媒质界面进行,这时的入射角称为“临界角”。当入射角大于临界角时,折射定律就无法适用了,而只会发生全反射现象。光由水进入空气的临界角约为48.5°,从玻璃进入空气的临界角,随玻璃的成分不同而异,约在30°~42°之间。利用光的折射定律可以求出其临界角。应注意,这时光是由光密媒质射向光疏
![]()
如果光是由某种媒质射向空气界面,则n是该媒质对空气的折射率,
![]()
![]()
![]()
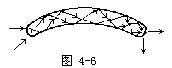
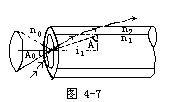
【光导纤维】 光导纤维是利用全反射规律而使光沿着弯曲途径传播的光学元件。它是由非常细的玻璃纤维组成束,每束约有几万根,其中每根通常都是一种带套层的圆柱形透明细丝,直径约为5~10微米,可用玻璃、石英、塑料等材料在高温下控制而成。它已被广泛地应用于光学窥视(传光、传像)和光通讯。光导纤维的结构如图4-6所示,内层材料选取的折射率大,外层材料的折射率低,就是要在内外层之间的界面上产生全反射,以保证光的传输效率。如图4-7所示,单箭头线表示临界光线,它在内外层分界面上的入射角等于或小于临界角A。若在折射率为n0的媒质中入射角大于i0的那些光线(以双箭头表示),在n1、n2分界面上的入射角就小于A,这些光线无法通过纤维而在其中传播。只有在媒质n0中其顶角为2i0的锥体内的全部光线才能在光学纤维中传播,根据临界角的定义。
![]()
和折射定律
n0sini0=n1sini1
可得
![]()
所以对于一定的n1和n2,i0的值是固定的,纤维所容许传播的光线所占的范围是一定的。要使更大范围内的光束能在光学纤维中传播,应该选择n1和n2的差值较大的材料。通常把n0sini0的值叫做光导纤维的数值孔径。光导纤维可用于潜望镜和内窥视系统,它可以窥视人眼所观察不到的或有损于人体健康的地方。国防上可以制成各种坦克、飞机或舰艇上的潜望镜。医学上可以用来制作胃、食道、膀胱等内腔部位进行检查和依断的各种医用窥镜。如果配有大功率激光传输的光学纤维,还可进行内腔激光治疗。由于光纤通讯与电通讯相比具有许多优点,诸如抗电磁干扰性强、频带宽和保密性好、通讯容量大,设备轻巧,制取纤维的二氧化硅的资源又十分丰富。近年来已有数百条光纤通讯线路在世界各地进行试验或正式运动。光导纤维的问世,为光能的应用开辟了更广阔的天地。
【棱镜】 透明材料(如玻璃、水晶等)做成的多面体。在光学仪器中应用很广。棱镜按其性质和用途可分为若干种。例如,在光谱仪器中把复合光分解为光谱的“色散棱镜”,较常用的是等边三棱镜;在潜望镜、双目望远镜等仪器中改变光的进行方向,从而调整其成像位置的称“全反射棱镜”,一般都采用直角棱镜。
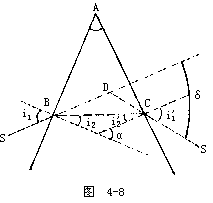
【棱镜的偏向角】 光通过一三棱镜的偏向角等于入射角与出射角之和减去棱镜的折射棱角。如图4-8所示。a为棱镜的折射棱角,当光束SB入射到棱镜时,经连续发生两次折射,出射光线(CS′和入射光线SB之间的夹角,叫做偏向角“δ”。由图不难看出:
δ=(i1-i2)+(i′1-i′2)=(i1+i′1)-(i2+i′2)=i1+i′1-a
如果保持入射线的方向不变,而将棱镜绕垂直于图面的轴线旋转,则偏向角必然随之而改变。可以证明,如果入射角等于出射角时,即在i1=i′1时,则偏向角最小,称为最小偏向角。用δmin表示。
δmin=2i1-α
由此可得
![]()
又当i1=i′2时,折射角
![]()
利用这两个特殊的入射角和折射角,可以计算棱镜材料的折射率
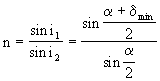
利用最小偏向角测折射率,非常方便也很精确。折射棱角a很小的棱镜,光线通过它时产生的偏向角可按下列方法推出。即由折射定律可知
sini1=nsini2,sinii′1=nsini′2。
在折射棱角a很小和近轴光线的条件下,△BEC的底角i2,i′2很小,所以
i1≈ni2,i′1≈ni′2
则有
δ=ni2+ni′2-α=n(i2+i′2)-α=(n-1)α
运用这个近似关系,可以推导出薄透镜的物像关系式。
【色散】 复色光被分解为单色光,而形成光谱的现象,称之为“色散”。色散可通过棱镜或光栅等作为“色散系统”的仪器来实现。例如,白色光线射于三棱镜,则通过棱镜之后,光线被分散为由不同颜色光组成的色彩光谱。如一细束阳光可被棱镜分为红、橙、黄、绿、蓝、靛、紫七色光。这是由于复色光中的各种色光的折射率不相同。当它们通过棱镜时,传播方向有不同程度的偏折,因而在离开棱镜则便各自分散。折射率较大的紫色光偏向大,而折射率较小的红光则偏向小。由于各色光的折射率有大小之分(这是由于各色光的频率不同造成的,频率高的折射率大),所以非单色光才会发生色散。当一白光由空气射入水或玻璃时,折射后分成各色的光,若玻璃为两面平行的平板,则光从玻璃射出的线平行,不同色光再行重叠,并未发现色散现象。若光通过棱镜,不同色光之出射线不平行,色散现象较易观察。
【光谱】 复色光经过色散系统(如棱镜、光栅)分光后,被色散开的单色光按波长(或频率)大小而依次排列的图案。例如,太阳光经过三棱镜后形成按红、橙、黄、绿、青、蓝、紫次序连续分布的彩色光谱。红色到紫色,相应于波长由7,700~3800×1010米的区域,是为人眼能感觉的可见部分。红端之外为波长更长的红外光,紫端之外则为波长更短的紫外光,都不能为肉眼所觉察,但能用仪器记录。因此,按波长区域不同,光谱可分为红外光谱,可见光谱和紫外光谱;按产生的本质不同,可分为原子光谱、分子光谱;按产生的方式不同,可分为发射光谱、吸收光谱和散射光谱;按光谱表观形态不同,可分为线光谱、带光谱和连续光谱。光谱的研究已成为一门专门的学科,即光谱学。光谱学是研究原子和分子结构的重要学科。
【透镜】 光学仪器的一种重要元件,由透明物质(如玻璃、水晶等)制成。光线通过透镜折射后可以成像。按照其形状或成像要求的不同,透镜可分为许多种类,如两面都磨成球面,或一面是球面另一面是平面的称“球面透镜”;两面都磨成圆柱面,或一面是圆柱面一面是平面的称“柱面透镜”。透镜一般可分为凸透镜和凹透镜两大类。
【凸透镜】 凸透镜是中央部分较厚的透镜。凸透镜分为双凸、平凸和凹凸(或正弯月形)等形式,如图4-9所示。薄凸透镜有会聚作用故又称聚光透镜,较厚的凸透镜则有望远、发散或会聚等作用,这与透镜的厚度有关。将平行光线(如阳光)平行于轴(凸透镜两个球面的球心的连线称为此透镜的主光轴)射入凸透镜,光在透镜的两面经过两次折射后,集中在轴上的一点,此点叫做凸透镜的焦点(记号为F),凸透镜在镜的两侧各有一焦点,如为薄透镜时,此两焦点至透镜中心的距离大致相等。凸透镜之焦距如图4-10所示,是指焦点到透镜中心的距离,通常以f表示。凸透镜球面半径越小,焦距越短,凸透镜可用于放大镜、老花眼及远视的人戴的眼镜、显微镜、望远镜的透镜等。
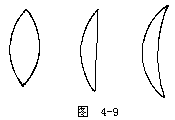
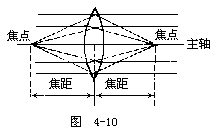
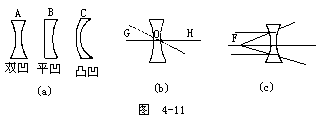
【凹透镜】 两侧面均为球面或一侧是球面另一侧是平面的透明体,中间部分较薄,称为四透镜。分为双凹、平凹及凸凹透镜三种,如图4-11a所示之A、B、C。其两面曲率中心之连线图4-11b所示之G1H,称为主轴,其中央之点O称为光心。通过光心的光线,无论来自何方均不折射。图4-11c表示,平行主轴之光束,照于凹透镜上折射后向四方发散,逆其发散方向的延长线,则均会于与光源同侧之一点F,其折射光线恰如从F点发出,此点称为虚焦点。在透镜两侧各有一个。凹透镜又称为发散透镜。四透镜的焦距,如图4-12所示。是指由焦点到透镜中心的距离。透镜的球面曲率半径越大其焦距越长,如为薄透镜,则其两侧之焦距相等。
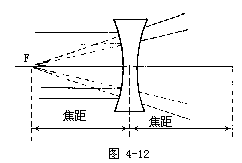
【物和像】 人们能感觉到物,是由于物体各点所反射的光,经过人眼这个光学系统(相当一个焦距可调的凸透镜)成像于视网膜上,再由视神经传到大脑而造成视觉,从光学的角度讲,物点是发散光束的顶点,所以物就是由这些发散光束顶点的组合而成。如果光束经不同媒质的界面反射或折射以后,光线的方向虽然改变了,但反射光线或折射光线所构成的光束仍然有一个顶点“P′”,这个顶点P′就叫做像点,在这种情况下,每个像点和物点间建立了一一对应的关系。这些像点的组合就是像。如果光束中各光线确实在某点会聚,那么该会聚光束的顶点叫做实像;如果光束经界面反射或折射后是发散的,但这些光线反向延长后,能够找到光束的顶点,则该发散发束的顶点叫做虚像。物和像则是这些光束顶点的集合。在空间中的物,它向所有方向反光,眼睛无论在何处,只要找对方向都可以看到物。像则不然,因为平面镜或透镜的反射或折射的光束不是向所有方向,光束总是局限在一定的范围内。如果人眼恰处于光束所在的范围内,便可看到像,但是当眼睛位于反射或折射光束的范围之外时,眼睛是看不到像的。因为这些光束不能进入人的眼睛。
【实像和虚像】 物体发出的光线经过光具组(如反射镜、透镜组等)反射或折射后,重新会聚而造成的与原物相似的图景,实像可以显映在屏幕上,能使照像底片感光。摄影或放映电影都必须利用实像。若物体发出的光线经光具组反射或折射后,如为发散光线,则它们反向的延长线(虚光线)相交时所形成的像称为“虚像”。虚像不能显映在屏幕上,也不能使照像底片感光,只能用人眼观察到。在放大镜、显微镜、望远镜等光学仪器中观察到的像都是虚像。
【虚物】 在光具组中,常按不同的要求使几个透镜来达到成像的目的,以两个透镜为例,如果第一个透镜所形成的实像位于第二个透镜的后面,则对第二个透镜来说,这像就称为“虚物”。
【光学的特定名称】 在研究透镜成象光学中有几个重要的特定名称。它们是:(1)主光轴它是连接透镜两球面曲率中心的直线。(2)副光轴——通过光心的任意直线。所以副光轴有无数条。(3)光心——透镜主轴上的一个特殊点。通过光心的光线,其出射方向和入射方向互相平行,但可有旁向的平行位移,对薄透镜一般认为其方向不变。薄透镜的中心可以近似地当作光心,射向薄透镜中心的光线可认为无折射地通过。(4)焦点——平行光束经透镜折射或曲面镜反射后的交点。有实焦点和虚焦点两类。薄透镜两边的焦点对称。而一般透镜的第一焦点(物方焦点)和第二焦点(像方焦点)不对称。(5)主焦点——平行于透镜的主光轴的平行光束,经反射或折射后和主光轴相交的点。(6)副焦点——平行于跟主光轴夹角不大的副光轴的光线,经透镜折射后会聚(或发散光线的反方向的延长线)于该副光轴上的一点。副焦点都处在焦平面上。(7)焦平面——通过透镜(球面镜)主焦点并和主光轴垂直的平面。和主光轴成任意角度的平行光线经折射后相交的交点,均处于焦平面上。(8)焦距——薄透镜的中心到焦点之间的距离。(9)焦度——透镜或透镜组焦距的倒数。会聚透镜的焦度规定为正,发散透镜的焦度规定为负。如果焦距用米作单位时,焦度的单位叫做屈光度;而眼镜的焦度通常用度作为单位,1度为1屈光度的百分之一。
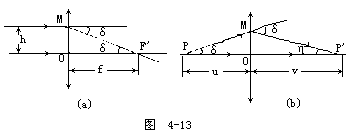
【物像公式】 描述物像位置以及它们和透镜或透镜组的特征量之一(焦距)之间的关系式。对一个薄凸透镜可以认为是由底面朝向透镜中央的许多棱镜的集合,而这些棱镜的顶角是很小的,对于顶角很小的棱镜来说,如果构成棱镜的材料的折射率为n,顶角为A,那么在近轴光线的条件下,其偏向角δ为常数(n-1)A。当棱镜给定后,近轴光线的偏向角δ是不变的。我们可以利用此关系来推导薄透镜的物像公式。如图4-13a所示,设PM为平行光束所任一条光线在M点入射,而OM=h,则出射光线MF′必通过透镜的焦点F′,OF′=f,f为透镜的焦距。根据近轴光线的条件,即f>>h,偏向角近似为
![]()
当主轴的物点P发出的任一近轴光线PM入射到透镜的M点时,图4-13b所示,在理想成像的条件下,出射光线MP′和主轴的交点P′为像点,此时偏向角也应相同。令物距OP=u,像距OP′=v,由图b中的几何关系可知
ξ+η=δ
在近轴光线的条件下,可得
![]()
![]()
![]()
![]()
该式叫做高斯公式。平面镜、球面镜和薄透镜所形成的像的位置,可以根据物像关系式求得,最基本的公式有两个,即高斯公式
![]()
![]()
其中u是物距——代表物到透镜(或面镜)的距离;v是像距——代表像到透镜(或面镜)的距离;f为透镜的焦距。K是像的横向放大率。此二关系式对三种光具组都适用。下表表明在三种透镜中应用情况。
|
光具 公式 |
透镜 |
球面镜 |
平面镜 |
|
焦距 |
|
|
f→∞ |
|
物像公式 |
|
|
|
|
横向放大率 |
|
|
|
【符号法则】 用物像公式进行计算时,应注意关系式中的各项都是代数值。因为只有取代数值,公式才具有普遍意义,否则会造成、凹球面、凸球面、凹透镜、凸透镜的物像公式各不相同,把问题变得复杂。各特定光学量的符号的采用法则是很重要的,若符号选错,则所有的计算全都错了。下面就其应用法则归纳为:(1)所有距离从光心(或顶点)量起;(2)对于实像v取正值,对于虚像v取负值;对于实物u取正值,对于虚物u取负值;(3)凡已知量,其数值前必须冠以符号;凡未知量,必须根据求出的符号来确定物像的性质和位置;(4)会聚透镜(或凹面镜)的焦距为正(实焦点);发散透镜(或凸面镜)的焦距为负(虚焦点)。物像公式,正确运用符号法则,只要知道物体离开透镜(或球面镜)光心的距离u和焦距f,就可以求出成像的位置、像的性质和像的大小。应该注意的是,在球面反射和薄透镜折射时,物像公式只有在近轴光线,近轴物的情况下才适用。因此成像关系式是近似的。
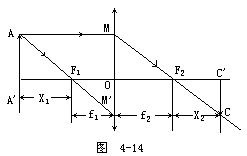
【牛顿公式】 设X1表示物体与第一焦点的距离,而X2表示光像与第二焦点的距离,由图4-14可以看出,△CC′F2~△MOF2和△M′OF1~△AA′F1放大率
![]()
即
X1X2=f1f2
对于薄透镜来讲,f1=f2=f,所以有
X1X2=f2
![]()
著,运用时也较方便。
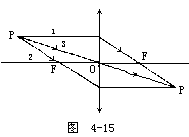
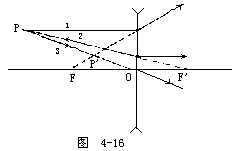
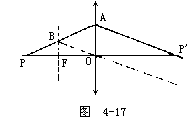
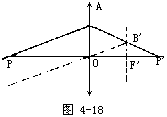
【透镜成像作图】 各种透镜成像作图中,应注意,实际光线用实线画出,在每一条光线上还必须标明箭头,以示光的传播方向。其辅助线,引伸线通常不用实线而采用虚线,以免和实际光线混淆。最后,光线作图法的目的是确定像的位置、性质和大小,因此作图可在方格纸上完成,图中标明比例和所有已知量及待定量的数值。即称为按比例成像作图法。(1)凸透镜成像作图——这一作图主要是三条光线。如图4-15所示。其中PF为通过主焦点的入射线经透镜折射后平行于主轴。而POP′为通过光心的入射线不改变方向。由P点出发平行于主光轴的入射线折射后通过主焦点。此三条线必交于同一点P′,P′便是P点的像。为了简便只要用其中的两条线便可确定像点的位置;(2)凹透镜成像作图的三条光线,如图4-16所示。平行于主轴的入射线,经透镜折射后的出射线的反向延长线通过和物同侧的虚主焦点。由P点射向透镜另一侧虚主焦点的入射线,折射后平行于主光轴。由P点射出通过光心的线不改变方向。其前两条线的反向延长线与第三条线均交于P′点。P′点便是P点的虚像;(3)凸透镜的任意光线作图法。如果物点P在主轴上,则上述的三条光线便合为一条而无法作图,此时像的位置可利用副光轴和焦平面的性质来确定。利用第一焦平面的作图方法,如图4-17所示。经P点作一条入射光线PO,它沿着主轴方向穿过透镜方向不变;经P点作一条任意光线PA,交透镜于A点并与第一焦平面交于B点;作副光轴BO,过A点作和BO平行的线AP′,交主光轴的P′点,P′便是P的像点。同理,也可用第二焦平面作图,其作法如图4-18所示。作任意光线PA交透镜于A点;过透镜中心O作平行于PA的辅助线OB′,与第二焦平面交于B′点;连接A、B′两点且延长,与沿主轴的光线交于P′点,则P′点即为所求也像:(4)凹透镜的任意光线作图法。利用凹透镜的副光轴和焦平面作图,如图4-19所示。经P点作任意光线PA,交透镜于A点,经透镜的中心O作平行于PA的副光轴OB′,和第二焦平面交于B′点;连接A、B′两点,它和延主轴的光线交于P′,则P′点为所求之像点。
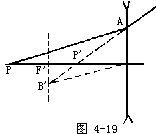
【凸透镜成像规律】 从图4-20可以看出,随着物和焦点之间的相对位置的不同,成像的情况也不同。大致可分为6种情况说明,如图4-20所示。(1)物位于无穷远时,则像距v=f,成实像,放大率K=0。可用于测定焦距;(2)当∞>u>2f时,像的位置f<v<2f,这时是倒立实像,放大率K<1。眼睛、照像机均相当于这种成像关系;(3)当u=2f时,v=2f,这时是倒立实像,放大率K=1,即物像的大小相等;(4)2f>u>f时,2f<v<∞,倒立实像,K>1,放大像。幻灯机,显微镜,均是这种成像关系;(5)u=f时,则v→∞这时无像,这时K→∞放大,探照灯是这种光学关系;(6)f>u>0时,v<O,正立虚像,K>1放大,放大镜是这种光学成像关系。图中的2、3、4、5、6各种情况,分别代表(1)、(2)、(3)、(4)、(5)、(6)所说之情况。
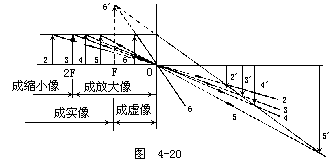
【凹透镜的成像规律】 凹透镜所成的像,无论物体的位置在焦点以外还是焦点以内,它经凹透镜折射后,所成的像,都是缩小的,正立的虚像。像和物在透镜的同侧。因此它的成像规律,不同于凸透镜那样复杂。如图4-21所示。
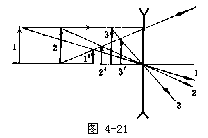
【眼睛】 人的眼睛是一个光学系统。它的构造可以简化为一个单凸透镜和一个屏幕。从物体的两端反射出的两条光线对眼睛的光心点所张的角,叫做视角。物体越小或距离越远,视角越小。观察很小或很远的物体,常使用放大镜、显微镜和望远镜等以增大射角。不是在任何距离处的物体人眼都能看清楚。眼睛能看清物体必要的条件是:(1)物体的像不但要落在视网膜上,并用要落在黄斑中央的中央凹处;(2)像应该有一定的照度。进入眼中的光通量是由瞳孔自行调节,达到一定照度。这一照度是在视网膜透应机能范围之内;(3)视角一般不能小于1′(长1厘米的线段在距眼睛34米处的视角约为1′)。由眼睛的调节作用(或称调焦)所能看得清楚的最远和最近两点,分别叫做远点和近点。正常眼睛远点在无穷远处,近点在10厘米到15厘米处。在适当的照度下,物体离开眼睛25厘米时,在视网膜上造成的像最清晰,并且看起来不易感到疲劳,这个距离叫做明视距离。人的眼睛就是一个透镜系统。外界的景物通过成像在视网膜上而被视觉神经所感受。
【近视眼】远处物体无法成像于视网膜上,而在网膜前,这时要带近视镜。这是由于近视眼的晶状体比正常眼睛凸一些,或视网膜距晶状体的距离过远,所以造成远处的平行光不能会聚在视网膜上,而会聚在视网膜之前,这说明近视眼的远点不在远穷远处。故不能看清远处物体,只能看清一定距离内的物体。为了矫正近视眼,应采用凹透镜制成的眼镜,使光通过眼镜先发散,再通过晶状体会聚,使会聚点后移到视网膜上。
【远视眼】无穷远处的物体所成的像只能在视网膜后面。这是由于视网膜到晶状体的距离过近,或晶状体比正常人眼扁平所致。远视眼的近点比正常人眼远,所以视力范围比正常人眼小。矫正远视眼的方法是用凸透镜做眼镜,使光线在进入眼睛之前,先由凸透镜会聚,以达到使会聚点移前而达到视网膜上。
【眼镜】用以矫正视力或保护眼睛的简单光学器件。由镜片(一般为透镜)和镜架组成。矫正视力的眼镜可分为三种:(1)近视眼镜:由凹透镜制成,能把原先落在视网膜前的像移后到视网膜上;(2)远视眼镜和老光眼镜:由凸透镜制成,能把原先落在视网膜后的像移前到视网膜上;(3)散光眼镜:由球柱面透镜或复曲面透镜制成,以矫正由于角膜各方向曲率不同所引起的像散。保护眼睛用的眼镜有防护镜、防风镜和太阳镜等,用以保护眼睛免受灼伤、暴风袭击、强烈紫达线辐射和红外线的刺激,以及防止强光刺激等。
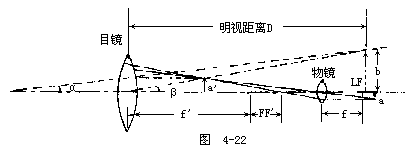
【显微镜】显微镜为一使微小物构成放大虚像的透镜系统。最简单之显微镜为单显微镜,系一收敛透镜,俗称放大镜。通常我们所说的显微镜是指复显微镜的简称,用以观察极微小的物体。显微镜是1610年伽利略发明的。其最简单的型式只包括两个凸透镜,用一个直立金属圆筒,上下两端各装一个焦距极短的物镜和一个焦距较长的目镜,为了消除像差,实际上二透镜均已各由数个透镜组合所取代。图4-22是以基本的单片透镜构造说明显微镜的工作原理。物体置于物镜焦点稍外,得到倒立放大实像于目镜的焦点稍内处;再经目镜折射产生放大虚像于明视距离处。显微镜的放大率为m,在明视距离D处的虚像对眼睛所张的视角为β,并设物体置于D距离处,直接看物的视角为α,则β与α之比值等于显微镜的放大率即m=β/α。求得虚像与物体的大小之比,则可求得显
![]()
![]()
显微镜的放大率是目镜与物镜放大率的乘积
![]()
因物镜的放大率,通常为5~40倍,目镜约为3~20倍,所以一般显微镜的放大率最大约为800倍。如果选用放大倍数更大的物镜时,必须在物体与物镜之间,充以折射率与透镜接近的油,这种镜头叫做油浸镜头,利用油浸镜头可使放大倍数达2000倍。最近又发明一种激光断层共轭扫描显微镜,使放大倍数又大大地提高。
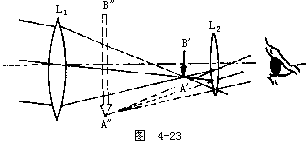
【望远镜】用以观测远处物体或天体的光学仪器。通常的望远镜是由两组胶合透镜构成。每一组胶合透镜都相当一个凸透镜。简单的一种结构:可于一圆筒一端装一个物镜——焦距较长的凸透镜,另一端插入一较小的圆筒,可以自由在大筒中前后移动,小圆筒外端装一目镜——焦距较短的凸透镜,也可作成双筒(即由两个装有物镜和目镜的圆筒构成)。两目镜间的距离可以调节,两筒可使两眼同时观察,从而获得立体感。从远处物体来的光,经物镜折射后造成物体的倒像,将小圆筒伸缩调节,而由目镜将物镜所成的像加以放大,以便观察。用以观察地上远处物体的望远镜有伽利略望远镜、观剧镜、棱镜望远镜等类型,均成正像。用以观测天体的望远镜称天文望远镜,一般均成倒像。按光在望远镜中的路线分,又有折射望远镜(亦称开普勒望远镜)、反射望远镜、双筒望远镜等几种。具有正像透镜装置的折射望远镜亦称“地上望远镜”。本世纪30年代发现天体也发出无线电辐射。用以接收和测量天体无线电辐射的仪器称为射电望远镜,也是天文望远镜的一种。由于开普勒望远镜的镜筒较长,携带不便;故往往在物镜和目镜之间加装一对全反射棱镜,使入射光线在镜筒中经过多次全反射,以减短筒的长度,同时可以将物镜所成的倒像再倒转过来而成正像。这种装置便称为棱镜望远镜,它的视野较大。棱镜望远镜常用于航海、军事窥测和野外观察等。开普勒望远镜的原理如图4-23所示。从远处物体射来的光线,经过物镜L1后,在其焦点以外距焦点很近的地方成一倒立缩小的实像。调节目镜L2与物镜L1的距离使L2的前焦点和物镜的焦点重合,所以实像的A′B′位于L2和它的焦点之间,但距焦点很近的地方,L2以A′B′为物,形成放大的虚像A″B″。这时观测者所看到的就是A″B″。A″B″的视角远大于直接用眼睛看远处物体的视角,因此从望远镜中看到的物体使人觉得离自己既近而又清楚。对于观测天体的天文望远镜,它的聚光本领很大,能看到很远的天体。天文望远镜分为折射式、反射式和折反射式三种。由物镜造成的天体实像可用目镜观测,天文望远镜的口径应尽量大一些,这样进入镜中的光就多一些,所成的像就越明亮清晰,我国最大的天文望远镜口径为2.16米。望远镜种类很多,但基本原理还是光的折射和反射。用其观察远物时,使视角变大。
【射电望远镜】又名“无线电望远镜”。专门用来接收由天体发来的无线电波的仪器。主要由天线和接收机两部分构成。天线用来接收天体发射的无线电波,相当于光学望远镜的物镜。天线类型很多。由许多作为半波振子的金属棒构成的,称为“振子天线”,专用于米波波段无线电波的接收。有的天线则成抛物面形状,称为“抛物面天线”,无线电波的探测器就装在抛物面的焦点上。它主要用于分米、厘米和毫米波波段无线电波的接收。天线和接收机用传输线联接起来。接收机先把由天线传来的高频信号放大,然后加以检滤,再把高频电信号变成可用仪表测量和记录的低频电信号,或变成直接进行照相的图形。因为无线电波可以穿过云雾和尘埃,因此用射电望远镜能不分睛雨昼夜连续进行观测;对于那些难以用光学望远镜观测的天体和宇宙空间,利用射电望远镜便可进行探测研究。
【光的波动说】关于光的本性的一种学说。第一位提出光的波动说的是与牛顿同时代的荷兰人惠更斯。他在17世纪创立了光的波动学说,与光的微粒学说相对立。他认为光是一种波动,由发光体引起,和声一样依靠媒质来传播。这种学说直到19世纪初当光的干涉和衍射现象被发现后才得到广泛承认。19世纪后期,在电磁学的发展中又确定了光实际上是一种电磁波,并不是同声波一样的机械波。19世纪60年代英国物理学家麦克斯韦在理论研究中发现,振动着的电荷或迅速交变的电流都会激起其周围的电磁场,并以波的形式向外传播,其传播速度与光速相同,从而提出光是电磁波的假说。1888年德国物理学家赫兹用实验证明了电磁波的存在,从此奠定了光的电磁理论。这一理论能够说明光的传播、干射、衍射、散射、偏振等许多现象。但不能解释光与物质相互作用中的能量量子化转换的性质,所以还需要近代的量子理论来补充。
【光的微粒说】关于光的本性的一种学说。17世纪曾为牛顿等所提倡。这种学说认为光由光源发出的微粒、它从光源沿直线行进至被照物,因此可以想像为一束由发光体射向被照物的高速微粒。这学说很直观地解释了光的直进及反射折射等现象,曾被普遍接受;直到19世纪初光的干涉等现象发现后,才被波动说所推翻。但在19世纪末和20世纪初,许多有关光和物质相互作用的现象,如光电效应,不能用波动说来解释,这促使爱因斯坦于1905年提出光是一种具有粒子性的实物(光子)。但这观念并不摒弃光具有波动性质。这种关于光的波粒二象性的认识,是量子理论的基础。
【光子】光量子之简称。基本粒子的一种,光子不显电性。光子的能量是量子化的。1905年爱因斯坦在解释光电效应时首次指出了光子的存在,从而揭示了光的波粒二象性。真空中的光子在不同参照系中都以光速c运动。如果光的频率为γ,则光子的能量为hγ(h为普朗克常数,动量为hγ/c,质量为hγ/c2)。但其静止质量为零。
【干涉】发出具有相同频率、相同振动方向和恒定相位差的两列(或两列以上)波在空间迭加时,在交迭区的不同地点加强或减弱的现象。这是波的一个重要特性。波在交迭的区域中,有些地方振动被加强,有些地方振动被减弱,形成明暗相间的“干涉图样”。水波的干涉是常见的现象。单色光波的干涉图样是明暗相间的条纹,复色光产生彩色条纹。利用光的干涉,可以精确地进行长度测量,以及检查表面的平滑程度等。利用电磁波的干涉,可作成定向发射天线。显然声波也可产生干涉。
【光的干涉】两列或多列光波在空间相遇时相互迭加,在某些区域始终加强,在另一些区域则始终削弱,形成稳定的强弱分布的现象。在一般的情况下两个独立光源向空间的一个区域发出光波时不能发生干涉。不发生干涉的两个光源,只说明它们没有发出相干涉。通常的独立光源不相干的原因是:光的辐射一般是由原子的外层电子激发后自动回到正常状态以光的形式把能量放出所形成的。由于辐射原子的能量损失,加上和周围原子的相互作用,个别原子的辐射过程是杂乱无章而且常常中断,持续时间甚短,即使在极度稀薄的气体发光情况下,和周围原子的相互作用已减至最弱,而单个原子辐射的持续时间也不超过10-3秒。当某个原子辐射中断后,它自身或者其他的原子又受到激发重新辐射,但却具有新的初位相。这就是说,原子辐射的光波并不是一列连续不断、振幅和频率都不随时间变化的简谐波,即不是理想的单色光。此外,不同原子辐射的光波波列的初相位之间也是没有一定关系和规律。这些断续、或长或短、初位相不规则的波列的总体,构成了非相干的光波。由于原子辐射的这种复杂性,在不同瞬时迭加所得的干涉图样变化得如此之快和如此地不规则,以致这种短暂的干涉现象无法观测。从微观上看,光子只能自己和自己干涉,不同的光子是不相干的;但是从宏观上看,干涉现象却是大量光子各自干涉结果的统计平均效应。故实际的光的干涉对光源的要求也不是那么苛刻。由于60年代激光的问世,使光源的相干性大大提高,同时快速光电探测仪器的出现,探测仪器的时间响应常数缩短,以至可以观察到两个独立光源的干涉现象。1963年玛格亚和慢德用时间常数10-3~10-9秒的变象管拍摄了两个独立的红宝石激光器发出的激光的干涉条纹。可目视分辨的干涉条纹有23条。对于普通的光源,保证相位差恒定是实现相干的关键。为了解决发光机制中初相位的无规则迅速变化和干涉条纹的形成要求相位差恒定的矛盾,可采用把同一原子所发出的光波分解成两列或几列,使各分光束经过不同的光程,然后相遇,这样,尽管原始光源的初相位频繁变化,分光束之间仍然可能有恒定的相位差,因此可以产生干涉现象。通常用两种方法实现这种分解:(1)分波阵面法——将光源的波阵面分为两部分,使之分别通过两个光具组,经反射、折射或衍射后交迭起来,在一定区域形成干涉。由于波阵面上任何一部分都可以看成为新光源,而且同一波阵面的各个部分有相同的位相,所以这些被分离出来的部分波阵面可作为初相位相同的光源,不论点光源的位相改变得如何快,这些光源的初相位差却是恒定的,杨氏双缝、菲涅耳双面镜和洛埃镜等都是产生这类分波阵面的干涉装置。(2)分振幅法——当一光束投射到两种透明媒质的分界面上,光能一部分反射,另一部分折射。之方法叫做分振幅法。最简单的分振幅干涉装置是薄膜,它是利用薄膜的上下表面对入射光反复地反射,由这些反射光波在空间相遇而形成的干涉现象。由于薄膜的上下表面的反射光来自同一入射光的两部分,只是经历不同的路径而有恒定的相位差,因此它们是相干光。另一种重要的分振幅干涉装置,是万克耳孙干涉仪。光的干涉现象是光的波动性的最直接、最有力的实验证据。光的干涉现象是牛顿微粒模型根本无法解释的,只有用波动说才能圆满地解释这一现象。
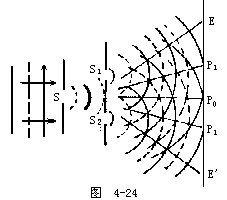
【杨氏干涉实验】杨格于1801年设法稳定两光源之相位差,首次做出可见光之干涉实验,并由此求出可见光波之波长。其方法是,使太阳光通过一挡板上之小孔使成单一光源,再使此单一光源射到另一挡板上,此板上有两相隔很近的小孔,且各与单光源等距离,则此两同相位之两光源在屏幕上形成干涉条纹。因为通过第二挡板上两小孔之光因来自同一光源,故其波长相等,并且维持一定的相位关系(一般均维持同相),因而能在屏幕上形成固定不变的干涉条纹。若X为屏幕上某一明(或暗)条纹与中心点O的距离,D为双孔所在面与屏幕之间的距离,2a为两针孔S1,S2间之距离(通常小于1毫米),λ为S光源及副光源S1、S2所发出的光之波长。两光源发出的两列光源必然在空间相迭加,在传播中两波各有各的波峰和波谷。当两列波的波峰和波峰或波谷和波谷相重叠之点必为亮点。这些亮点至S1与S2的光程差必为波长λ的整数倍。在两列波的波峰与波谷相重叠之点必为暗点,这些暗点至S1与
![]()
涉条纹如图4-24所示,它是以P0点为对称点而明暗相间的条纹。P0点处的中央条纹是明条纹。当用不同的单色光源作实验时,各明暗条纹的间距并不相同。波长较短的单色光如紫光,条纹较密;波长较长的单色光如红光,条纹较稀。另外,如果用白光作实验,在屏幕上只有中央条纹是白色的。在中央白色条纹的两侧,由于各单色光的明暗条纹的位置不同,形成由紫而红的彩色条纹。干涉明暗条纹的条件由图4-25所示,设相干光源S1与S2之间的距离为2a,到屏幕E的距离为D,已知D>>2a。在屏幕上任取一点P,P距S1与S2的距离分别为r1与r2。从S1与S2所发出的光,到P点处的光程差是:
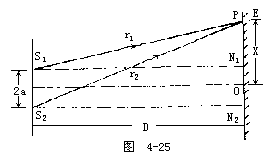
δ=r2-r1
设N1和N2分别为S1和S2在屏幕上的投影点,O为N1和N2的中点,并设OP=x。从图中直角三角形S1PN1和S2PN2,可知
![]()
![]()
两式相减后,得
![]()
因D>>2a,所以r2+r1≈2D,因此
![]()
如果P为一亮点,按干涉条件,光程差应等于波长的整数倍,
即
![]()
或
![]()
这里K=0相应于在O点处的中央明条纹。K=1,K=2,…等等相应的明条纹分别称为第一级、第二级、…明条纹。如果P点为暗点,按干涉条件,有
![]()
![]()
由此可知某明(暗)条纹与中点O的距离与光之波长及光源到屏幕的距离成正比,与二针孔间的距离成反比。依此公式可计算某光波波长的近似值。
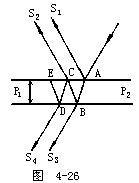
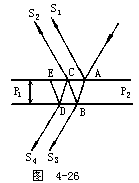
【薄膜干涉】水面上的薄层油膜,机动车在潮湿柏油道上所遗留下来的油迹,或是肥皂泡等,都会在白光中出现灿烂的彩色。所有上述的各例中,均是由薄膜干涉现象引起的。若将一用金属细丝制成的矩形框架,浸以肥皂水形成一层薄膜,然后用弧光灯的白光或阳光照射于其上,就呈现出典型的薄膜干涉。其中一部分是由反射光产生的干涉条纹,而其余的则从皂液膜中透过去。此时从反射光中可以看到许多与水平框架上缘平行的彩色横条纹。不但如此,这些横条纹还会慢慢地向下移动,愈靠近框架上缘则愈宽。此外,透射光在白幕上也显示出许多彩色横条纹,但比起反射光中的条纹要暗淡得多。如果用单色光代替白光,则彩色现象会立即消失,而出现的便是一些彩色条纹的花样类似于明暗相间的条纹。在1800年英国科学家杨格指出薄膜彩色条纹之形成,是因为干涉现象所致。如图4-26,SA是一束单色光,斜射到厚度为d之皂液薄膜P1P2上。照射于A处之光线S(实际上它代表的是一个光束),一部分立即被反射,而另一部分则折射到B处。反射部分以S1来表示,折射至B处者又会照样地有一部分立即被反射,及另一部分被折射。后者仍用S3来表示。被反射的光线抵达C处,又在该处分为两部分,一部分折射为平行于S1之S2,另一部分被反射后则沿CD路线而抵达D处。然后再在该处被分为两部分,一部分折射为平行于S3之S4,另一部分则被反射到E处。关于薄膜上所发生之干涉现象(单色光),如果有两条平行入射到薄膜上,如图4-27中的a和b,b在薄膜上表面的反射光线为b1,a由膜的上表面折射到下表面的C点再反射到B点,又折回a1与b1重合。我们可以计算出aa1和bb1之间的光程差。对薄膜来说,AB的长度比光源S到薄膜的距离小得很多,因此∠BSA非常小,可以认为SA和SB是相互平行的。作AD⊥SB,可以认为SA=SD,也就是说从S发出的这两条光线分别到达A点和D点时,光程是相等的。从图中可以看出,光线a在薄膜(折射率为n2)中经历路程ACB到达B点,而光线b在原媒质(折射率n1<n2)中经历路程DB而在B点反射。所以这两光线之间的光程差
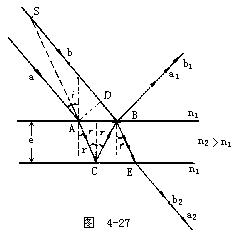
![]()
![]()
的,而光线a在c处是在光疏媒质面上反射的,两者之间有了附加的半波长光程差的缘故,从图上可以看出
![]()
式中e为薄膜厚度,r为折射角。根据折射定律n1sini=n2sinr,因此
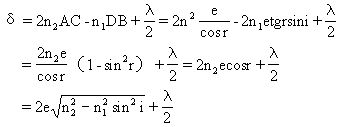
于是,干涉条件是
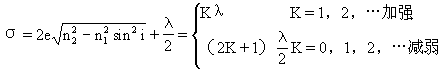
![]()
(e到处一样)来说,光程差是随光线的倾角(指入射角i)而改变的。如果用发散的单色光线束照射在厚度均匀的平面薄膜上,相当于每一入射角i都有一束平行光入射,那么,具有同一倾角的一切光线将有同一光程差。这样,不同的干涉明条纹和暗条纹,相应地具有不同的倾角,而同一干涉条纹上的各点都具有同一的倾角,因此这种干涉条纹叫做等倾干涉条纹。对于透射光来说,也有干涉现象。这时,光线b,是由光线b直接透射而来的,而光线a2是由光线a折入薄膜后在C点和B点处经两次连续反射后再透射出来的,这两次反射均在光疏媒质面上发生,所以不存在反射时的半波损失,因此,这两束透射的相干光的光程差是
![]()
由此可见当反射光相互加强时,透射光将相互减弱;当反射光相互减弱时,透射光将相互加强。
【光程】光在媒质中通过的路程和该媒质折射率的乘积。例如,在折射率为n的介质中,光行进一距离d,光程即为乘积nd,由n的物理意义可知,光在该介质中行经距离d所需的时间,与光在真空中行经nd距离所需的时间相等。这是因为,媒质的折射率等于真空中的光速和媒质中的光速之比,所以光程也就是在相同的时间内光在真空中通过的路程。显然,当光在折射率为n1、n2、…的各介质中行程各为d1、d2…,则光程为
d=n1d1+n2d2+…=Σnidi
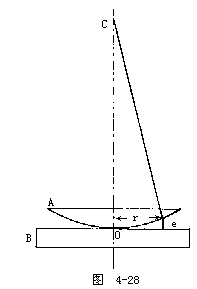
【牛顿环】又称“牛顿圈”。光的一种干涉图样,是一些明暗相间的同心圆环。例如用一个曲率半径很大的凸透镜的凸面和一平面玻璃接触,在日光下或用白光照射时,可以看到接处点为一暗点,其周围为一些明暗相间的彩色圆环;而用单色光照射时,则表现为一些明暗相间的单色圆圈。这些圆圈的距离不等,随离中心点的距离的增加而逐渐变窄。它们是由球面上和平面上反射的光线相互干涉而形成的干涉条纹。在加工光学元件时,广泛采用牛顿环的原理来检查平面或曲面的面型准确度。图4-28为牛顿环的示意图,B为底下的平面玻璃,A为平凸透镜,其与平面玻璃的接触点为O,在O点的四周则是平面玻璃与凸透镜所夹的空气气隙。当平行单色光垂直入射于凸透镜的平表面时。在空气气隙的上下两表面所引起的反射光线形成相干光。如图中所示。光线在气隙上下表面反射(一是在光疏媒质面上反射,一是在光密媒质面上反射)。形成两相干光线,这两光线之间的光程差是
![]()
所以
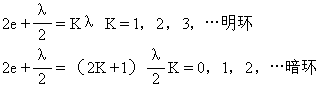
现在我们求与O相距r处的空气层厚度e,由图中的直角三角形得
r2=R2-(R-e)2=2Re-e
因R>>e,所以e2<<2Re,可将e2从式中略去,于是
![]()
上式说明e与r2成正比,所以离开中心愈远,光程差增加愈快,所

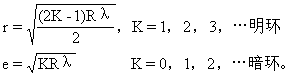
【半波损失】光在被反射过程中,如果反射光在离开反射点时的振动方向对入射光到达入射点时的振动方向恰好相反,这种现象叫做半波损失。从波动理论知道,波的振动方向相反相当于波多走(或少走)了半个波长的光程。入射光在光疏媒质中前进,遇到光密媒质界面时,在
![]()
程中产生半波损失,这只是对光的电场强度矢量的振动而言。如果入射光在光密媒质中前进,遇到光疏媒质的界面时,不产生半波损失。不论是掠射或垂直入射,折射光的振动方向相对于入射光的振动方向,永远不发生半波损失。
【全息照相】一种记录被摄物体反射(或透射)光波中全部信息(振幅、相位)的新型照相技术。普通的照相利用透镜成像原理,在感光胶片上记录反映被摄物体表面光强变化的平面像。全息照相不单是记录了被摄物体的反射光波强度(振幅),而且还记录了反射光波的位相。通过一束参考光束和一束被摄物体上的反射光束在感光胶片上迭加而产生干涉现象,可以实现上述的目的。参考光束与反射光束都是从一束相干性极好的激光束分离出来的。感光胶片上记录的干涉图样极为错综复杂,这样的图样称为全息图。由全息图看不出原来被摄物体的表观图像,但是当再用一束激光(或单色光)照射这全息图时,可以透过全息图而看到原物体的具有立体感的形像。这是因为光束经过全息图后又模拟出与原来物体相同的反射光波,这种重构光波状态的效应称为波前重建。全息照相在讯息记录、形变计量等方面有较多的应用。
【光的衍射】光绕过障碍物偏离直线传播而进入几何阴影,并在屏幕上出现光强不均匀分布的现象。这种现象也体现了光的波动特征。光的衍射现象是光的波动性的最直接,最有力的实验证据。牛顿的微粒模型难以说明光绕过障碍物时发生的弯曲现象,衍射现象只能用波动说解释。根据惠更斯一菲涅耳原理,不仅可以对光绕过障碍物边缘偏离直线传播的现象作一般性的解释,而且能定量分析衍射图样的发光强度分布。光屏上任意一点的发光强度可根据次波迭加推算出来。因此光的衍射现象是光的波动性的最直接、最有力的证据。如图4-29所示,K是一可以调节的狭缝。从光源S发出的光线,穿过K后,在屏幕E上呈现光斑ab。在S、K、E三者的位置已经固定的情形下,ab的宽度是由缝的宽度决定的。当狭缝从一定的宽度逐渐缩小时,穿过缝的光束也逐渐变窄,在屏幕E上的光斑ab随之变窄,但是当缝K缩小到一定程度时,屏幕上的光斑不仅不变窄,反而增宽,如图中a′b′所示。而且光斑的全部亮度也将发生变化,由原来的均匀分布变成一系列明暗条纹。光斑的边缘也将失去明显的界限,变得模糊不清。应当指出。在图4-29中所示的衍射实验装置中,狭缝距光源和屏幕都很近,所以入射光和衍射光均是非平行光束。在光学中,通常把入射光或衍射光不是平行束的衍射,称为菲涅耳衍射。图4-29所示的单缝衍射情况就是一种菲涅耳衍射。在另一些装置中,如果入射光和衍射光都是平行光束,那末,这种衍射称为夫琅和费衍射。显然,观察这种绕射现象需要利用透镜。
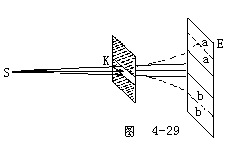
【单缝衍射】单缝衍射的实验装置(夫琅和费单缝衍射)如图4-30所示。光源S放在透镜L1的主焦面上,因此通过透镜L1后的光线是一平行光束。这束平行光照射在很窄的单缝K上,一部分穿过单缝,再经过透镜L2在屏幕E上将出现衍射条纹的像。实验指出,平行光(波阵面和透镜的光轴相垂直)经过透镜后,会聚在焦面中间的光线相互加强而产生亮条纹,这就证明,周相相同的平行光线,经过透镜而被聚焦时,它们的周相仍然是相同的。故可认为透镜的存在不引起附加的周相差。图4-31所示为单缝衍射的说明图。设有宽度为a原单缝,在平行单色光的垂直照射下,位于单缝所在处的波阵面AB上的子波沿各方向传播。衍射角(衍射后的平行光束与入射平行光束所成的角)为j的一束平行光经过透镜后,聚焦在屏幕上P点。这种光线的两条边缘光线之间的光程差为
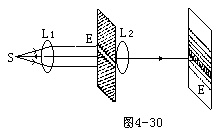
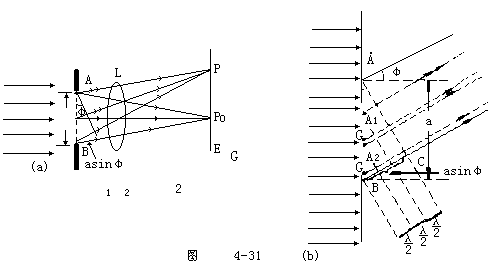
BC=asinj
P点条纹的明暗完全决定于光程差BC的量值。菲涅耳在惠更斯—菲涅耳原理的基础上,提出了将波阵面分割成许多等面积的波带的方法。在单缝的例子中,可以作一些平行于AC的平面,使两相邻平面之间的
![]()
分成AA1、A1A2、A2B等整数个波带。由于各个波带的面积相等,所以各个波带在P点所引起的光振幅接近相等。两相领的波带上,任何两个对应点(如A1A2带上的G点与A2B带上的G′点)所发出的光线的
![]()
加周相差,所以到达P点时周相差仍然是π,结果任何两个相邻波带所发出的光线在P点将相抵消。由此可见,BC是半波长的偶数倍时,即对应于某给定角度j,单缝恰好能分成偶数个波带时,所有波带的作用成对地相互抵消,在P点处将出现暗条纹;如果
BC是半波长的奇数,亦即单缝可分成奇数个波带时,在P点处将出现明条纹。上述结果可用数学式表示为,当j适合
-λ< asinj<λ
时为零级明条纹,当j适合
![]()
时为暗条纹,当j适合
![]()
时为明条纹。从K=1,2,3,…分别得到第一级、第二级、…等明条纹或暗条纹。应当指出,对任意衍射角j来说,AB一般不能恰巧分
![]()
焦后,形成屏幕上亮度介于最明和最暗之间的中间区域。
【衍射光栅】衍射光栅简称光栅。利用光的多缝衍射原理使光发生色散的光学元件。它是在一块平面(或凹面)玻璃或镀有金属的反射面上刻上大量相互平行、等宽、等距的刻痕。平面的称为平面的光栅,凹面的称为凹面光栅。平面光栅又可根据所用的是透射光还是反射光而分为透射光栅和反射光栅两种。通常用塑料在做为母模的光栅上复制出与原刻线完全一样的薄膜,把它贴在玻璃片上,制成所谓“复制光栅”或“摹拟光栅”。最新的光栅是利用全息照相方法制做的,叫做“全息光栅”。全息光栅比用机械刻划的光栅的条纹更密,条纹间隔误差更小,因此在很大的应用范围里,刻划光栅逐渐为全息光栅所取代。光栅每单位长度内的刻痕多少,主要决定于所要分光的波长(两刻痕间的距离应与该波长同一数量级),单位长度内刻痕越多,它的色散率越大。而光栅的分辨本领则决定于刻痕的总数。天然晶体内按一定规则排列的微粒,形成所谓“空间光栅”(两微粒间距离比人工刻出来的痕距要小得多),它适用于对X射线的衍射。当一束平行单色光垂直照射在光栅上,光线经过透镜L后,将在屏幕E上呈现各级衍射条纹。图4-32是光栅实验的原理。精制的光栅,在1厘米内刻痕可以多达数万条。图中S是和纸面垂直的线光源,它们于透镜L1的焦平面上,屏幕DD放在透镜L2的焦平面上。在两透镜之间是一块由一系列等宽等间隔的平行狭缝构成的光栅。设各缝的宽度都等于a,相邻两缝间不透明的部分的宽度都等于b。则a+b=d称为“光栅常数”。由光源S发出的光通过L1而出射的平行光照射在光栅上。对光栅中每一狭缝来说,均有单缝衍射的结果,由于光栅中有大量的等面积的平行狭缝,所以最后结果并不是每个单独的狭缝所起的作用,这时最重要的作用来自各个狭缝所发出的光波之间的干涉。即使在某一给定方向上,按单缝衍射将得到明条纹,但由于缝与缝之间光波的相互干涉,最后可能得到暗条纹。因此,光栅的衍射条纹应看作是衍射与干涉的总结果。查衍射角j适合条件
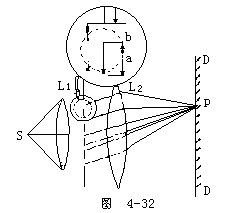
![]()
时,由所有相邻狭缝的相应位置射出的光线的光程差是波长的整数倍,因而相互加强形成明条纹。显然,光栅上狭缝的条数愈多,条纹就愈为明亮。上式中k是整数,表示明条纹的级数。而当j角适合条件
( ![]()
时,将出现暗条纹。当j角适合条件
![]()
时,由各个狭缝所射出的光波都将各自地由于干涉而抵消,形成暗条纹。当然也就谈不上缝与缝之间的干涉作用,在这里即使符合明干涉条纹条件的也没有明条纹出现。由此可见在光栅衍射中,仅当j角满足(a+b)
![]()
景,对给定的入射单色光波来说,光栅上每单位长度的狭缝条数愈多,亦即光栅常数a+b愈小,各级明条纹的间隔也愈大,因为这时的j角要大。光栅上狭缝总数愈多透射光束愈强,因此所得明条纹也愈亮。由于这些优点,通常用衍射光栅可以准确地测量光的波长。
【分辨本领】仪器或肉眼对两个非常靠近的物点或量值刚能加以识别的能力。随着仪器和所要分开的量值性质不同,分辨本领有不同的衡量方法。(1)在光学仪器如显微镜中,以它所能分辨的物体上两个最靠近的细点间距离作为分辨本领;但在望远镜和肉眼中,则以它们对两物点的视角来量度。目前一般的光学显微镜的分辨本领可达2×10-5厘米,电子显微镜可达2~3×10-8厘米;望远镜的理论分辨本领可达0.03秒(实际分辨本领受观察地点的大气条件影响,一般要比理论分辨本领小),人的眼睛分辨本领约为1分。(2)光谱仪的分辨本领为两条刚能分辨的光谱线的波长平均值对它们波长差的比值。比值越大分辨本领越高。各种“能谱仪”的分辨本领可用类似的定义来表示。也有以这种定义的倒数来表示的(如β谱仪),称为“分辨率”。(3)成像系统(如照相、电视等)的分辨本领通常以某一规定长度内能够分辨的平行直线数表示,线数越多,分辨本领越大,成像就越清晰。在电视系统中分辨本领常称为分解力。
【光的电磁说】说明光在本质上是电磁波的理论。电磁辐射不仅与光相同,并且其反射、折射以及偏振之性质也相同)由麦克斯韦的理论研究表明,空间电磁场是以光速传播,这一结论已被赫兹的实验证实。麦克斯韦,在1865年得出了结论:光是一种电磁现象。按照麦克斯韦的理论
![]()
式中c为真空中的光速。v为在介电常数为ε和导磁系数为μ的媒
![]()
![]()
这个关系式给出了物质的光学常数,电学常数和磁学常数之间的关系。当时从上述的公式中看不出n应随着光的波长λ而改变,因而无法解释光的色散现象。后来罗仑兹在1896年创立了电子论,从这一理论看,介电常数ε是依赖于电磁场的频率,即依赖于波长而变的,从而搞清了光的色散现象。光的电磁理论能够说明光的传播、干涉、衍射、散射、偏振等许多现象,但不能解释光与物质相互作用中的能量量子化转换的性质,所以还需要近代的量子理论来补充。
【红外线】亦称“红外光”。在电磁波谱中,波长介于红光和微波间的电磁辐射。在可见光的范围以外,波长比红光要长,有显著的热效应,可以用温差电偶、光敏电阻等仪器来测量,波长在0.77~3微米为近红外区;3~30微米为中红外区;30~1000微米为远红外区。红外线容易被物体吸收,转化为物体的内能;在通过云雾等充满悬浮粒子的物质时,不易发生散射,具有较强的穿透能力,红外线应用很广,可用以焙制食品、烘干油漆以及进行医疗等。物质对红外线的吸收光谱对研究物质的分子结构、化学分析及化学工业上的控制有重要意义。军事上常用红外探测器来探测目标,以及红外通信等。
【紫外线】亦称“紫外光”。在电磁波谱中位于紫光和伦琴射线(X射线)之间的电磁辐射。波长约为(4~39)×10-6厘米,不能引起视觉(即在可见光范围之外)。可见光能透过的物质,对于紫外线的某些波段却会强烈的吸收。例如:玻璃对波长小于35×10-4厘米的紫外线有强烈的吸收;地球大气中的氧和臭氧几乎全部吸收了太阳辐射中,波长小于29×10-6厘米的紫外线;水晶(即石英)吸收波长小于2×10-5厘米的紫外线;波长小于2×10-5厘米的紫外的线被空气强烈吸收。因此观察这一紫外线波段的光谱仪的内部必须抽成真空,这个波段称为真空紫外,适用于这一波段的光谱仪称为真空紫外光谱仪。水银灯和电弧的光中有(25~39)×10-6厘米之间的强紫外辐射,是常用的紫外线光源,紫外线通常用光电元件和感光乳胶来检测。紫外光谱是研究原子结构的重要手段,紫外线在工农业方面也有重要应用价值。在生物学和医学上常用紫外线进行杀菌消毒,诱发突变、治疗皮肤病和软骨病等。
【伦琴射线】又称“X射线”,它是一种波长很短的电磁辐射,其波长约为(20~0.06)×10-8厘米之间。伦琴射线具有很高的穿透本领,能透过许多对可见光不透明的物质,如黑纸、木料等。这种肉眼看不见的射线可以使很多固体材料发生可见的荧光,使照相底片感光以及空气电离等效应,波长越短的X射线能量越大,叫做硬X射线,波长长的X射线能量较低,称为软X射线。当在真空,高速运动的电子轰击金属靶时,靶就放出X射线,这就是X射线管的结构原理。放出的X射线分为两类:(1)如果被靶阻挡的电子的能量,不越过一定限度时,只发射连续光谱的辐射。这种辐射叫做轫致辐射;(2)一种不连续的,它只有几条特殊的线状光谱,这种发射线状光谱的辐射叫做特征辐射。连续光谱的性质和靶材料无关,而特征光谱和靶材料有关,不同的材料有不同的特征光谱这就是为什么称之为“特征”的原因。X射线的特征是波长非常短,频率很高。因此X射线必定是由于原子在能量相差悬殊的两个能级之间的跃迁而产生的。所以X射线光谱是原子中最靠内层的电子跃迁时发出来的,而光学光谱则是外层的电子跃迁时发射出来的。X射线在电场磁场中不偏转。这说明X射线是不带电的粒子流。1906年,实验证明X射线是波长很短的一种电磁波,因此能产生干涉、衍射现象。X射线用来帮助人们进行医学诊断和治疗;用于工业上的非破坏性材料的检查;在基础科学和应用科学领域内,被广泛用于晶体结构分析,及通过X射线光谱和X射线吸收进行化学分析和原子结构的研究。
【电磁波谱】在空间传播着的交变电磁场,(即电磁波)。它在真空中的传播速度约为每秒30万公里。无线电波、红外线、可见光、紫外线、X射线、γ射线都是电磁波,不过它们的产生方式不尽相同,波长也不同,把它们按波长(或频率)顺序排列就构成了电磁波谱。依照波长的长短以及波源的不同,电磁波谱可大致分为:(1)无线电波——波长从几千米到0.3米左右,一般的电视和无线电广播的波段就是用这种波;(2)微波——波长从0.3米到10-3米,这些波多用在雷达或其它通讯系统;(3)红外线——波长从10-3米到7.8×10-7米;(4)可见光——这是人们所能感光的极狭窄的一个波段。波长从(78~3.8)×10-6厘米。光是原子或分子内的电子运动状态改变时所发出的电磁波。由于它是我们能够直接感受而察觉的电磁波极少的那一部分;(5)紫外线——波长从3×10-7米到6×10-10米。这些波产生的原因和光波类似,常常在放电时发出。由于它的能量和一般化学反应所牵涉的能量大小相当,因此紫外光的化学效应最强;(6)伦琴射线——这部分电磁波谱,波长从2×10-9米到6×10-12米。伦琴射线(X射线)是电原子的内层电子由一个能态跳至另一个能态时或电子在原子核电场内减速时所发出的;(7)γ射线——是波长从10-10~10-14米的电磁波。这种不可见的电磁波是从原子核内发出来的,放射性物质或原子核反应中常有这种辐射伴随着发出。γ射线的穿透力很强,对生物的破坏力很大。
【分光镜】可产生并观察光谱的仪器,故又称分光仪。也可以用来作简单的波长测量仪器。分光镜的型式很多,各型式间除操作原理的差异外,还有被探测的辐射线不同,辐射频率的区间由红外光到伦琴射红(X光)。一种简单的分光镜就是:从光源S射出的光,经过一狭缝,变成一窄束光后,由凸透镜而变成平行光(窄缝应处在凸透镜的焦平面内),使平行光经过一棱镜而色散,因同色光(同波长)的射线平行,这些光线再通过一凸透镜时则可把各色光发别聚焦在屏幕的不同位置上,于是在屏幕上就呈现出一排按照波长长短排列的彩色的光谱,这就是光源发出的光谱,不同元素的光源它的光谱也各不相同。现在的分光镜中多数都用衍射光栅代替棱镜。如果光栅的表面是凹面的(凹面光栅),这种光栅本身就有聚焦作用,因此可以取消透镜系统。
【发射光谱】由物体发光直接所产生的光谱叫做发射光谱。如物质在高温状态或因受到带电粒子的撞击而激发后而直接发出的光谱均属发射光谱。由于物质被激发时所处的状态不同,发射光谱有不同的组合形式;如原子被激发后发出明线光谱;分子则有带光谱,实际上是一组非常密集的线光谱组成;在炽热的固态、液态或高压气体中为连续光谱。例如,稀薄气体发光是由不连续的亮线组成的,这种发射光谱就是明线光谱,也就是原子光谱。因为原子有一系列分立的能级,电子从能量较高的激发状态跃迁到能量较低的激发态或基态时,以一定频率的光的形式放出能量。其发光频率由
hv=E2-E1
确定。对于不同的E1和E2,有不同的能量差。或者说,电子在不同能级之间的跃迁将产生不同频率的光谱线。不同的原子具有一系列不同的能级,正如每个人有他独特的指纹一样。因此不同的原子有不同的发射光谱线系。通过测定光谱线系的波长能鉴定发光的原子是何种元素。波长连续分布的光谱叫做连续光谱。炽热的固体、液体、高压气体往往发出连续光谱。电子和离子复合时,以及高速运动的带电粒子在加速场中运动时,也能发射这种光谱。参见“轫致辐射”。
【吸收光谱】当物体发出的波长连续分布的光通过物质时,某些波长的光被物质有选择性地吸收,它所产生的光谱是在连续光谱的背景下,分布着一系列暗线或暗带。这种光谱叫做吸收光谱。由于物质所在的状态不同,吸收光谱有不同的形状;如原子状态的吸收光谱中有比较分开的暗线光谱;气体或蒸气的分子状态的吸收光谱是由密集的暗线组成的暗带光谱;处于固体或液体状态中的物质,则往往将一定波长区域的光线吸收,而表现出逐渐变暗的一些暗带。在一般情况下,物质吸收光谱的波长与该物质的某些发射光谱波长相对应。因为发射光谱一般必须在高温下获得,而高温下的分子或晶体往往是易于分解,因此吸收光谱最适宜于研究分子的结构。又由于分子的振动和转动光谱均位于红外区域,所以红外吸收光谱是研究分子结构变化的重要手段。
【光谱分析】应用光谱学的原理和实验方法以确定物质的结构和化学成分的分析法。炽热的气体或蒸气能产生特定的光谱线,人们可以根据分析所产生的这些谱线来确定此种气体中的物质成分。从各种星球的光谱中,可以推断其上所存在之元素与物质。由于极微量的元素存在足以在光谱中产生特征谱线,所以此种分析在化学中价值很大。许多元素,如铯与铷等,就是由光谱分析发现的。光谱分析包括:(1)发射光谱分析——利用各种物质的特征发射光谱以确定其化学成分。按目的和方法不同又可分为:①光谱定性分析。因每种元素都有各自的特征谱线,可从待测物质所发射的光谱,鉴定其中所含的元素。②光谱定量分析。因每种元素所发射的特征谱线的强度,与它在物质中的含量有关,所以可通过谱线强度的对比,测定物质中各元素含量的多少。(2)吸收光谱分析——利用各种物质的特征吸收光谱以确定其结构的化学成分。例如分光光度分析。根据特征光谱的波长不同,分为“可见和紫外分光光度分析法”及“红外分光光度分析法”。适用于可溶性物质的分析。光谱分析具有极高的灵敏度和准确度、且分析速度快,故在生产技术(如冶金、地质、化工,石油等部门)中广泛采用。
【光谱仪】将复色光分解为光谱,并进行记录的精密光,学仪器。在可见光和紫外光区域,过去常用照相法记录光谱,故也称摄谱仪。在红外区域,一般用光敏或热敏元件逐点记录,故有红外分光计的名称。现在在各个波段均采用光电接收和记录的方法,比较直接、灵敏,称为“光电记录光谱仪”。为了得到更多的光谱线,可以把被分析物质放在等离子体火焰中激发,在光谱仪中除采用光电接收方法外,还配有专用计算机,计算物质中各元素含量。可以在数秒种内从显示器的荧光屏读出结果。这种仪器称为“等离子体光电直读光谱仪”简称ICP光谱仪,是当前光谱分析中最迅速最灵敏的一种仪器。光谱仪是上述各种仪器的总称。虽然各种光谱仪的形式各异,但均有三大主要部分:一是激光光谱的光源;二是光谱仪系统,使不同波长的光聚焦在仪器上的特定位置。三是用置于焦点上的探测器来量光的强度。近代的光谱仪大都采用微型计算机处理实验结果。
【激光】用电学、光学及其它方法对工作物质进行激励,使其中一部分粒子激发到能量较高的而又能维持时间较长的所谓亚稳态上去,当这种状态的粒子数量大于能量较低状态的粒子数时,叫做粒子数的反转。由于场效应的作用,处于高能态的粒子受到感应而跃迁到低能态,同时发生光的辐射,这种辐射称为受激辐射。这种辐射又感应其他高能态的粒子发生同样的辐射。受激辐射的特点是辐射光和感应它的光子同方向、同位相、同频率并且同偏振面。若把激光的工作物质置于谐振腔内,则光辐射在谐振腔内沿轴线方向往复反射传播,多次通过工作物质,使工作物质中处于反转态的粒子不断受到感应而发光,一个粒子的辐射感应一大片造成雪崩似的放大效果,而形成一束强度很大、方向集中的光束,这种光束称之为激光。激光的特点是:具有很好的单色性、方向性和相干性,并且亮度极高。(1)单色性——如氦氖激光器发射出频率为4.74×1014赫兹的红色激光,它的频带宽仅是9×10-2赫兹。(2)方向性——激光光源的光束延伸几公里后扩展范围的线度不到几厘米,而探照灯延伸几公里后的扩展范围的线度有几十米。(3)相干性——受激辐射满足干涉条件,因而激光具有很好的相干性。(4)高亮度——由于激光能把巨大的能量高度集中地辐射出来。如果把强大的激光束会聚起来照射到物体上,可以使物体的被照部分在不到千分之一秒时间内产生几千万度的高温。自从激光问世以来,不但使古老的光学又变得生气勃勃,并促使许多科学技术领域发生了巨大的变化,诸如激光手术刀,激光切割,直至激光武器等等。
【光电效应】物质(主要指金属)在光的照射下释放出电子的现象,称之为光电效应。其所释放出的电子叫做“光电子”。1887年德国物理学家,赫兹首先发现,这种效应不能简单地用光的波动理论来解释,1905年爱因斯坦引入光子概念才满意地说明了这一现象。根据爱因斯坦的理论,当光照射到物体上时,光子的能量可被物体中某个原子的外层电子全部吸收。如果电子吸收的能量hv足够大,使它不但具有足以摆脱原子束缚它的能昨(即电离能量)I,而且还有能量用于脱离物体表面所需的逸出功(或叫做功函数)W,则电子就可以从物体表面税逸出来,成为光电子,这就是光电效应的过程爱因斯坦方程是
![]()
![]()
内部有大量的自由电子,这些自由电子不需要克服脱离原子的电离能量,因而对金属来说,I可以略去,爱因斯坦方程成为
![]()
如果hv<W,电子就不能脱出金属的表面。对于一定的金属,产生光电效应的最小光频率(极限频率)v0由
hv0=W
确定。相应的红限波长为
![]()
由此可见,光电效应只有在照射物体的光频率大于某个确定值时,物体才能发出光电子,这个频率就是v0,相应的波长λ0通常称为红限波长。不同的物质具有不同的极限频率v0和相应的红限波长λ0。被照物体发射的光电子数和照射光的强度成正比。光电子脱出物体时的初始动能只和照射光的频率有关而与发光强度无关。从实验中还得知,产生光电流的过程非常快,一般不超过10-9秒;光照射停止,光电流也就立即停止。这表明光电效应是瞬时的。利用光电效应可以制造光电倍增等。光电倍增管能将一次次闪光转换成一个个放大的电脉中,然后送到电子线路中,被记录下来。大多数纯金属材料的逸出功约在2~6电子伏特之间或大一些。这表明其红限波长要小于4×10-5厘米,可见,可见光对这些物质不能产生光电效应。高效率的光电效应材料,除逸出功应较低外,还需具有能将大部分照射光吸收,并能更多地将它转变为电子动能的特性,所以反射性高及透明的物质不是理想的光电效应材料。碱金属钠、钾等物质是极好的光电效应材料。其中钾的逸出功为2eV(电子伏特),钠的逸出功为2.3eV。
【光的波粒二象性】光电效应和康普顿效应,使人们无法不承认光的量子性质,而干涉和衍射现象又使人们不能放弃光的波动性。把光的两重性质——波动性和微粒性联系起来,即动量和能量是光的粒子性的描述,而频率和波长则是波的特性。虽然普朗克和爱因斯坦的理论揭示出光的微粒性,但这并不否定光的波动性,因为光的波动理论早已被干涉、衍射等现象所完全证实。这样光就具有微粒和波动的双重性质,这种性质便被称为光的波粒二象性。1925年玻恩提出的波粒二象性的统计解释,把波动性和粒子性联系起来。这种统计的观点,统一了粒子概念和波动概念。一方面它具有集中的能量、质量和动量,也就是光的粒子性;同时在另一方面,它们在各处出现,具有一定的几率,由这个几率可以算出它们在空间的分布,这种空间分布又和波动的概念一致。必须注意的是,光子既不是经典的波,也不是经典的粒子,更不是两者的混合。其实当光子和物质相互作用时,它是粒子;当它在运动时,观察到衍射现象来说,它是波动。但它究竟是什么,很难用经典物理学的概念来完全描述。真正把光的波粒二象性统一地反映出来的理论是量子电动力学,它是在量子力学的基础上建立起来的。不仅光具有波粒二象性,而且电子、原子等一切实物粒子也都具有两重性。且一个动量为P、能
![]()
粒子运动方向传播的平面波(h为普朗克常数)。这种对微观粒子所具有波动性的描述,叫做物质波,即德布罗意波。但是不能因此而忽视光子和电子、原子等实物粒子之间的差别。例如,就速度方面,光在真空中的传播速度只有一个不变的速度,即光速c,而电子可以有小于光速的任何速度;在质量方面电子有静止质量,而光子的静止质量等于零。尽管如此,电子和光子之间仍然有着内在联系。当能量超过1.02MeV(兆电子伏特)的光子,在经过另一粒子(通常是原子核)附近时,就可转化为电子对。反之当电子和正电子相遇时,电子对将湮没而转化为两个光子,这一现象揭示了光子和电子有着深刻的联系,它也说明了物质存在形式之间的相互转化。德布罗意的假逆,通过能量和动量,把微观粒子的粒子性和波动性联系起来,即
E=mc2=hv
![]()
所以对具有静止质量m0的实物粒子来说,按照德布罗意假说,粒子以速度v运动时,相应于这些粒子的平面单色波的波长是
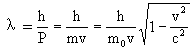
上述公式称为德布罗意公式,如果v<<c,则
![]()
以电子为例,电子经电场加速后,电子的速度将由关系式
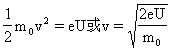
式中U为加速电位差,所以
![]()
将h=6.62×10-34〔焦耳〕〔秒〕,e=1.60×10-19〔库仑〕,m0=9.11×10-31〔公斤〕代入上式,得
![]()
如果V=15O伏特的电位差,则德布罗意波的波长λ=10-8米。如果电位差再大则λ也相应变短。
【普朗克】德国物理学家。1900年为了克服经典物理学对黑体辐射现象解释上的困难,创立了物质辐射(或吸收)的能量只能是某一最小能量单位(能量量子)的整数倍的假说,即量子假说,对量子论的发展有重大影响。在热力学和统计物理学方面,如关于热力学定律的表述、非平衡态理论等,都有一定贡献。
【普朗克常数】物理学中普适常数之一,以符号h表示,其数值为6.62×34-34焦耳·秒。这一常数是1900年普朗克在研究黑体辐射时首次引进的。当时他为了推导出一个与实验结果相符合的黑体辐射公式,普朗克把黑体辐射看作是带电谐振子振动时释放的能量,并假设这些谐振子的能量不能连续变化,而只能取一些分立值,如果振子的固有频率为v则它们只能量最小能量ε0(=hv)的整数倍:ε0,2ε0,3ε0,…,nε0…,这些分立的能量值称为谐振子的能级。后由黑体辐射公式与维恩电热力学得出的普遍公式相比较,即
![]()
与
ρvdv=v3f(v/T)dv
相比较,得出ε0必须与振子的固有频率v成比例。
ε0=hv。
比例常数h称为“普朗克常数”。它的数值是由实验得出的。它是
![]()
表示。
【德布罗意】法国理论物理学家。在量子论的研究中提出了物质波的大胆设想,为此获巴黎大学博士学位,著有“波动力学研究导论”。
【有声电影】当一部电影拍摄时,可见了的景物、人物以及动作被拍摄下来的同时,演员们所说的话及各种声音,通过把声音变成光也被记录在同一胶片上。声音变成光,是用一系列的特殊电子管。首先,声音由微音器收集,把声音变成电脉冲,这与电话中的情况相同。电脉冲在电子管内被放大,然后被送到一个特制的灯泡中去。这种灯泡实际上是一条灯管,它的光的亮度在极短的时间内能作很大的改变,它可以由亮变暗又变亮。这样,声音变成电脉冲,再变成光脉冲。一个响亮的声音产生强光,而一个弱的声音产生暗弱的光。当不同亮度的光照到胶片的声道上,引起不同数目的银原子出现。这和拍照片时发生的现象相同。由于光线的作用,溴化银分子分裂,银原子出现。在胶片被冲洗后,根据原来的声音或强或弱,声道上或明或暗。暗黑的部分,表示响亮的声音。光亮的部分表示微弱的声音,这叫做密度变化式的声道。因为声道从透明变到非常阴暗,即变成非常浓黑。另一种声道是由波纹线组成,这叫做面积变化式声道,因为由波纹线覆盖的面积是变更着的,这两种声道用在电影放映机内,它们的效果相同。光电管是一种特别的电子管。它是有声电影放映机中使声音与影像密切吻合的关键,它的职责是把胶片声道上的声音的照相,或者说声道上光的强弱讯号变成强弱变化的电流讯号,然后再变回声音,虽然光电管并非完成其全部工作,但它负责第一个重要的变换步骤。光电管,包括两个部分——一块弯曲的金属片和一条金属棒,金属片上涂有一层特别的物质,例如铯(电子逸出功很小),以金属片为阴极称为光电阴极,金属棒为阳极,在二电极之间加上一定的电压,当光照在铯上,由于光电效应而放出电子,在电极之间的电场作用下电子从阴极到阳极而形成光电流,当强光照射时,就有较强的电子流流至金属棒;光弱时,电子流较弱,所以光电流的强度是随着光线的亮度而改变的。在电影放映机里,光电管放在胶片声道之前,而光源放在声道之后,于是光线透过声道射入光电管中,在影片不断移动的过程中,通过声道的光的强度也就不断变化,变化的光射向光电管时,在电路中产生变化的电流,把电流放大后,使之通过喇叭可把声音放出来,由于像和声同时制做在同一胶片上,因而,声音和像是同步的。故声和影像的配合完全一致。
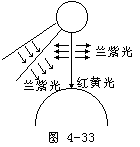
【光的散射】当光通过不均匀媒质悬浮的颗粒或分子时,部分光束将偏离原来方向而分散到各个不同方向去,称之为光的散射。如太阳光束射到地球表面时必须穿过大气层,因此阳光要受到空气分子和悬浮在空中的细小的尘埃粒子的散射。散射光的强度和光波长的四次方成反比,也就是说,波长越短的光,越多地被散射。阳光经过大气层时,其短波部分,如兰光和紫光较多地被散射掉,透过大气层而射到地面上的阳光中波长较长的黄光和红光的成分更多一些。所以没有射向地面而从空中穿过的阳光,它的兰紫色部分被散射到地面。如图4-33所示而使天空呈现蓝色。旭日和夕阳呈红色。这是因为早晚阳光以很大的倾角穿过大气层,经历的大气层要远比中午时厚得多,所以波长较短的蓝光、紫光等几乎全部被散射掉。而剩下波长较长的黄光和红光到达观察者。
【颜色】眼睛对不同波长的光产生的不同的感觉。从而显示出不同的颜色,光的颜色决定于它的频率。一个具有一定波长或频率的光显示出单一的颜色,称为单色光。物体所呈现的颜色由下列诸因素而定:(1)物体本身的性质——光线照射在物体上,物体依照自己的特性有选择地反射或折射某些颜色的光,而其它颜色的光则的被物体吸收,此称为选择吸收。对于不透明物体的颜色是:选择吸收之后剩余反射光的颜色。我们都知道阳光或白炽灯的灯光中包含有红、橙、黄、绿、蓝、绽、紫等颜色。我们称它为“复色光”。如果我们在复色光照明下看物体,譬如红色的布是因为红布反射红色光而吸收其它色光;白色体是将入射的复色白光全部反射。而基本上没有吸收,故显示白色;黑色物体则将入射的复光完全吸收,而无任何色光反射或折出,故呈黑色。而透明体的颜色乃是:选择吸收之后所余的透射光之颜色。如红色玻璃只透过红光而吸收其它的色光,故呈红色。(2)照射光的性质——例如以不含红光之光照射红色物体,即呈现黑色;隔红色玻璃观察不含红光之光源亦呈现黑色。这两种情况都是因为光源中不包含该物体能反射或能透射的光,而其余的色光全被吸收的缘故。(3)入射光透进物体内的深浅——可分双向色性及表面色两个方面。表面色:反射光有一部分自表面立即漫射,另一部分而深入少许而后反射。某种物体对某单色光有较强的反射本领,故在透射之光线中几乎不再有此种色光,但这种物体可能对另一种单色光很少吸收而使它大部分透射过去,于是这种单色光就透过了物体因此就有表面色与透过色互异的现象这就是“双色向性”。如金箔反射黄色光,而透过之光呈蓝绿色;铜箔的透过之光亦为蓝色。追究颜色产生的主要根由,应归结为物质电子能态的改变,不同能态之间的电子跃迁决定了其发光的频率,因而它是产生颜色的根本原因。
【光度学】在光学中研究光的发射、传播、吸收和散射等过程中光的计量问题的学科,也即对可见光的能量计量的学科,研究各种光量,如发光强度、光通量、照度、亮度等的定义及其单位的选定,以及同其他物理量之间的关系,并研究光量测量仪器的设计、制造和测量方法。测量方法可分为目视测量(主观光度学)与仪器测量(客观光度学)两类。光度学的研究对照明的准确计量及设计有重要意义。
【视见率】又称“视见函数”。不同波长的光对人眼的视觉灵敏度。实验表明:正常视力的观察者,对波长5.55×10-7米的黄绿色光最敏感;而对紫外光和红外光,则无视力感觉。取人眼对波长为5.55×10-7米的黄绿光的视见率为最大,取为1;其他波长的可见光的视见率均小于1;红外光和紫外光的视见率为零。某波长的光的视见率与波长为5.5×10-7米的黄绿光视见率的比称为该波长的相对视见率。
【光通量】人眼所能感觉到的辐射能量,它等于单位时间内某一波段的辐射能量和该波段的相对视见率的乘积。由于人眼对不同波长光的相对视见率不同,所以不同波长光的辐射功率相等时,其光通量并不相等。例如,当波长为5.55×10-7米的绿光与波长为6.5×10-6米的红光辐射功率相等时,前者的光通量为后者的10倍。光通量的单位为“流明”。光通量通常用φ来表示,在理论上其功率可用瓦特来度量,但因视觉对此尚与光色有关。所以度量单位采用,依标准光源及正常视力另定之“流明”来度量光通量。
【烛光】发光强度的单位。1967年第十三届国际计量大会统一规定为:在标准大气压下,处在铂凝固温度(2045K)的绝对黑体的1/60000平方米表面上的发光强度为“1烛光”。在此之前,烛光依一标准蜡烛所发的光而定,标准蜡烛是英国所定的烛光,依直径2.2厘米用鲸油制成的蜡烛,每小时燃烧鲸油7.78克。这样标准蜡烛所发的光的强度为烛光。
【发光强度】指光源的明亮程度。也即表示光源在一定方向和范围内发出的可见光辐射强弱的物理量。以光源发射的光通量除以空间的总立体角4π,就是该光源平均发光强度。例如,一点光源沿某一方向的发光强度就是:沿此方向的单位立体角发出的光通量。如果光沿着v方向,取v为轴的一个立体角dΩ,设dΩ内的光通量为dφ,则沿v方向的发光强度为
![]()
发光强度的单位为烛光。
【亮度】表示发光表面的发光强度。发光面在某一方向的发光强度I,除以发光面在该方向的视面积Scosα,就是发光面S在这一方向上
的亮度Ba,如图4-34所示,即
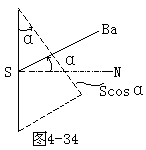
![]()
“或者说,在某方向上从单位表观面积在单位立体角内发出的光通量。亮度一般随观察方向而变,但有某些光源如太阳、黑体、粗糙的发光面,其亮度和方向无关,这类光源叫做朗伯光源。一个理想的漫射面也是沿各方向温射光的发光强度与cosθ成正比,从而光亮度相同,积雪、粉刷的白墙以及十分粗糙白纸的表面,都可近似看成朗伯光源。
【照度】落在受照射物体单位面积上的光通量叫做照度。假设在面
![]()
照度反比于光源到受照射面的距离r的平方,而正比于光束的轴线方向r与受照面的法线n间夹角的余弦,即
![]()
照度的单位为“勒克司”。
【流明】光通量的单位。发光强度为1烛光的点光源,在单位立体角(1球面度)内发出的光通量为“1流明”。
【勒克司】照度的单位。等于1流明的光通量均匀照在1平方米表面上所产生的照度。适宜于阅读和缝纫等的照度约为60勒克司。
【光度计】光度计是对可见光进行计量的仪器,例如,油滴光度计、球光度计等;也有一些光度计可以直接读出光通量、照度或亮度的数值,例如,流明计、勒克司计等。光度计一般都采用与已知发光强度的标准光源作比较来进行测量,例如,油滴光度计、本生光度计;但也有可以直接读出光源的光量,例如,某些流明计。在作比较测量时,可用目视(主观测量)或用仪器(客观测量)两种方法。近年来由于仪器制造技术的提高,仪器测量基本上已替代目视测量。