量的气体分子频繁地碰撞器壁，就对器壁产生持续均匀的压力，气体对器壁的压强就等于器壁单位面积上所受到的这种压力．显然，气体对器壁的压强是大量分子对器壁碰撞所产生的平均效果．因此应着眼于大量分子，用统计方法揭示气体压强这一宏观量的微观实质．

设想有一个边长均为L的正立方体形容器，其中盛有可视为理想气体的某种气体，单个分子的质量为m，分子总数为N．由于大量气体分子做无规则热运动，处于平衡态的气体中这些数目巨大的分子沿各个方向运动的机会是均等的．因此在大量分子的频繁碰撞下，容器中每面器壁上气体对它的压强大小也应是相等的．所以要计算气体压强，只考虑容器的六个面中任何一个器壁面(面积为)所受压力即可．如图所示，建立坐标系．分析与X轴垂直的器壁面所受压力．

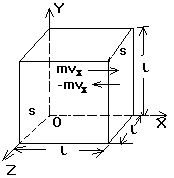
先观察一个速度为v的分子，v在X、Y、Z轴方向上的分量分别为和．一般视分子与器壁的碰撞是完全弹性碰撞，而且仅在碰撞时分子与器壁间才有相互作用．当该分子与面碰撞时，将受到面对它的一个沿－X方向的作用力，致使该分子在X轴方向上的分动量由变为，即X轴方向上分动量的增量为=－2mvx．根据动量定理，面对分子的冲量等于．因此器壁同时受到分子对它的一个等值反向的冲量，冲力方向沿+X轴方向，作用是短暂的．可以设想该分子从面反弹后飞向对面器壁，碰撞后又飞回面发生第二次碰撞．在与面先后两次碰撞间，该分子在X轴方向上通过的距离为2L，所需时间为，即每隔时间该分子碰撞面一次．因此它在单位时间内与面的碰撞次数为．上述仅是一个分子对器壁一个面的作用情况．对于容器有巨大数量的N个分子来说，它们对面接连不断反复的碰撞形成的对面的作用力，完全可视为连续的．该力大小应等于单位时间内全部分子对面的总冲量，即等于单位时间内全部分子跟面碰撞所引起的动量增量总和的负值：

示各个分子速度在X轴上的分量．①由此可得面受到的气体压强为：

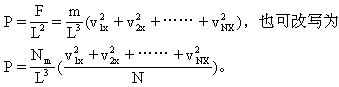
因为对于每个分子来说有

由于处于平衡态的气体，大量分子沿各个方向运动的机会均等，因此可认为

由此，压强的前述关系式可改写为

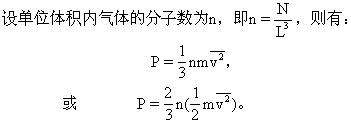
这就是理想气体的压强公式．由式可知，理想气体对器壁的压强与单位体积

    气体压强这一宏观量的微观实质．

要强调说明一点，气体压强是大量分子与器壁碰撞所产生的平均效果，

    都是统计平均量,离开了“大量分子”和“统计平均”来谈气体压强是没有意义的．