①分析题意时,要特别注意对研究对象运动情况的分析,画出草图,并在草图上标明已知量和未知量.如自行车以6米/秒的速度匀速通过汽车站,再前进d=18米后,一辆汽车以3米/![]() 的加速度从汽车站出发追赶自行车.若问汽车在追上自行车之前,何时两车相距最远?解此问题时,要分析清楚两车运动情况的关系.汽车起动后速度由零增大,而自行车速度为恒定值,当汽车的速度小于自行车时,二车间的距离将越来越大.一旦汽车的速度增长到超过自行车速度时,两车距离才逐渐变小,可见两车速度相等时,两车相距最远.作位移草图如图所示,设汽车经
的加速度从汽车站出发追赶自行车.若问汽车在追上自行车之前,何时两车相距最远?解此问题时,要分析清楚两车运动情况的关系.汽车起动后速度由零增大,而自行车速度为恒定值,当汽车的速度小于自行车时,二车间的距离将越来越大.一旦汽车的速度增长到超过自行车速度时,两车距离才逐渐变小,可见两车速度相等时,两车相距最远.作位移草图如图所示,设汽车经![]() 秒速度增长到6米/秒.由公式v=at或得
秒速度增长到6米/秒.由公式v=at或得
![]()
这时两车相距最远其大小为
![]()
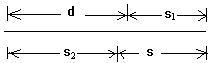
②解题时,要选择恰当的公式,建立解题方程,在方程中尽量不要包含那些与已知量、未知量都无关的量,这样使解题将简便得多.如一物体做匀变速直线运动,从A到B,已知![]() ,及A、B之间距离为s.若求物
,及A、B之间距离为s.若求物
![]()
③匀变速直线运动的基本公式是矢量方程,其中![]() 都是在一条直线上的矢量,它们只有两种可能方向,所以解题时可规定一个正方向后,用正负号来表示已知量的方向,求解出的未知量为正,则表示其方向与所确定的正方向一致,反之相反.
都是在一条直线上的矢量,它们只有两种可能方向,所以解题时可规定一个正方向后,用正负号来表示已知量的方向,求解出的未知量为正,则表示其方向与所确定的正方向一致,反之相反.