与绳的受力特点不同，由于杆既能发生纵向的拉伸或压缩形变，又能发生横向形变，所以杆对物体的作用既可以是沿杆方向的拉力或推力，也可以是在其它任意方向上的弹力．如果把杆视为刚体，则杆的弹力可以发生突变．杆对物体的作用力往往需要根据杆或连接在杆上的物体所受到的其他力的情况及运动状态来确定．

    杆的运动既可以是平动，又可以是转动，在共面力系作用下，杆处于平衡状态的充分必要条件为∑F=0，在正交坐标中也可以写作

    

    ∑M=0或

    

    如果处于平衡的杆所受的各外力是共点力，由于各力对各力作用线交点的力臂为零，则杆的平衡条件只由①式决定．当杆有一个固定转动轴时，杆就不能平动，这时杆的平衡条件就只由②式来决定．

    对杆件的受力分析，在中学阶段通常只研究“二力杆件”和“三力杆件”两种情况．

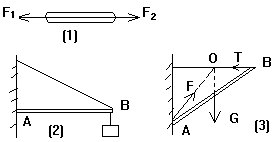
    若一个杆件只受两个外力的作用而处于平衡，我们把这样的杆件称为“二力杆件”如图(1)所示．由物体的平衡条件可以知道力和大小相等、方向相反，并用两个力的作用线一定和杆件的轴线重合，又如图(2)所示，可忽略重力的轻杆AB处于平衡态，由于只在A和B两端受到力的作用，所以属于“二力杆件”，即在B端两个绳的弹力之合力一定沿杆向左，而墙对A端的压力一定沿杆向右，这两个力是一对平衡力．

    如果杆件只受互相不平行的三个外力作用处于平衡，我们称之为“三力杆件”平衡．根据三力平衡原理，这三个力一定汇交于一点，如图(3)，均匀重杆AB属于“三力杆件”，杆的重力G作用线和拉力T的作用线交点为O，可以判断出墙对杆的A端的压力F的方向一定通过O点．

    三力平衡在静力学中是很普遍的，因此对“三力杆件”特点的认识和对其受力分析的研究是十分重要的．