图(1)中，质量为m的小球在光滑的倒锥形桶壁上做匀速圆周运动，它所需的向心力就是重力G与桶壁支持力N的合力．该合力的方向指向圆心O'(不要误认为是O)，若桶壁与竖直方向的夹角为q，则向心力为

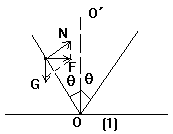
    由上式知，当小球速率增大时，做圆周运动的半径随之增大，小球将沿桶壁上升．

    向心力公式把做圆周运动质点的运动情况与受力情况联系了起来，如果知道受力情况当然可以确定运动情况；反之，如果知道运动情况也可确定受力情况，如，在图(2)中，一粗糙水平圆盘可绕过中心轴OO'旋转，现将轻质弹簧的一端固定在圆盘中心，另一端系住一个质量为m的物块A，设弹簧劲度系数为k，弹簧原长为l．将物块置于离圆心R处，R>l，圆盘不动，物块保持静止．现使圆盘从静止开始转动，并使转速w逐渐增大，物块A相对

    擦力，如果受到静摩擦力，试确定其方向．

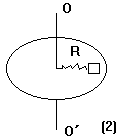
    对物块A，设其所受静摩擦力为零时的临界角度为，此时向心力仅为弹簧弹力；若，则需要较大的向心力，故需添加指向圆心的静摩擦力；若，则需要较小的向心力，物体受到的静摩擦力必背离圆心．

    依据向心力公式，有

    

    

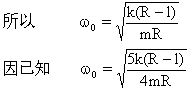
    得

    可见物块A所受静摩擦力指向圆心．

    从此题可以看出，圆周运动问题仍然是物理基本定律(如牛顿定律)的运用问题，受力分析仍然是解题的关键．