简谐运动的位移公式为我们可以在直角坐标系中作出描述作简谐运动的振子的位移随时间变化的函数关系图象．如图所示．图中坐标轴横轴表示平衡位置，横轴的长度表示时间．振动图线上某点在纵轴上的射影是振子相对平衡位置的位移．

    简谐运动的位移－时间图象记录了某振子在一段时间内全部振动的过程中每一时刻所对应的位移．反映出在振动过程中速度、加速度的变化规律，使我们对简谐运动的运动规律有一个定性的了解．

    应用简谐运动的位移－时间图象可以从已知的时刻判断振子的位移的大小和方向、速度的方向以及加速度的方向．

    例如：在图中，弹簧振子的振动周期是2s，振幅是5cm，角频率为

    t=1s处作t轴的垂线，交位移－时间图线于C点，过C点作t轴的平行线，交于纵轴一点，该点坐标即为我们要求的位移大小和方向，振子的位移为+5cm．又如求振子到达位移是+2.5cm的时刻的方法是先过纵轴+2.5cm点作时间轴的平行线，交振动图线于A、B点两点．A、B两点所对应的时刻即为振子到达+2.5cm处的时刻．

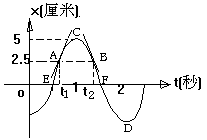
    我们可以从图线的切线的斜率判断振子的速度方向．在A点图线的斜率为正，则振子在该时刻的速度方向与我们规定的正方向相同．反之，在B点图线切线的斜率为负，振子此时刻的速度方向与我们规定的正方向相反．进一步可以知道振子在C、D两点的速度为零．E、F点的速度最大．

    

    时刻振子的加速度都是指向平衡位置．再根据振子的速度方向可知，时刻振子作减速运动，时刻振子作加速运动．