这种问题中常有与物体平衡等力学知识相联系的内容.解题时,一要根据题目要求选择好研究对象;二要结合寻求气体压强的需要,进行相关物体的受力分析.
例:如图所示,一个上下都与大气相通的直圆筒,内部横截面的面积![]() ,中间用两个活塞A与B封住一定质量的理想气体,A、B都可沿圆筒无摩擦地上、下滑动,但不漏气,A的质量可不计.B的质量为M,并与一劲度系数
,中间用两个活塞A与B封住一定质量的理想气体,A、B都可沿圆筒无摩擦地上、下滑动,但不漏气,A的质量可不计.B的质量为M,并与一劲度系数![]() 的较长的弹簧相连.已知大气压强
的较长的弹簧相连.已知大气压强![]() ,平衡时两活塞间的距离
,平衡时两活塞间的距离![]() .现用力压A,使之缓慢向下移动一定距离后,保持平衡.此时,用于压A的力
.现用力压A,使之缓慢向下移动一定距离后,保持平衡.此时,用于压A的力![]() .求活塞A向下移的距离(假定气体温度保持不变.)
.求活塞A向下移的距离(假定气体温度保持不变.)
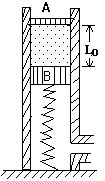
解题思路:题中将气体的状态变化及气体、活塞、弹簧等的相互作用和受力平衡问题相互渗透结合在一起.涉及到的物体有A、B两个活塞、被封闭的气体以及弹簧等.它们在发生题设的变化前后都分别处于平衡状态.即使是在向下压A的缓慢变化的过程中,也可把气体的经历视为平衡过程,活塞和弹簧也分别经历一系列平衡状态.首先选定被封闭的气体为研究对象.但同时还应看到,被封闭气体的等温压缩、活塞B在平衡状态的受力变化以及弹簧在外界压力作用下的形变导至弹力发生变化等这几个物理过程都是被它们之间力的相互作用这条主线贯穿在一起的.为了循这条主线抓住其间的内在联系,在解题中还要根据需要适时地变换研究对象~如始终处于平衡状态的活塞B及形变中的弹簧等,进行必要的受力分析,建立与被封闭气体力的作用关系,理顺思路,即可逐一解决.
解:设被封闭气体在等温压缩过程,活塞A向下移动距离为L,活塞B向下移动距离为x,根据玻意耳定律有
![]()
由于在这个过程中,弹簧增加的压缩量也就是B向下移动的距离x,弹簧对B增加的弹力也就等于F,因此根据胡克定律有
F=kx.
将上面两式联立,消去x,代入数据,即可得活塞A向下移动的距离L=0.3m.