体在宏观上处于平衡态时，虽然单个分子的速率都不相同，并且由于相互碰撞而不断发生变化，但平均说来，速率在某一范围内的分子数占有总分子数的百分比总是一定的，这个比值只与气体的种类及温度有关．英国物理学家麦克斯韦于1859年应用统计概念首先导出：气体处于平衡时，气体分子的数目按速率分布的规律．

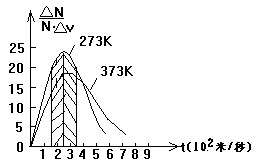
按照麦克斯韦的分子速率分布函数，对氧气在0℃和100℃时分子速率的分布情况画出分布函数曲线，如图所示．

从图中可看到,在0℃时速率在300~400m/s这一速率区间的分子数最多，占有总分子数的21.4％；速率大于400m/s和小于300m/s的分子数依次递减，速率很大的(900m/s以上的只占有0.9％)和很小的(100m/s以下的只占1.4％)分子都很少．形成“中间多，两头少”的统计分布规律．温度升高到100℃时，虽然这种分布规律不变，但与分子数所占比例最大值(18.6%)相对应的速率区间却移向速率大的一方，出现在400~500m/s区间．这说明，温度升高时，速率小的分子数减少(如100m/s以下的由1.1%降为0.7%)，而速率大的分子数增多(如900m/s以上的由0.9%增为3.9%)．显然，这种分子速率的分布规律是一种统计规律．上述的各速率区间的相对

    种类固定不变，在同一温度下就会有确定的分子速率分布．

既然在一定温度下，某种气体的分子速率分布是确定的，就可以求出在这个温度下这种气体分子的平均速率，即所有分子的速率的平均值．从麦克

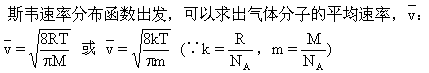
或中R是摩尔气体恒量，M是某种气体的摩尔质量；k是玻尔兹曼常数，

    于温度升高时，速率大的分子数增加，因而分子的平均速率增大．