物体以一定初速度沿竖直方向，向上抛出后，只受重力作用下的运动．

    竖直上抛运动可分为两个阶段来研究，一个是上升过程，这时它的初速度和重力加速度g方向相反，是匀减速直线运动．上升到最高位置时，末速度为零，但加速度仍为g，因此从这一时刻(最高位置)开始，它又将作自由落体运动(称为下落过程)．

    由于物体在上升和下降过程中，加速度都是g，即加速度的大小和方向都是恒定不变的，所以又可以把竖直上抛运动看做一个统一的匀变速运动来

    计算，s为正，表示物体在原抛出点上方，如为负时表示物体已下落到原抛出点的下方．同样，用公式计算出的末速度，当时，表示物体向上运动，时表示物体正在向下运动．

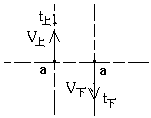
    研究竖直上抛运动时，要注意其对称性特点：某一段上升所用的时间和同一段下落的时间相等．物体上升时经过某一高度时的即时速度大小与下落时经过该同一高度的即时速度大小相等(方向相反)．如图所示，我们把竖直上抛看成一整体来证明这个结论：物体由a点上升后，又回到a点时是位移s=0．

    

    所以

    负号表示物体在a点的两个速度方向相反．

    上升时间可由公式求出：

    

    

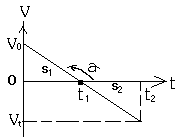
    竖直上抛运动的v－t图象如上图所示，三角形面积为上升阶段的位移，取正值．三角形面积为下落时的位移，取负值．如果物体回到抛出点，则合位移为零，即．由图线可以看出：上升时间等于下落时间；抛出的初速度值和下落到抛出点的速度值相等．

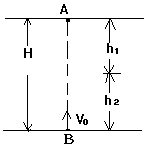
    解竖直上抛习题时，正方向的建立虽有任意性，但也要注意正负号问题容易出现错误．如，物体A从80米高处自由下落，与此同时，在它正下方的地面上以40米/秒的初速度竖直向上抛出物体B．试分析二者经过多长时间在何处相遇？我们可以画出如图所示的位移关系图，设A下落了，B上升了，为了保证中和都是正值，我们规定正方向时，对于A应取向下为正，而对于B应取向上为正．

    

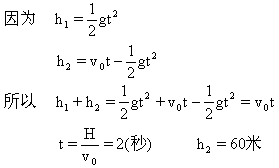
    即二者经历2秒相遇．当然在解此题前还要判断一下，两物体能否在空中相遇．通过分析计算可知，A和B在空间运行时间都是4秒，因此B在上升到最高点以前便能与A相遇．

    如果以A为参照物，则因A、B的加速度大小和方向相同，所以B对A的相对加速度为零，则B以对A作匀速直线运动，那么B和A相遇时：

    

    

    可见选择合适的参照物，能使解题大为简化．