(一)运动合成分解法.
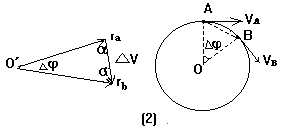
图(1)中,设质点以速率v沿顺时针方向做圆周运动,圆周半径为r,当从A运动到B时,弦AB所表示的位移可看成切向位移AC和法向位移CB的矢量和.切线方向质点做匀速直线运动,法线方向可视为做初速度为零的匀加速直线运动,其加速度设为a.
由几何关系知
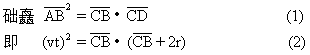
当Dt→0时,有
![]()
(2)式变为
![]()
由(3)式得
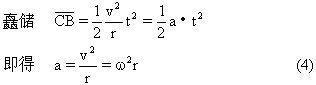
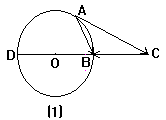
(二)极限法.图(2)中,做匀速圆周运动的质点在A点时即时速度为![]() ,在B点时即时速度为
,在B点时即时速度为![]() ,二者大小相等.将
,二者大小相等.将![]() 两速度矢量平移于一起
两速度矢量平移于一起
![]()
当Dt→0时,Dj→0,a→90°,Dv的极限方向垂直![]() 并指向圆心.
并指向圆心.
比较矢量三角形及△ABO,由相似关系知
![]()
由(2)式得
![]()
用Dt除(3)式两端,得
![]()
![]()
故有
![]()