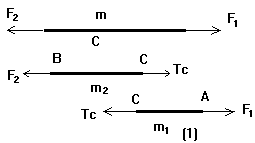
有外力作用于绳子使绳伸长时,绳子内部之间产生弹力,这种弹力的特点是只有当绳子伸长时才存在,因此称此种弹力为张力.设绳子AB两端作用拉力![]() ,C为绳上任一点(如图(1)).我们可以把绳看作是由AC和BC两部分组成,显然AC和BC两部分之间有张力作用,设此张力为
,C为绳上任一点(如图(1)).我们可以把绳看作是由AC和BC两部分组成,显然AC和BC两部分之间有张力作用,设此张力为![]() .
.
在物理教学中,考虑到绳的实际情况和研究问题所允许的近似,常把绳作为两种理想化模型来处理.
一种情况是,绳是轻绳,其质量极小,与问题中其他物体相比质量可以略去.如图(1)中,设![]() ,当绳运动稳定后即不再伸长时,根据牛顿第二定律
,当绳运动稳定后即不再伸长时,根据牛顿第二定律
对m有 ![]()
①
![]()
②
如果,m=0则有![]() .这就是说,在力学问题中,只要存在绳子质量可以略去的条件,对于只在两端受力的绳来说,尽管加速度不为零,则这两个力一定相等,而且绳子的张力也处处相等,此张力等于绳子所受的外力.如图(2)所示,一光滑定滑轮通过细绳挂两个质量
.这就是说,在力学问题中,只要存在绳子质量可以略去的条件,对于只在两端受力的绳来说,尽管加速度不为零,则这两个力一定相等,而且绳子的张力也处处相等,此张力等于绳子所受的外力.如图(2)所示,一光滑定滑轮通过细绳挂两个质量![]() 的物体.求绳子的张力和物体系的加速度?
的物体.求绳子的张力和物体系的加速度?
依题意绳的质量可以忽略不计,所以绳子两端受到的力大小相等,它们分别是![]() 的反作用力,由牛顿第二定律(设
的反作用力,由牛顿第二定律(设![]() )
)
![]()
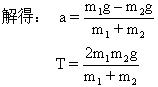
代入数据后![]() T=48牛顿
T=48牛顿
由上面各式可知,绳子受力(T的反作用力)的大小由系统其他力决定(此处为重力);只有当系统处于平衡状态时(a=0),![]()
由①②式,还可看出,当质量不为零而加速度为零时,![]() 也等于
也等于![]() ,并且绳子中各点张力也都等于
,并且绳子中各点张力也都等于![]() ).在静力学中,力能传递就是基于这个道理.如图(3)所示,在水平力F的作用下,系统保持静止状态,则各物体左右所受到的水平力大小都是F,“好像”力F能够传递.这实质上是由于加速度等于零的结果.若加速度不为零,水平方向的力就一定不相等了.
).在静力学中,力能传递就是基于这个道理.如图(3)所示,在水平力F的作用下,系统保持静止状态,则各物体左右所受到的水平力大小都是F,“好像”力F能够传递.这实质上是由于加速度等于零的结果.若加速度不为零,水平方向的力就一定不相等了.
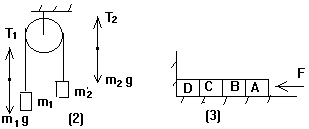
第二种理想情况是假定绳子是刚性的,刚性绳是指绳子的劲度系数k非常大,它只要有极微小的形变就可以产生足够大的弹力.因此刚性绳中的弹力可以在Dt→0的时间内,能够产生突然变化(而弹簧中的弹力要发生变化,就需要有明显的形变,需要明显的不可忽略的时间,即弹簧的弹力不能够产生突变).如图(4)所示,质量m的小球,通过细绳OB和OA系着处于平衡,现突然将AO剪断,在剪断瞬间,OB线上的张力为多少?题中,若绳子的质量比小球质量m小的多,可以忽略.剪断前,小球受力情况如图(5)所示,

果假设绳子是刚性的,那么绳上的张力则由系统中其他力和运动状态决定,由于剪断OA后,小球的运动状态要变化,因而绳OB受力就要变化.在无限小时间内,小球从静止状态转化为摆动状态,因而受力情况如图(6)所示,由牛顿第二定律

当Dt→0时,v→0
所以 T=mgcosa
可见,把绳子看成是刚性的或非刚性的模型,在剪断OA瞬间它受力的大小是不同的.