据有固定转动轴物体的平衡条件为原理制成的称量物体质量的工具．如图(1)所示．O处是提纽，为杆秤的固定转动轴；B处固定秤钩，用以吊挂被测重物；C点为杆秤的重心；当秤钩上没有挂被称物体时，移动秤锤于A处提起提纽，使秤杆平衡，则秤锤的位置A点就是杆秤的零刻度，也叫做定盘星．

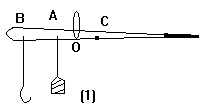
    把质量为50g(1市两)的物体挂在秤钩上，调整秤锤的位置，使杆秤平衡，这时秤锤的位置就是秤的50g的刻度．再把秤钩上挂的质量换为100g、200g等物体，使杆秤平衡就能找出100g、200g等刻度的位置等等．一旦杆秤上刻度确定后，提纽、挂钩的位置和秤锤的质量就不能再改变，否则原刻度线就得重新修定．

    实用中的杆秤，定盘星也可以在提纽的右侧，但此杆秤的重心在左侧，总之定盘星和杆秤的重心，一定在提纽的两侧．

    杆秤问题的计算，实质上是有固定转动轴物体平衡条件的应用，如我们证明杆秤的刻度是均匀的，即称重物时，秤锤的位置到定盘星A点的距离和被称重物的质量成正比时，可列出两个方程，其一为不挂重物时的力矩平衡方程，另一个是挂上重物后的力矩平衡方程，就可求解．即不称重物时(图(1)所示)：

    其中为杆的质量，为秤锤的质量．

    秤钩上挂上重物mg后：

    

    由①②式得：

    

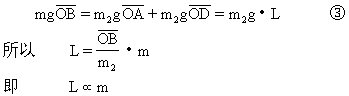
    市场上所谓不准秤，是不法商人将杆秤的秤锤换成小质量的，由③式可知，在同一刻线上(L一定)只需要较小的质量m，就能使杆秤平衡，这样消费者利益就受到损害．或者加大秤钩(盘)的重力，或者将杆秤内部掏空，并在其中注入流动性好的水银，称重时，抬高秤尾，使水银流到有挂钩(盘)的一端，这样③式就成为

    

    其中m'表示水银或秤钩(盘)所增加的质量，可以看到，当、L一定时，所要称的质量m自然减小．