地球及其它行星的公转轨道近似于圆，行星的运动可看成以太阳为中心的匀速圆周运动．设想行星做圆周运动的向心力就是太阳对行星的吸引力，若行星质量为m，公转周期为T，轨道半径为r，由牛顿第二定律可得

    此式说明太阳对行星的引力与它们间的距离平方成反比，与该行星的质量成正比，式中的m，各个行星都相等，它是一个与行星无关，只与太阳性质有关的常量．

    进一步研究发现，卫星绕行星的运动也遵从同样的规律，这时，(3)式中的m为卫星的质量，r是卫星的轨道半径，m则是仅由该行星决定的常量．这说明，太阳对行星(如地球)的作用力与行星对卫星(如地球对月球)的作用力属同一性质的力．

    牛顿设想地球作用于地面上物体的重力也是这一性质的力．他巧妙地把地面上的重力推广到月球轨道上．月球绕地球的运动可以似看成匀速圆周运动，设月球运转周期为，月地距离为R，则月球的向心加速度为

    若重力也遵从平方反比规律，则月球轨道处的重力加速度与地面重力加速度g的比值为

    牛顿时代人们已测知≈60R．地球半径公里，T≈2.36×秒．将这些数据代入(4)、(5)两式，可得

    这说明，地球对地面物体及月球的作用力均遵从平方反比规律，牛顿设想，地球对太阳的作用力也应如此，即

    式中，M为太阳质量，m'是仅由地球决定的常量．比较(3)、(6)两式，并运用牛顿第三定律，可知

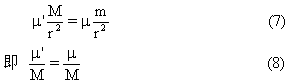
    (8)式说明该比值是一个与地球及太阳质量均无关的常量，设该比值为G，则有m=GM．将m=GM代入(3)式，可得

    由于太阳对行星、行星对卫星、地球对地面物体的作用力都遵从(9)式所表达的规律，牛顿将它做了合理推广，即任何两个物体间都存在相互作用的吸引力，力的方向沿两物体的联线方向，力的大小与两物体质量的乘积成正比，与两物体之间的距离的平方成反比，其数学表达式仍如(9)式所示．