在长为L的细绳下端拴一个质量为m的小物体，绳子上端固定，设法使小物体在水平圆周上以大小恒定的速度旋转，细绳就掠过圆锥表面，这就是圆锥摆，如图所示．

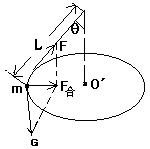
    从图可知，小球做圆周运动的圆心是O'，做圆周运动的半径是Lsinq，小球所需的向心力实际是绳子拉力F与重力G的合力．并有

    

    由此式可

    

    这说明做圆锥运动的小球的摆线与竖直方向的夹角与摆球质量无关关，与摆线长度及角速度有关．当摆长一定时，角速度越大，q越大．由于绳子拉力

    可见绳子拉力随角速度的增加而增大。小球旋转一周所经历的时间若用T表示，则从该式及中消去ω可得

    该式称为圆锥摆的周期公式．在地球表面同一地点，圆锥摆的周期与成正比，而与小球质量无关．若摆线L为定长，则ω越大，θ越大，周期越小．