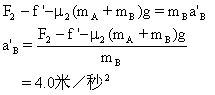顿运动定律是经典力学的基础定律.它以牛顿第二定律为核心,解决了运动和力的关系问题.
由牛顿第二定律公式∑F=ma可知,式中m表示研究对象的质量;等式左边∑F表示物体所受到的外力的合力.等式右边a表示物体在∑F作用下的瞬时效果,∑F是“因”,a是“果”;等号表示等式左右两边不仅数值大小相等,而且∑F与a方向一致,∑F=ma是矢量等式.
运用牛顿第二定律解题的基本思路是:
1.仔细审题,明确研究对象;
2.隔离研究对象,进行受力分析,画好受力图;进行运动分析,画好运动草图;
3.建立适当的坐标系,进行力的正交分解,根据牛顿第二定律建立动力学方程![]() 根据运动学公式建立运动学方程;
根据运动学公式建立运动学方程;
4.求解方程组,对结果作必要的讨论和说明.
如图所示.木块A、B叠放于水平面上,它们的质量分别为![]() =4.0千克,
=4.0千克,![]() =6.0千克.A、B间的动摩擦因数
=6.0千克.A、B间的动摩擦因数![]() =0.25.其相互作用的静摩擦力的最大值为
=0.25.其相互作用的静摩擦力的最大值为![]() =12牛,B与水平面间的动摩擦因数
=12牛,B与水平面间的动摩擦因数![]() =0.20.现用水平恒力F向右拉B,在下述两种情况下,两木块的加速度及二者间的摩擦力各是多少?
=0.20.现用水平恒力F向右拉B,在下述两种情况下,两木块的加速度及二者间的摩擦力各是多少?
(1)F=40牛
(2)F=54牛.(计算中取g=10米/![]() )
)
解:先求出A、B能保持相对静止的最大加速度![]() ,由
,由![]() 可知:
可知:
![]()
设此情况下作用于B的水平拉力为![]() ,以整体为研究对象,根据牛顿第二定律有:
,以整体为研究对象,根据牛顿第二定律有:
![]()
所以 ![]()
=50牛
当![]() 时,A、B相对静止;
时,A、B相对静止;
当![]() 时,A、B间有相对滑动.
时,A、B间有相对滑动.
(1)![]() ,A、B相对静止,加速度
,A、B相对静止,加速度![]() ,由①式可得:
,由①式可得:
![]()
![]()
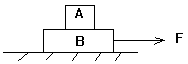
(2)![]() ,A、B相对滑动.此时A受到B给它的水平向右的滑动摩擦力f'的作用,依滑动摩擦力公式有
,A、B相对滑动.此时A受到B给它的水平向右的滑动摩擦力f'的作用,依滑动摩擦力公式有![]() ;根据牛顿第二定律可知:
;根据牛顿第二定律可知:
![]()
根据牛顿第三定律可知,A对B的滑动摩擦力水平向左,大小也是10牛.以B为研究对象,根据牛顿第二定律: