§ 3 Integrals of functions of complex variables 

 

First, the definition and formula of the integral of the complex variable function

 

    Let be an oriented curve in the complex plane

                    

The positive direction of is along the direction of parameter increase , and the curve in the opposite direction is denoted as . For any arbitrary

                   

there is a corresponding

                

They divide the curve into segment arcs . If the single value is continuous on the curve , then when

                       

Japanese

                         

When there is a limit of , the limit is called the integral of the function along the curve , denoted as

                           

If it is a piecewise smooth curve * , which is a piecewise continuous and bounded function on , then the function must be integrable along the curve .

    The integral of the complex variable function along the curve can actually be transformed into the curve integral of two two-variable real variable functions, so their integral formulas have many similarities (in the following formulas, the integrand functions are assumed to be on a piece-by-piece smooth curve . Single value continuous):

                        ( is a complex constant)

              

                

                                   ( It is made of curves and connections)

              

    Set on the curve , the length of the curve is , then

               

 

Second, the properties of the integral of the analytic function

 

    [ Cauchy's integral theorem ]   The Cauchy integral theorem has the following forms:

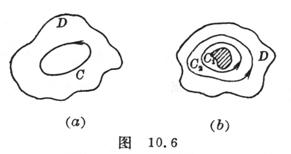
    1 ^o If the function is analytic in a simply connected region , then the integral along any simple closed curve ** in it ( Fig. 10.6 ( a )) is equal to zero, i.e. 

             

    2 ^o If the function is resolved in a multi-connected region and is any two closed curves around the same hole (Fig. 10.6 ( b )), then 

              

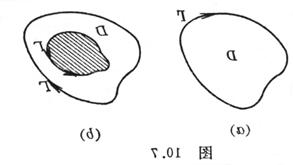
    3 ^o If the function is resolved in a simply connected region , continuous over the package * of , then the integral along the region boundary is equal to zero (Fig. 10.7 ( a )), i.e. 

               

    4 ^o If the function is analytic in a multi-connected region , continuous in the upper region, then the integral along the region boundary (Fig. 10.7 ( b )) is equal to zero, i.e. 

                

    [ Indefinite integral ] A function whose   derivative is equal to is called an indefinite integral (original function) .

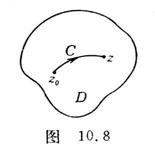
    According to Cauchy's theorem, the integral of an analytic function in a simply connected region along any piece-wise smooth curve in the region is only related to the two endpoints of the curve and has nothing to do with the route of the integral (Figure 10.8 ), so it can be written as

                

    Let be any indefinite integral, then

                

    [ Cauchy integral formula ]   If the function is analyzed in the region D enclosed by a simple closed curve , and is continuous on the above, then for any point in _D , we have

                        ( take the positive direction)

This formula shows that the value of the analytic function at any point in the region can be determined by the value on the boundary, and it also shows that the value of the analytic function in the region has a close relationship with the boundary value, which is of great significance in application ( Figure 10.9 ( a )) .

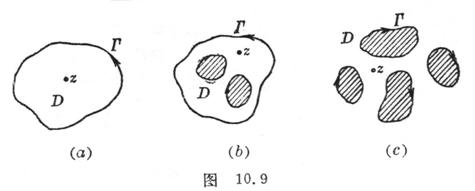
The Cauchy integral formula also holds for the multi-connected region enclosed by finite simple closed curves (Fig. 10.9 ( b )) .

    The Cauchy integral formula also holds for unbounded regions (Fig. 10.9 ( c )): if the bounds of the unbounded region (inclusive ) are finite simple closed curves , the function is analytic except for points inside and continuous and exist at the same time, then for any point within

                   

                                                   the direction is to make the left side of it )

    [ Cauchy-type integral ] Suppose a closed or non-closed piecewise smooth curve is a continuous function on , then for any point not on , the integral

                      

is a single-valued function, called the Cauchy integral of , denoted as _.

    The Cauchy-type integral is analytic in any simply connected region of points that do not contain a curve , and its higher-order derivative is

                 

 

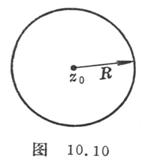
    [ Average Theorem ] If the function is analyzed in a circle with a center and a radius , and is continuous on the circle, then the value of the function at the center of the circle is equal to the arithmetic mean of the values ​​on the circumference, that is,

                 

    [ Maximum Modulus Theorem ]   If the function is analytic in a bounded region , continuous on , and the maximum value set on is , then there is a point on the boundary of , such that for all the

               

    [ Higher-Order Derivative Theorem ] If the function is analytic in the region and continuous in the upper region, then there are derivatives of various orders at every point within it, and there are

                 ( yes border)

    This theorem shows that as long as it exists, then the higher-order derivative also exists, which is a property that the real variable function generally does not have .

    [ Cauchy's inequality ] If the function is analyzed in the area , continuous on the upper, and the shortest distance from the point to the boundary is , and the length is , then

            

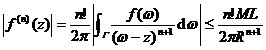
In particular, when it is a circle , there are inequalities

               

   [ Liuville's Theorem ] If a function is analytic and bounded in the full plane, then it must be equal to a constant .

   [ Morella's Theorem ] If a function is continuous in a simply connected region , and the integral along any simple closed curve in it is equal to zero, then it is analytic in the region .

   [ Poisson Formula of Harmonic Function ] Suppose it is harmonic in a circle , continuous on a closed circle , and is any point in the circle, then

              

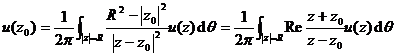
In polar coordinates, there are forms: