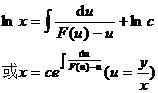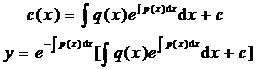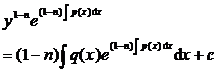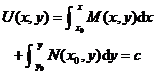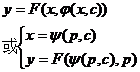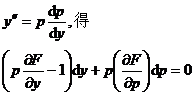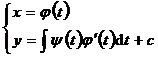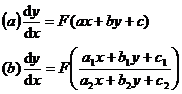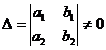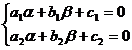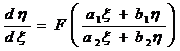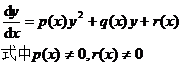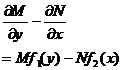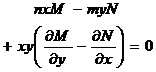§ 2 First-order differential equations
1. Existence and Uniqueness of Solutions to First-Order Differential Equations
The general form of a first-order differential equation is
![]()
If on the region under consideration , then according to the existence theorem of implicit functions (Chapter V
§ 3 , 4, 2 ), the solution yields![]()
![]()
![]()
or written in symmetrical form
![]()
[ Theorem of Existence and Uniqueness of Solutions ]
Given a Differential Equation
![]()
and initial value .![]()
Set in closed area :![]()
![]()
![]()
is continuous, then there is at least one solution to the equation, which takes value at and is deterministic and continuous in a certain interval included (this theorem is called Cauchy's existence theorem) .![]()
![]()
![]()
![]()
If the inner pair variable also satisfies the Lipschitz condition, that is, there is a positive number , such that for any two-valued sum of the inner pair , the following inequality holds:![]()
![]()
![]()
![]()
![]()
![]()
![]()
Then this solution is unique .
Two, integrable types and their general solutions
( C is an arbitrary constant in the table)
|
Equation Type |
Solution points and general solution expressions |
|
1 . Variable Separation Equations
f 1 ( x ) g 1 ( y )d x +
f 2 ( x ) g 2 ( y )d y =0 |
Separate the variables, divide both sides by g 1 ( y ) f 2 ( x ) , and integrate separately . |
|
2. Homogeneous equations
General assumptions then the variable is separable and belongs to type 1 |
make Substitute into the original equation to get the equation of the new unknown function u about the independent variable x :
x d u = [ F ( u ) – u ]d x Then solve for type 1 .
|
|
3 . Linear equation Equation Type |
First find the corresponding homogeneous linear equation
Solution points and general solution expressions |
|
When q ( x ) ≡ 0 , it is called a homogeneous linear equation, and when , it is called an inhomogeneous linear equation |
general solution Reusing the method of constant variation ( § 3, 2 , 2 of this chapter ), let
Calculate and substitute into the original inhomogeneous linear equation , we can get
|
|
4 . Bernoulli equation
|
Use variable substitution to transform the original equation into a linear equation about the new unknown function , and then solve it according to type 3 .
|
|
5 . Full (proper) differential equations M ( x , y )d x + N ( x , y )d y =0 where M and N satisfy
|
The equation can be written as M ( x , y )d x + N ( x,y )d y =d U ( x,y )=0 where d U is the total (proper) differential .
|
|
6 . Equations that can be solved for y y = F ( x,p ) in the formula |
Taking the derivative of both sides of the equation with respect to x , we get
or
If the general solution of this equation can be found or , then the original equation can be solved .
|
|
[ Lagrange equations ] y = xf 1 ( p ) + f 2 ( p ) where is a known differentiable function [ Clero Equation ] y = xp + F ( p ) where is a known differentiable function Equation Type |
A linear equation that can be reduced to x
Then solve according to type 3 turn into an equation
Let , that is, p = c , and substitute it into the original equation . Solution points and general solution expressions |
|
|
( see § 2, 3 ) |
|
7. Equations that can be solved for x x = F(y, p) in the formula |
Taking the derivative of both sides of the equation with respect to x , use
If the general solution of this equation can be found Then the original equation can be solved .
|
|
8. Equations without explicit unknown functions |
By introducing the appropriate parameter t , the original equation is transformed into
|
|
|
Introducing the parameter t , the original equation is
|
|
10 . Equations that can be reduced to separable or homogeneous equations
Equation Type |
( a ) Let z = ax + by + c , convert the original equation to type 1
( b ) If the determinant
Introduce new variables
where α and β satisfy the equations Solution points and general solution expressions |
|
|
Then the original equation is transformed into a homogeneous equation ( type 2):
If =0, b 1 ≠ 0 , then let z = a 1 x + b 1
y + c 1 ; If =0, b 2 ≠ 0, then let z = a 2 x + b 2 y + c 2, So the original equation is reduced to type 1. |
|
11. The Riccati equation
|
If it is known that the original equation has a particular solution y=y 1 ( x ) , make the transformation
The original equation can be transformed into a linear equation ( type 3) :
Or use the transformation y = y 1 ( x ) + u to convert to Bernoulli's equation ( type 4):
Then solve according to type 3 and type 4 respectively . |
|
12.
Equations with integral factors M ( x, y ) d x + N ( x, y ) d y = 0 in the formula
But there exists μ ( x, y ) that satisfies
μ ( x, y ) is called the integral factor of the original equation |
Find the integral factor μ ( x, y ), and then solve it according to type 5. The method of finding the integral factor is shown in the table below . |
How to find the integral factor
|
condition |
Integration factor μ ( x, y ) |
condition |
Integration factor μ ( x, y ) |
|
xM+yN =0
xM+yN ≠ 0 condition |
Integration factor μ ( x, y ) |
condition |
of the form m ( x ) n ( y ) Integration factor μ ( x, y ) |
|
M,N are homogeneous forms of the same degree
M(x, y) = yM 1
(xy) N(x, y) = xN 1 (xy)
|
|
there is suitable
That is, M+iN is an analytic function of x+iy in the simply connected region that satisfies the differential equation |
x m y n |
3. Strange solutions and their solutions
[ Singular solution of differential equation ]
The envelope of a family of integral curves (general solutions) of a differential equation is called the singular solution of this differential equation . A singular solution is the solution of the equation, and there is more than one integral curve passing through each point on the singular solution. , that is, at every point on the singular solution, the solution of the equation is not unique .![]()
[ c - discriminant curve method ] Let the general solution of the first-order differential equation be , where c is an arbitrary constant, and c is regarded as a parameter . From the following equations![]()
![]()
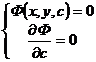
All the curves obtained by eliminating c are called the c - discriminant curve of the curve family, which contains the envelope of the curve family . However, it should be noted that the c - discriminant curve is not necessarily the envelope of the curve family. Check .![]()
![]()
Example to find a first order differential equation
![]()
general and singular solutions .
Solve the equation as
![]()
Let y '= p . Taking the derivative of both sides of the equation with respect to p , we get
![]()
So there is
![]()
which is
![]()
Substitute into the original equation and get a general solution
![]()
from
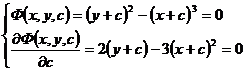
Eliminate c from , and get the c- discriminant curve y=x sum . Substitute it into the original equation directly, we know that y=x is not the solution of the known equation, so it is not a singular solution, but odd solution .![]()
![]()
[ p - discriminant curve method ] For a first-order differential equation , let , then the singular solution of the equation must be included in the following equations![]()
![]()
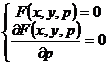
In the curve obtained after eliminating p (called p - discriminant curve) . As for whether the p - discriminant curve is a singular solution, it also needs to be actually tested .
Example of a Differential Equation
![]()
strange solution .
Resolve _
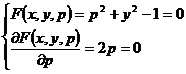
Eliminate p to get the p- discriminant curve , that is, y= . Substitute it into the original equation to know that y= is a singular solution . ![]()
![]()
![]()