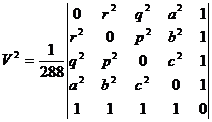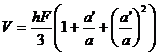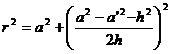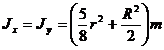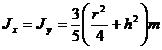§ 4 Volume, surface area and side area of three-dimensional figures
Geometric center of gravity and moment of inertia calculation formula
1.
Calculation formulas for volume, surface area, lateral area, geometric center of gravity and moment of inertia of three-dimensional figures
|
graphics |
Volume V , surface area S , side area M , geometric center of gravity G and moment of inertia *J |
|
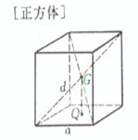
a is the edge length, d is the diagonal
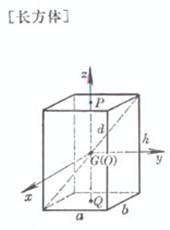
a, b, h are the length , width , height , respectively , d is the diagonal |
volume surface area side area diagonal The center of gravity G is at the intersection of the diagonals volume surface area side area diagonal The center of gravity G is at the intersection of the diagonals Moment of inertia Take the center of the cuboid as the origin of the coordinates , and the coordinates The axis is parallel to the three edges ( At that time , it was the case of a cube ) |
![]() In the table, m is the mass of the object, and the objects are all homogeneous . For the calculation formula of the moment of inertia of general objects, see Chapter VI, § 3 , 5 .
In the table, m is the mass of the object, and the objects are all homogeneous . For the calculation formula of the moment of inertia of general objects, see Chapter VI, § 3 , 5 .
|
graphics |
Volume V , surface area S , side area M , geometric center of gravity G and moment of inertia J |
|
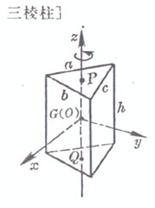
a,b,c are side lengths , h is height
a is the length of the base , h is the height , and d is the diagonal
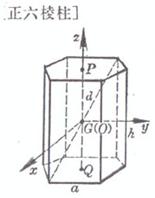
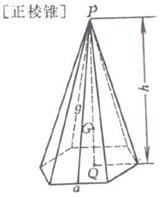
n is the number of edges , a is the base length , h is the height , g is the oblique height |
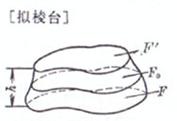
volume surface area side area where F is the area of the base center of gravity ( P and Q are the center of gravity of the upper and lower bottoms , respectively ) Moment of inertia For a regular triangular prism ( a=b=c ), take G as the coordinate origin , and the z - axis is parallel to the edge volume surface area
side area diagonal center of gravity ( P and Q are the center of gravity of the upper and lower bottoms , respectively ) Moment of inertia Take G as the origin of the coordinates , and the z - axis is parallel to the edge volume surface area side area where F is the area of the base , which is the area Center of gravity ( Q is the center of gravity of the bottom surface ) |
|
graphics |
Volume V , surface area S , side area M , geometric center of gravity G and moment of inertia J |
|
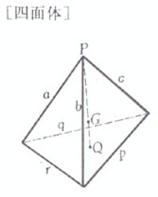
a,b,c,p,q,r is the edge length
h is high
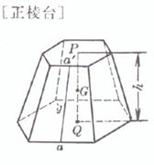
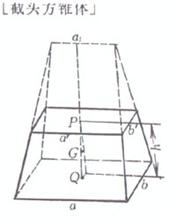
a', a are the lengths of the upper and lower bases , n is the number of edges , h is the height , and g is the oblique height |
volume
center of gravity ( P is the vertex , Q is the center of gravity of the base ) volume where are the areas of the upper and lower bases , respectively center of gravity ( P, Q are the center of gravity of the upper and lower bottoms , respectively ) volume surface area side area where are the areas of the upper and lower bases , respectively center of gravity ( P and Q are the center of gravity of the upper and lower bottoms , respectively ) |
|
graphics |
Volume V , surface area S , side area M , geometric center of gravity G and moment of inertia J |
|
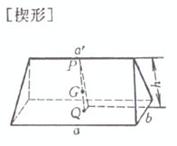
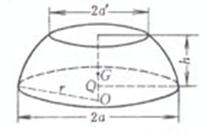
The two bases are rectangular , a', b', a, b are the lengths of the upper and lower bases , respectively , h is the height , which
The base is a rectangle , a and b are the side lengths , h is the height , and a' is the upper edge length
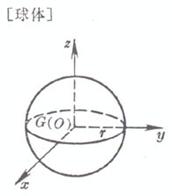
r is the radius |
volume
center of gravity ( P, Q are the center of gravity of the upper and lower bottoms , respectively ) volume center of gravity ( P is the midpoint of the upper edge , Q is the center of gravity of the lower base ) volume surface area The center of gravity G coincides with the center O of the sphere Moment of inertia Take the center of the ball O as the origin of the coordinates |
|
graphics |
Volume V , surface area S , side area M , geometric center of gravity G and moment of inertia J |
|
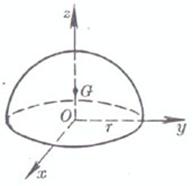
[ hemisphere ]
r is the radius , O is the center of the sphere
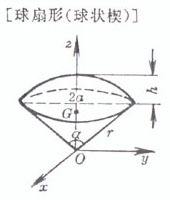
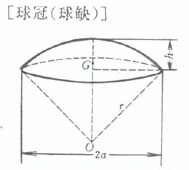
r is the radius of the sphere , a is the radius of the bottom circle of the arch , h is the height of the arch , and
r is the radius of the sphere , a is the radius of the arch bottom circle , and h is the arch height |
volume surface area side area center of gravity Moment of inertia Take the center of the ball O as the origin of the coordinates , and the z - axis coincides with GO volume surface area Side area ( cone surface part ) center of gravity Moment of inertia z -axis coincides with GO volume
surface area Lateral area ( spherical part )
center of gravity |
|
graphics |
Volume V , surface area S , side area M , geometric center of gravity G and moment of inertia J |
|
[ table ]
r is the radius of the ball ,
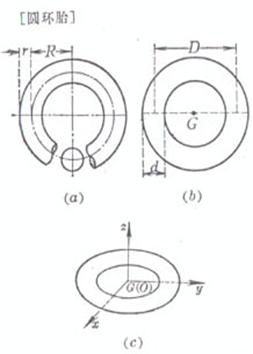
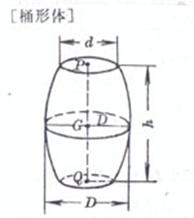
R is the center radius , D is the center diameter , r is the radius of the circular section , d is the diameter of the circular section |
volume surface area side area center of gravity ( Q is the center of the bottom circle ) volume surface area The center of gravity G is on the center of the ring Moment of inertia Take the center of the ring as the coordinate origin , and the z - axis is perpendicular to the plane where the ring is located |
|
graphics |
Volume V , surface area S , side area M , geometric center of gravity G and moment of inertia J |
|
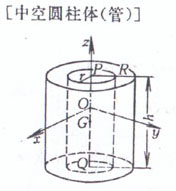
[ cylinder ]
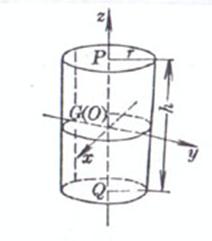
r is the base radius , h is the height
R is the outer radius , r is the inner radius , h is the height
r is the radius of the base circle , h, H are the minimum and maximum heights , respectively, |
volume surface area side area center of gravity ( P and Q are the center of the upper and lower bottom circles , respectively ) Moment of inertia Take the center of gravity G as the origin of the coordinates , and the z - axis is perpendicular to the bottom surface volume surface area side area where t is the wall thickness of the pipe , and center of gravity Moment of inertia Take the z -axis coincident with GQ volume surface area
side area truncated ellipse axis center of gravity ( GQ is the distance from the center of gravity to the bottom , GK
is the distance from the center of gravity to the axis ) |
|
graphics |
Volume V , surface area S , side area M , geometric center of gravity G and moment of inertia J |
|
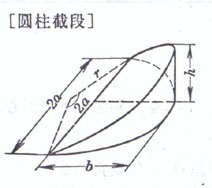
h is the maximum height of the section , b is the arch height of the bottom surface , 2 a is the chord length of the bottom surface , r is the radius of the bottom surface , and
a,b,c are half axes |
volume Lateral area ( cylindrical part ) volume The center of gravity G is on the center O of the ellipsoid Moment of inertia Take the center of the ellipsoid as the origin of the coordinates , and the z -axis coincides with the c -axis
|
|
graphics |
Volume V , surface area S , side area M , geometric center of gravity G and moment of inertia J |
|
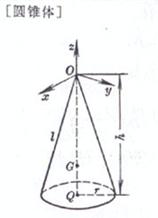
r is the radius of the base circle , h is the height , and l is the busbar
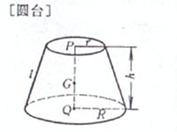
r, R are the upper and lower base circle radius , h is the height , l is the busbar
The upper and lower bases are parallel , |
volume surface area side area busbar center of gravity ( Q is the base circle center , O is the cone vertex ) Moment of inertia Take the vertex of the cone as the origin of coordinates , and the z - axis coincides with GQ volume surface area side area busbar Cone height ( the distance from the intersection of the busbars to the bottom circle ) center of gravity ( P and Q are the center of the upper and lower bottom circles , respectively ) volume [ Note ] Pyramid, circular table, ball table, cone, prism, cylinder, etc. are all special cases of quasi-prism |
|
graphics |
Volume V , surface area S , side area M , geometric center of gravity G and moment of inertia J |
|
d is the diameter of the upper and lower bottom circles , D is the diameter of the middle section , and h is the height |
When the busbar is an arc : volume When the busbar is a parabola : volume center of gravity ( P and Q are the center of the upper and lower bottom circles , respectively ) |
2.
Polyhedron
|
|
[ regular tetrahedron ] |
[ regular octahedron ] |
[ regular dodecahedron ] |
[ Icosahedron ] |
|
graphics |
|
|
|
|
|
face number f |
4 |
8 |
12 |
20 |
|
edge number k |
6 |
12 |
30 |
30 |
|
Vertex number e |
4 |
6 |
20 |
12 |
|
Volume V |
|
|
|
|
|
surface area S |
|
|
|
|
In the table, a is the edge length .
[ Eulerian formula ] The number of faces of a polyhedron is f , the number of edges is k , and the number of vertices is e .
![]()