Introduction
Extend the derivative from natural numbers to all number domains (that is, not only natural numbers
but also negative numbers, decimals, irrational numbers, imaginary or complex numbers, functions, ...),
you can get any order calculus, unifying the world and unifying differentiation and integration into one
formula `d^(o(x))/dx^(o(x)) y`, where o(x) is the order function. When o(x) is a positive integer,
it is a derivative differential. When o(x) is a negative integer, it is an integral. When O(x) is -2,
it is a double integral. When o(x) is a fraction, it is a fractional calculus. When o(x) is a variable,
it is a variable order derivative. These can be calculated with a mathHand.com calculator .
Definition







Property of Fractional Calculus



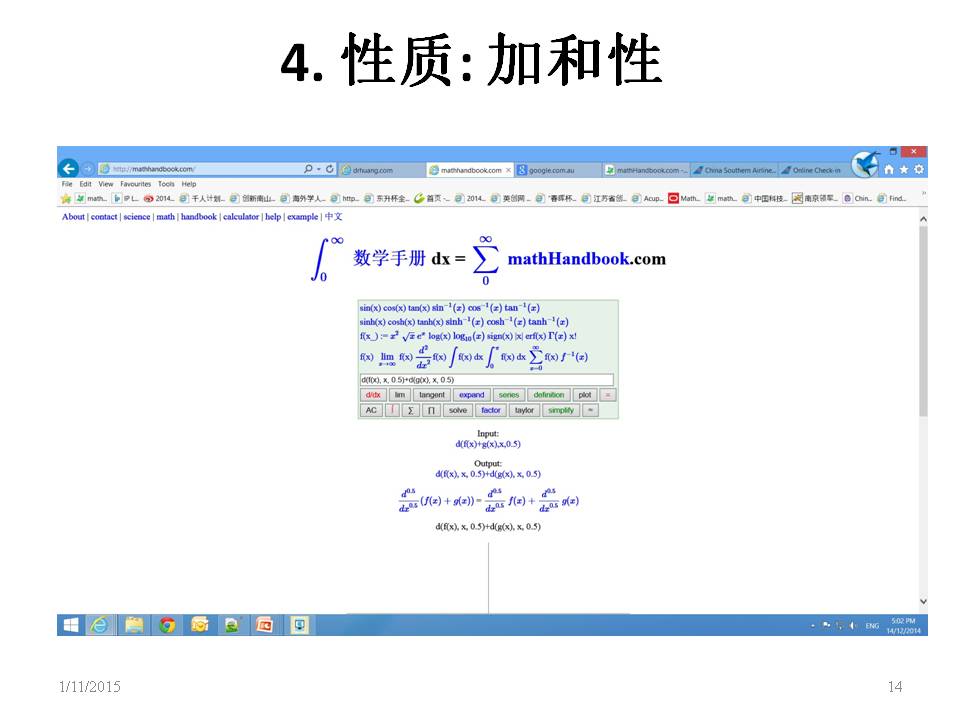
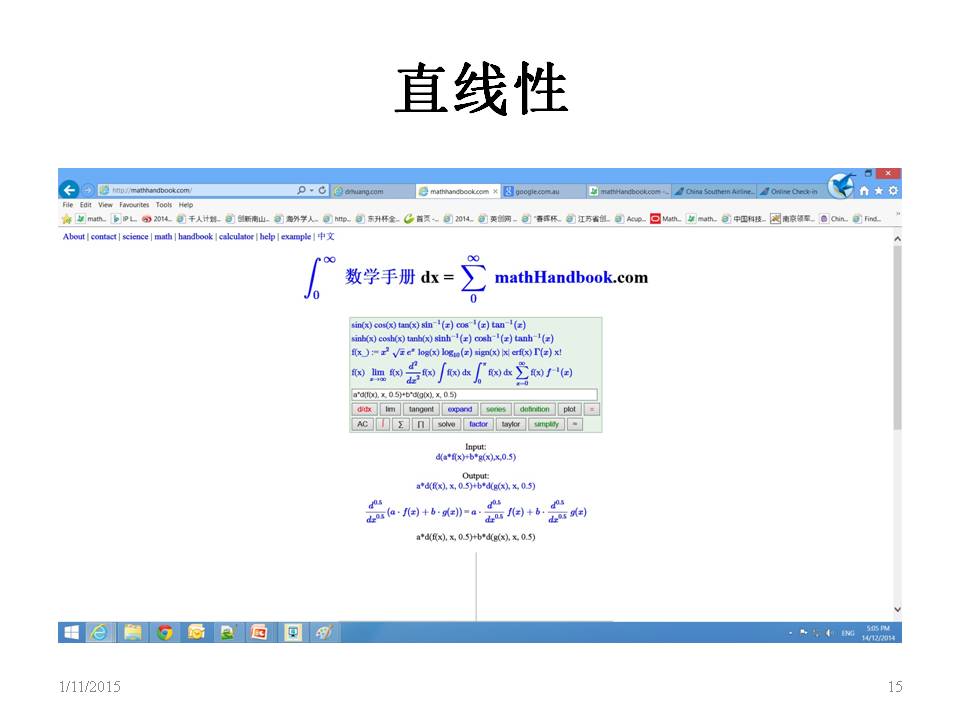
Fractional order derivative is linear as the last figure.
Minus order derivative
As we known, `d^(-1)/dx^(-1) sin(x) = int` sin(x) dx
Fractional order derivative
Input sin(x), click the d^0.5/dx^0.5 button for semiderivative, click the d^0.5/dx^0.5 button again for another semiderivative.
Two times of semiderivative equal to first derivative, e.g.
`d^0.5/dx^0.5 d^0.5/dx^0.5 sin(x) = d^(0.5+0.5)/dx^(0.5+0.5) sin(x) = d/dx sin(x) = cos(x)`
the pi-order derivative
`d^pi/dx^pi - y - 2exp(x)=0 `
Complex order derivative
The order can be extented to complex number a+b i, we differentate by the real order first, then by the imag order.
`d^(a+bi)/d^(a+bi) sin(x) = d^(bi)/dx^(bi) d^a/dx^a sin(x)`.
e.g. the (1+i) order derivative and the (1-i) order derivative equal to second derivative,
`d^(1+i)/dx^(1+i) d^(1-i)/dx^(1-i) sin(x) = d^(1+i+1-i)/dx^(1+i+1-i) sin(x)= d^2/dx^2 sin(x) = -sin(x)`
Variable order derivative
The order can be changed as a function, e.g. the cos(x) order changes between -1 and 1.
`d^cos(x)/dx^cos(x)` sin(x) =
d(sin(x),x,cos(x))
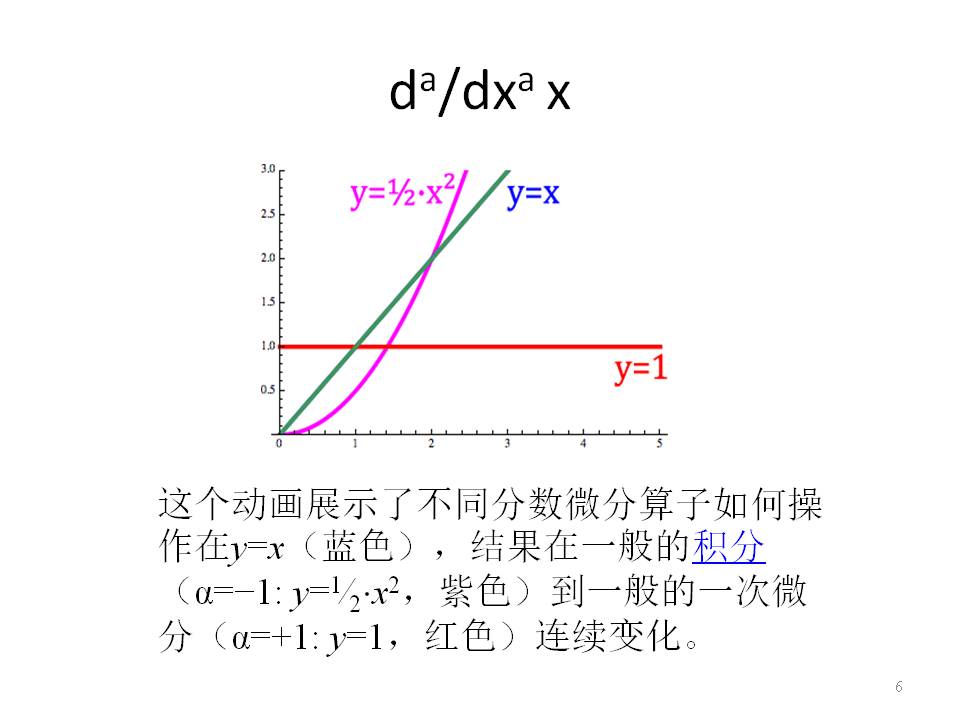
Below, we can see the derivative of y=x changing between its first derivative which is just the constant function y=1 and its first integral (i.e D⁻¹x) which is y=x²/2
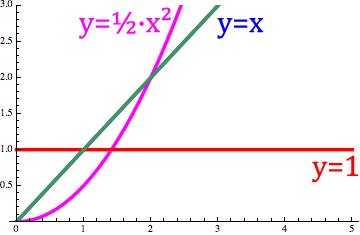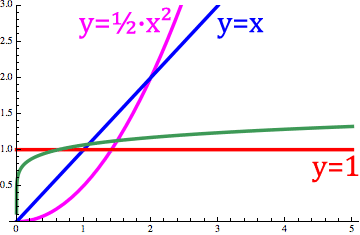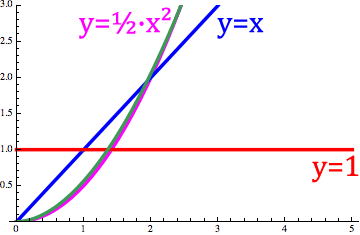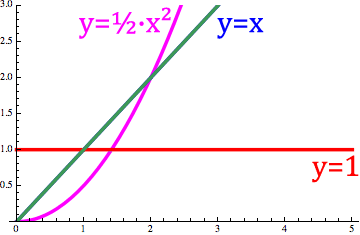
Figure 10. derivative of x with the cos(x) order changed between -1 and 1.
If we pause this animation at the semiderivative, which we calculated above, we get:
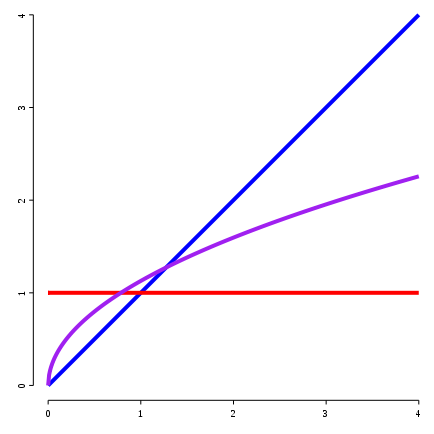
Figure 11. In blue is the function y=x, in red it’s first derivative y=1, and in purple it’s semiderivative.
-
Difference between Caputo definition and the Riemann-Liouville (R-L) definition
The Caputo (Davison-Essex) and the Riemann-Liouville definitions are different in the following aspect: in the Caputo formula, differentiation is performed first, then integration;
but in the R-L formula it is the other way around.
The Caputo definition has advantages over the R-L definition:
1. The Caputo definition implemented maps constants to zero, imitating integer order differentiation and compatible with classic differentiation, while the R-L definition does not.
2. The Caputo definition requires initial value in fractional differential equation is the same as in differential equations, while the R-L definition does not.
3. Its geometric meaning and physical meaning are compatible with classic meaning, while the R-L definition does not.
These properties of the Caputo definition make it suitable to work with initial value problems for fractional differential equations. So the Caputo definition is used here.
-
If you want to use the Riemann defintion, use the Laplace transform solver lasolve( ):
lasolve(y(-0.5,x)=1) give nonzero.
dsolve(y(-0.5,x)=1) give zero.
Fractional dimensional space
Our three-dimensional (3D) space we live in can be extended to the 4-dimensional (4D) space and the n-dimensional space. It also can be extended to fractional dimensional space.
Fractal space has fractal dimension [5] in fractal theory. Fractal dimension corresponds and leads to fractional derivatives. The fractionality in the derivative is due to the fractionality in space.
The exp(x) function in the 1/2-dimensional space is `E_(1/2)(x^(1/2))`, where it is the Mittag-Leffler function. Its fractional derivatives `d^(1/2)/dx^(1/2)` is itself:
`d^(1/2)/dx^(1/2) E_(1/2)(x^(1/2))` =`E_(1/2)(x^(1/2))`
It can be extened to the 1/m-dimensional space:
`d^(1/m)/dx^(1/m) E_(1/m)(x^(1/m))` =`E_(1/m)(x^(1/m))`
When m=1, it becomes exp(x) in one dimensional space.
The geometric meaning of fractional derivatives `d^(1/2)/dx^(1/2) y` is the change rate of y with respect to x in the 1/2-dimensional space.
It can be extened to the 1/m-dimensional space:
the geometric meaning of fractional derivatives `d^(1/m)/dx^(1/m) y` is the change rate of y with respect to x in the 1/m-dimensional space.
Its physical meaning of fractional derivatives is a speed : a point moves from A to B with the speed `d^(1/2)/dt^(1/2)` in the 1/2-dimensional space.
It can be extened to the 1/m-dimensional space:
the physical meaning of fractional derivatives `d^(1/m)/dt^(1/m)` is a speed in the 1/m-dimensional space.
-
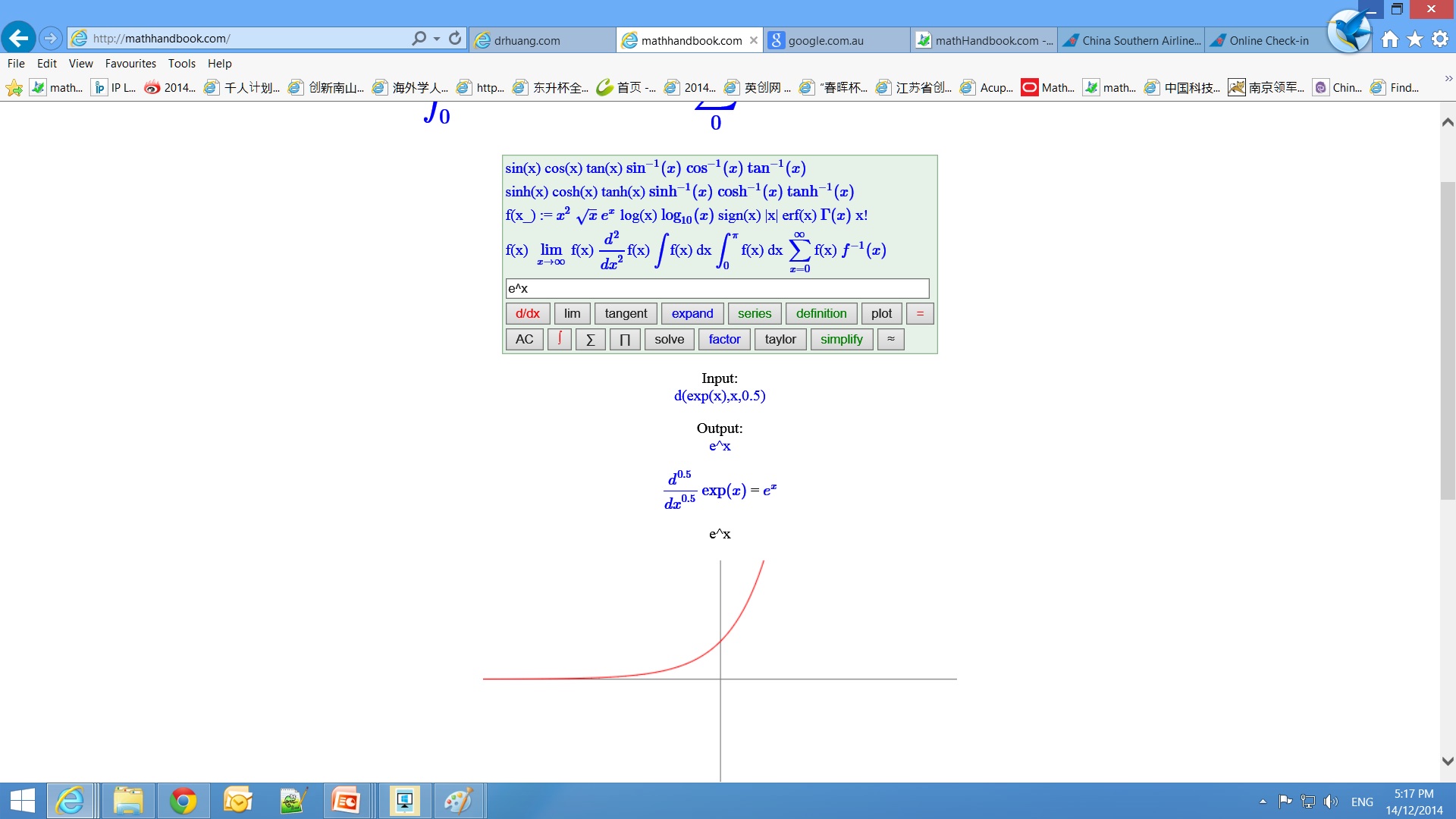
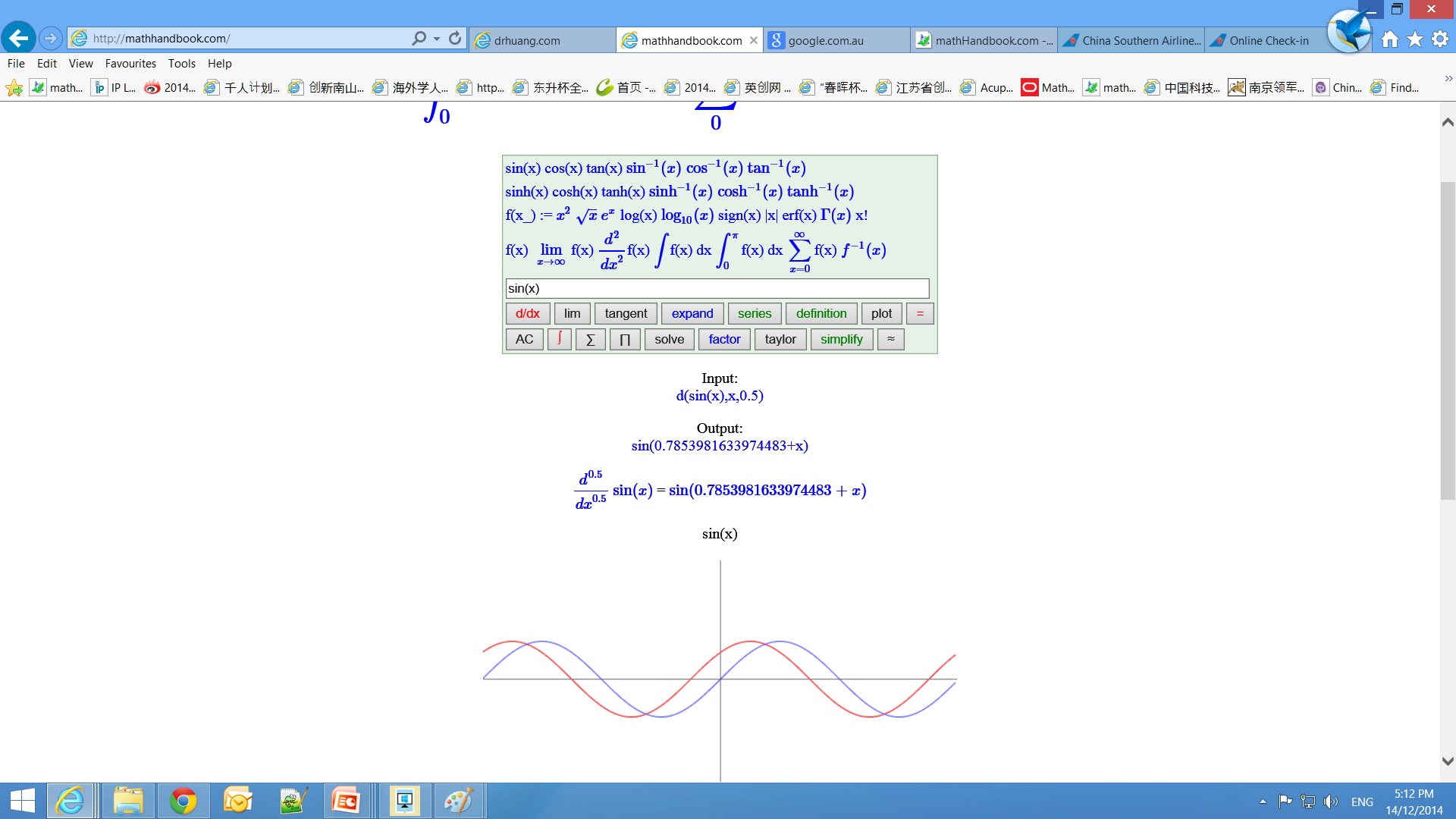
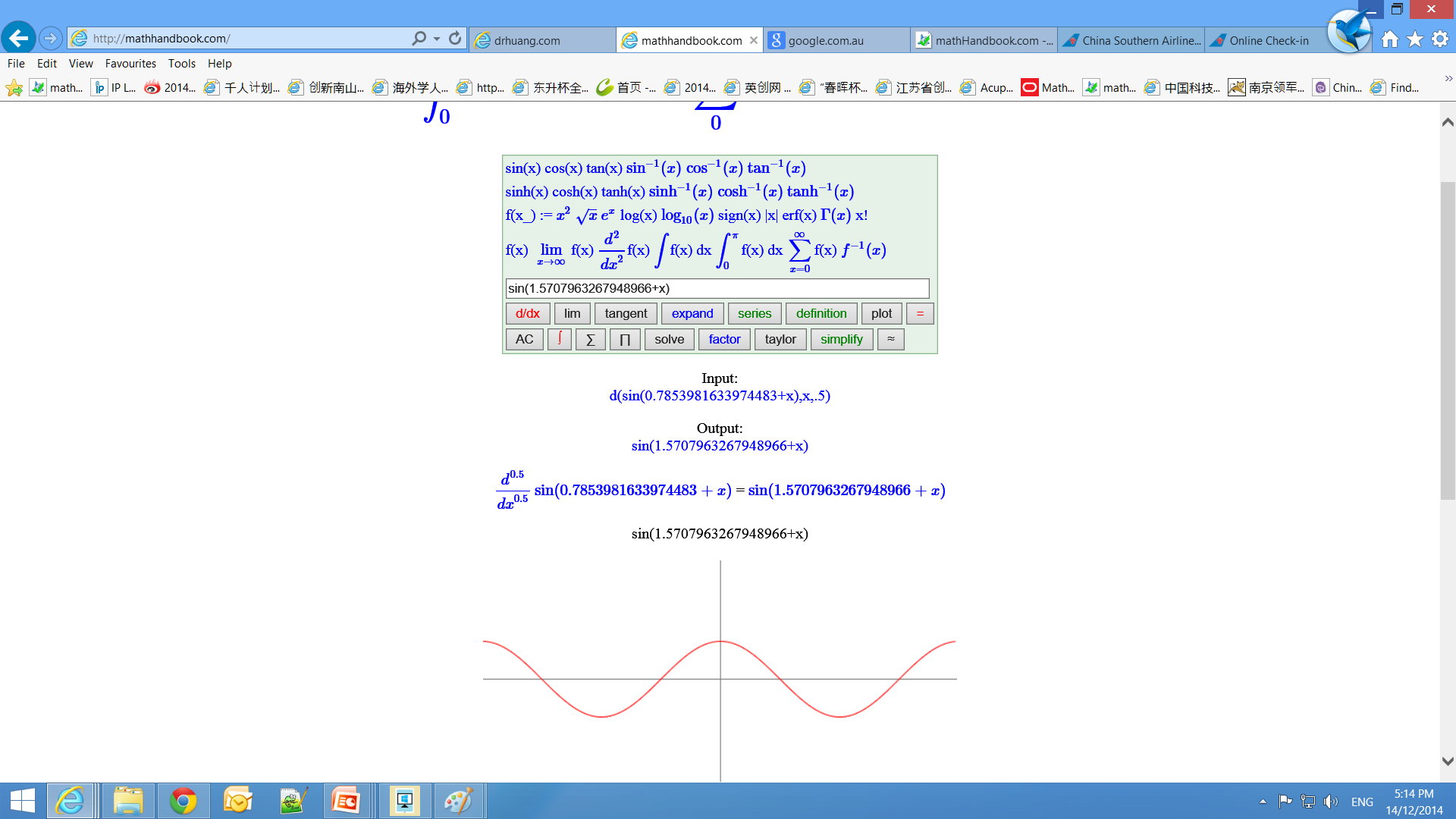
Input Fractional Calculus into Calculator
Input sin(0.5,x) for the 0.5th order derivative of sin(x), which is denoted by `sin^((0.5))(x)`.
It is different from power of sin(x) as `sin(x)^2`.
sin(0.5,x) is semi-order derivative and can be computed and inversed. Computes the 0.5th order derivative of sin(x):
sin(0.5,x) = semid(sin(x)) = d(sin(x),x,0.5)
If you want to hold it (not evaluate), use the derivative holder ds(y,x,0.5).


semi-differentiate graphically
some functions cannot be differentiated symbolically, but can be semi-differentiated graphically for semi-order derivative:
semid2D(sin(x))
=
diff2D(sin(x),x,0.5)
=
ds(x=>sin(x),x,0.5)
Application
In recent years, fractional calculus has been widely used in abnormal diffusion, signal processing and control, fluid mechanics, image processing, soft matter research, seismic analysis, viscoelastic dampers, power fractal networks,
fractional sine oscillators, fractal theory, Fractional PID controller design, electrochemistry. Application of semi-differential in electrochemistry [1-3], overlapping peaks are separated by semi-differential electroanalysis as follows:
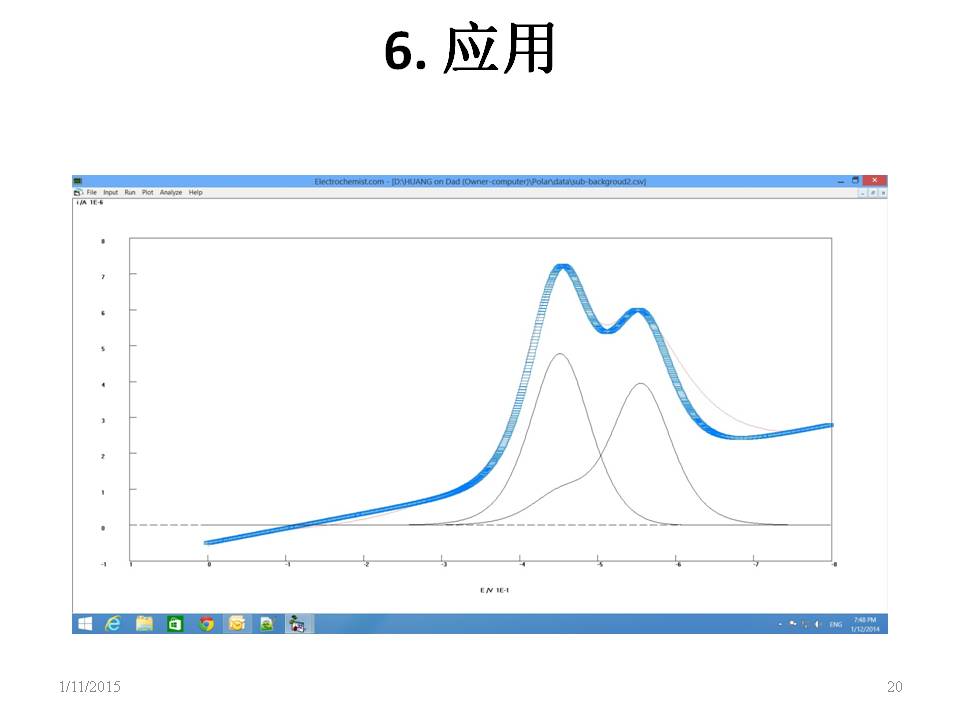
application of fractal theory in electrochemistry [4-6].
-


- J. Mo, P. Cai, W. Huang and F. Yun, Study on the multiple semi-differential electroanalysis of electrochemical stripping method with thin mercury film formed in situ, J. Zhongshan Uni. (Zhongshan Daxue Xuebao), 1984, (4), 76-84, CA 103: 115269.
- J. Mo, P. Cai, W. Huang and F. Yun, Theory and application on multiple semidifferential electrochemical stripping analysis with thin mercury film formed in situ, Acta Chimica Sinica, 1984, 42(6), 556-561, CA 101: 162712.
- J. Mo, W. Huang and R.J. Zhang, New Advances in convolution voltammetry (Review), J. Anal. Determ. (Fenxiceshi Tongbao), 1985, 4(3), 1-8, CA 105: 163910.
- W. Huang and B. Hibbert, Computer modelling of electrochemical growth with convection and migration in rectangular cell, Phys. Rev. E, 1996, 53(1), 727-730.
- J. Jiang, W. Huang and B. Hibbert, Determining fractal dimensions of DLA structures using cumulative randic indices, Physica A, 1996, 233(3-4), 884-887.
- W. Huang and B. Hibbert, Fast fractal growth with diffusion, convection, and migration by computer simulation: Effects of voltage on probability, morphology and fractal dimension of electrochemical growth in a rectangular cell, Physica A, 1996, 233(3-4), 888-896.
- Roubíček, T. (2013), Nonlinear Partial Differential Equations with Applications (2nd ed.), Basel, Boston, Berlin: Birkhäuser, doi:10.1007/978-3-0348-0513-1, ISBN 978-3-0348-0512-4, MR 3014456.
- Samko, S. G. (1987), Fractional Integrals And Derivatives - Theory and Applications, 1987.
- Loverro, Adam (2004), Fractional Calculus - History, Definitions, and Applications for the Engineer, 2004.
- Baleanu, D. and Kumar, D. (2019), fractional calculus and its applications in physics. 2019.
 +
+  +
+  +
+  =
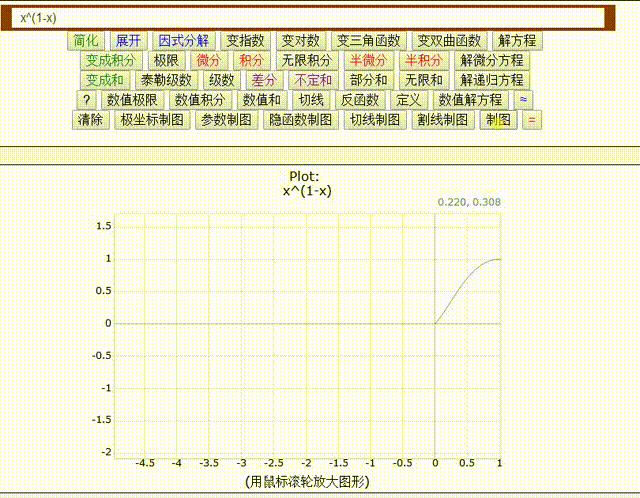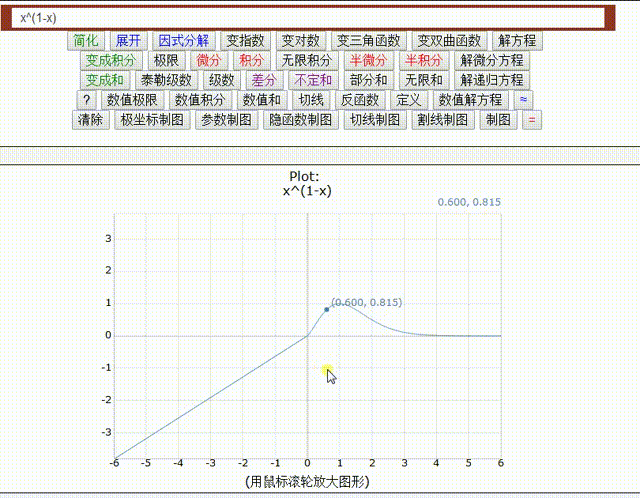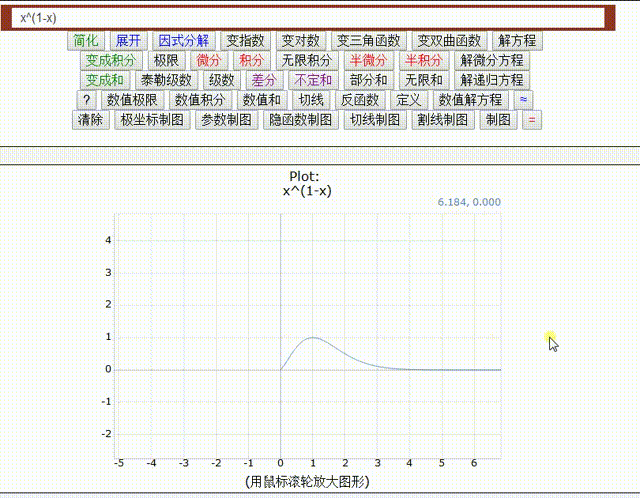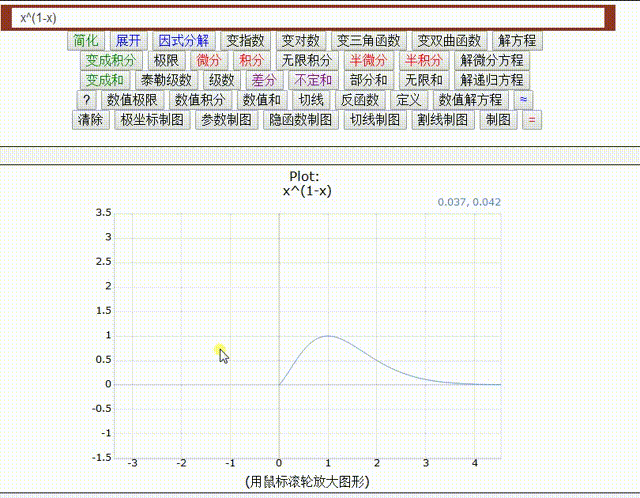
= 
 +
+  +
+  +
+  =
= 



















