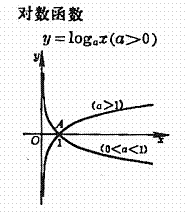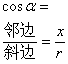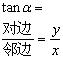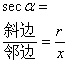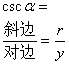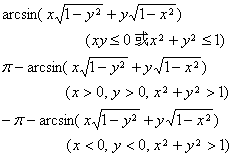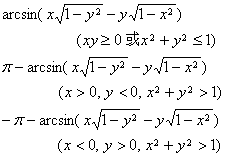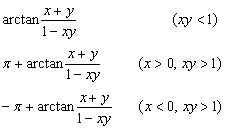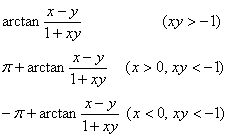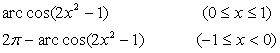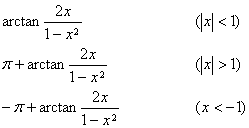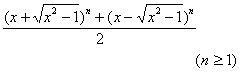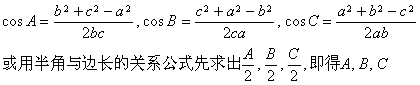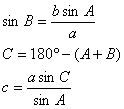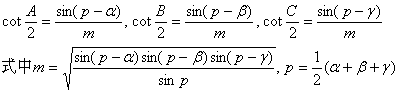§2 elementary function and numerical calculus
First, function concept and classification
[function and inverse function] suppose several volumes which D is assigns. If has two variables x and y, when the variable x takes some specific value when D, variable y also has a definite value according to determination relational f, then said that y is x function, f is called on D functional relations, records is y=f(x), x is called the independent variable, y is called the dependent variable. When x takes in D various numbers, corresponding y constitutes several volume of R, D to be called the domain of definition either the independent variable territory, R is called the value territory or the dependant variable territory. In turn, if regards as the independent variable y, x regards as a dependent variable, writes x expression with y: x=j(y), then said that y=f(x) and x=j(y) are inverse functions mutually.
[real variable function and complex variable function] work as when independent variable territory for real number field, the function is called the real variable function. When independent variable territory for complex field, the function is called the complex variable function.
[a circular function and function of many variables] only then an independent variable's function is called a circular function. Two or two above independent variable's functions are called the function of many variables.
[explicit function and implicit function] the dependent variable may express directly by the independent variable with mathematics formula the function is called the explicit function. If the functional relations contain in an equation or group of equations, the independent variable and the dependent variable differentiate not obviously, is called the implicit function.
[simple function and composite function], if y is u function y=f(u), but u is also x function, u=j(x), then y is called x composite function, u is called the middle variable, records makes y=f[j(x)], not middle variable's function is called the simple function.
[limited function and unbounded function], if has two to count m, M(m£M), causes m£f(x)£M, x establishes willfully to the domain of definition, then said that f(x) is in the domain of definition limited function, m is its world of mortals, M is its upper boundary. If such number m and M have one not to exist at least, then said that f(x) is in the domain of definition unbounded function.
[monotone function with non-monotone function], if regarding the sector [a, b] random x1>x2 has f(x1) ³ f(x2) [or f(x1)£f(x2)], then said that f(x) is [a, b] the increasing function (or decreasing function). The increasing function and the decreasing function are generally called for the monotone function. It is not the increasing (or decreasing progressively) the function is called the non-monotone function.
[odd function and even
function], if
x has permanently
willfully regarding the domain of definition,![]() then said that
f(x) is an odd
function; If x has permanently willfully regarding the domain of
definition,
then said that
f(x) is an odd
function; If x has permanently willfully regarding the domain of
definition,![]() then said that f(x) is an even function.
then said that f(x) is an even function.
[periodic function with non-periodic function], if has a real number T ¹ 0, enables x to have permanently willfully to the domain of definition in f(x+T)=f(x), then f(x) is called take T as the cyclical periodic function; Otherwise said that f(x) is the non-periodic function.
[monodrome function and multiple-valued function], if regarding an independent variable x value, dependent variable y has one moreover only then a value with its correspondence, then said that y is x monodrome function. If regarding an independent variable x value, continues with its correspondence's y value, then said that y is x multiple-valued function.
[elementary function] the power function, the exponential function, the logarithmic function, the trigonometric function, the inverse trigonometric function are generally called for “the basic elementary function”, everything has the time limit mathematical operations by the basic elementary function process as well as has the time limit compound step to constitute, and can use the function which a mathematics formula expressed to belong to the elementary function.
Second, power function and rational function
[definition] the shape like![]() function is called the power
function, in the formula a for willfully the solid
constant.
function is called the power
function, in the formula a for willfully the solid
constant.
x multinomial
![]()
(a0, a1, L, an is constant, n is natural number)
Is called the rational integral function.
Two multinomial business
![]()
Is called the rational fraction function.
The rational integral function and the rational fraction function are generally called for the rational function, sometimes uses mark R(x) to indicate.
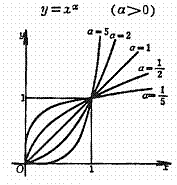
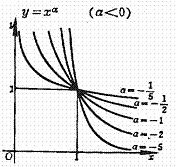
[power function graph and characteristic]
|
Equation and graph |
Especially Drafting |
|
|
Curve initial point (0,0) and (1,1); When x>1, a bigger curve rise is quicker. When a is an even number, the function is an even function, in the sector in (0,¥) is the increasing function, in sector (- ¥, 0) for decreasing function. When a is an odd number, function for odd function and increasing function. |
|
|
Curve initial point (1,1). When a is at bay counts, the function is an even function, in the sector (- ¥, 0) is the increasing function, in sector (0, ¥) for decreasing function. When a is negative odd number, function for odd function and decreasing function. |
Third, exponential function and logarithmic function
[definition] the shape like![]() function is called the exponential
function.
function is called the exponential
function.
When a=e, is writing
is convenient, sometimes![]() records does expx,
records does expx, ![]() records
makes exp{f(x)}, and so
on.
records
makes exp{f(x)}, and so
on.
In function relationship![]()
![]() ,
if x regards as
the independent variable, y regards as a dependent variable, then said
that y is
take a as the
bottom x logarithmic function,
x is called the
logarithm, records does
,
if x regards as
the independent variable, y regards as a dependent variable, then said
that y is
take a as the
bottom x logarithmic function,
x is called the
logarithm, records does![]() . The
exponential function and the logarithmic function are inverse functions
mutually.
. The
exponential function and the logarithmic function are inverse functions
mutually.
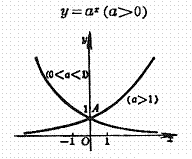
[functional digraph and characteristic]
|
Equation and graph |
Especially Drafting |
|
Exponential function
|
Curve and y axis intersection in A(0,1). The approach line is y=0. |
|
|
Curve and x axis intersection in A(1,0). The approach line is x=0. |
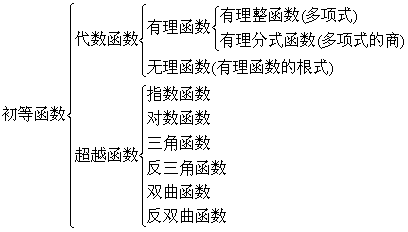
[index operation principle]
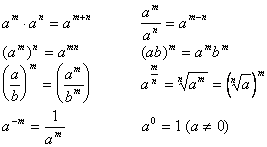
simultaneously [logarithm nature and operation principle] in the following formula, supposition a>0, the function supposition which meets are discuss in the domain of definition.
Zero and the negative number do not have
the
logarithm
![]()
![]()
![]()
![]()
![]()
Logarithm identical equation
![]() Trades the bottom formula
Trades the bottom formula ![]()
![]()
[common logarithm and natural logarithm]
1o common logarithm: Take 10 are called the common logarithm as the bottom logarithm, records does
![]()
2o natural logarithm: As the bottom logarithm is called the natural logarithm take e=2.718281828459L, records does
![]()
3o common logarithm and natural logarithm relations:
![]()
In the formula M is called the modulus,
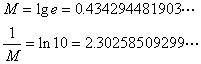
the 4o common logarithm first number asks the law:
If the logarithm is bigger than 1, then logarithm first number for positive number or zero, its value compared to integer figure few 1.
If the logarithm is smaller than 1, then the logarithm first number is a negative number, its absolute value is equal to front of the logarithm first place significant digit “0” integer (before decimal point that “0”).
The logarithm mantissa finds out by the logarithmic table.
Fourth, plane trigonometry function and inverse trigonometric function
1. Angle measure and conversion
[angle system and radian system]
1o entire circumference![]() the arc
is called includes 1 degree arc, but 1 degree arc to the center of circle angle is
called 1 degree
angle .1 degrees to be
equal to that 60 points (record do
the arc
is called includes 1 degree arc, but 1 degree arc to the center of circle angle is
called 1 degree
angle .1 degrees to be
equal to that 60 points (record do![]() ), 1 classification (records in 60 seconds does
), 1 classification (records in 60 seconds does![]() ). This kind with measures the angle the method to
be called the angle system.
). This kind with measures the angle the method to
be called the angle system.
2o was equal to that the radius long arc is called includes 1 radian arc, but 1 radian arc to the center of circle angle is called 1 radian the angle, this kind measures the angle with the radian the method to be called the radian system.
[and radian conversion] radian and the relations are
![]()
In the formula q and a express the identical angle number of degree and the radian number separately.
And radian conversion tableⅠ
|
Radian (r) |
(°) |
Minute (¢) |
Second (²) |
|
1 |
57.29577951 |
3437.746771 |
206264.8063 |
|
0.017453293 |
1 |
60 |
3600 |
|
0.0002908882 |
0.016666667 |
1 |
60 |
|
0.0000048481 |
0.000277778 |
0.016666667 |
1 |
![]() . In the table the
blackbody digit is the precise value.
. In the table the
blackbody digit is the precise value.
And radian conversion tableⅡ
|
360° |
180° |
90° |
60° |
45° |
30° | |
|
Radian |
|
|
|
|
|
|
[the ancestor rate (girth quotient) p] the circle perimeter and diameter ratio is called the girth quotient, expressed with the p. Because our country ancient times Southern Dynasty's mathematician Zu Chongzhi achieved the glorious triumph in the computation girth quotient aspect, thus the girth quotient also often was called the ancestor rate.
![]()
Zu Chongzhi figures out p the value is 3.1415926<p<3.1415927.
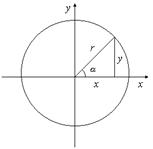

2. Trigonometric function definition
[trigonometric function definition and sign modification]
|
Name |
Sine |
Cosine |
Tangent |
Cotangent |
Secant |
Cosec | ||
|
Deciding Righteousness |
|
|
|
|
|
| ||
|
Symbol Number With |
Increasing Reducing Changing Melting |
Ⅰ |
+↑ |
+↓ |
+↑ |
+↓ |
+↑ |
+↓ |
|
Ⅱ |
+↓ |
- ↓ |
- ↑ |
- ↓ |
- ↑ |
+↑ | ||
|
Ⅲ |
- ↓ |
- ↑ |
+↑ |
+↓ |
- ↓ |
- ↑ | ||
|
Ⅳ |
- ↑ |
+↑ |
- ↑ |
- ↓ |
+↓ |
- ↓ | ||
[trigonometric function graph and characteristic]
Standard sine curve
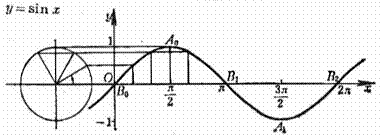
Cycle:![]()
With x axis point of intersection (same inflection point):
![]()
Extreme point (maximum point or minimum point):
![]()
Cosine curve
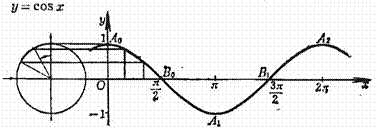
Cycle:![]()
With
x axis point of
intersection (same inflection point):![]()
Extreme
point:![]()
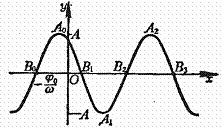
Generally sine curve
![]() Cycle:
Cycle:![]()
In the formula
A>0 is an
oscillation amplitude, ![]() is the angular frequency,
is the angular frequency, ![]() is the
first
phase
With x axis point of intersection (same inflection
point):
is the
first
phase
With x axis point of intersection (same inflection
point):
|
|
![]()
Extreme point:

![]()
At the same time, ![]() also
belongs to the general sine tune
It is extends the
standard sine curve in the y axis direction
also
belongs to the general sine tune
It is extends the
standard sine curve in the y axis direction
The line
(supposes![]() , may
change into)
, may
change into) ![]() Long A time, compresses time in
x axis direction
Long A time, compresses time in
x axis direction![]() ,
and
,
and
Translates![]() section of distances to obtain toward
left.
section of distances to obtain toward
left.
Tangent curve
y=tan x
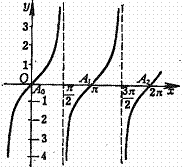 Cycle:
Cycle:![]()
With x axis point of intersection (same inflection point):
![]() ,
,
This tangent slope is 1.
Approach line:![]()
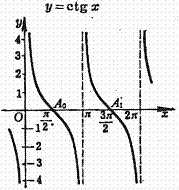
Cotangent curve
|
|
Cycle:![]()
With x axis point of intersection (same inflection point):
![]() ,
,
This tangent slope is - 1.
Approach line:![]()
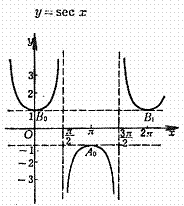
Secant curve
|
|
Cycle:![]()
Maximum point:![]()
Minimum point:![]()
Approach line:![]()
Cosec curve
|
|
Cycle:![]()
Maximum point:![]()
Minimum point:![]()
![]()
Approach line:![]()
3. Special angle triangle function value
|
|
|
|
|
|
|
| |
|
Radian | |||||||
|
0 |
|
0 |
1 |
0 |
|
1 |
|
|
15 |
|
|
|
|
|
|
|
|
18 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
Radian | |||||||
|
22.5 |
|
|
|
|
|
|
|
|
30 |
|
|
|
|
|
|
2 |
|
36 |
|
|
|
|
|
|
|
|
45 |
|
|
|
1 |
1 |
|
|
|
54 |
|
|
|
|
|
|
|
|
60 |
|
|
|
|
|
2 |
|
|
67.5 |
|
|
|
|
|
|
|
|
72 |
|
|
|
|
|
|
|
|
75 |
|
|
|
|
|
|
|
|
90 |
|
1 |
0 |
|
0 |
|
1 |
|
120 |
|
|
|
|
|
|
|
|
135 |
|
|
|
|
|
|
|
|
150 |
|
|
|
|
|
|
2 |
|
180 |
|
0 |
|
0 |
|
|
|
In the table![]() indicated
indicated![]() that
(i.e. left and right limit) 0.1 acute angle's coangle's triangle function value
is equal to this angle -odd triangle function value, for example
that
(i.e. left and right limit) 0.1 acute angle's coangle's triangle function value
is equal to this angle -odd triangle function value, for example![]()
![]()
![]() .
.
4. Trigonometric function basic relations and formula
[induction formula]
Trigonometric function induction formula table
|
Function Angle |
sin |
cos |
tan |
cot |
sec |
csc |
|
|
|
|
|
|
|
|
|
Function Angle |
sin |
cos |
tan |
cot |
sec |
csc |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
In the table n is an integer.
[basic relations]
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Trigonometric function reciprocity table
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
For example, if![]() , then
, then![]()
[addition formula]
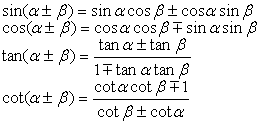
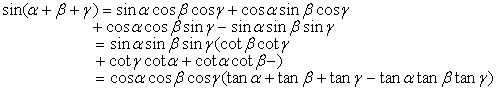
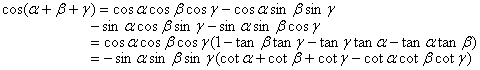
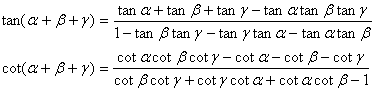
[and difference and accumulates melts formula mutually]
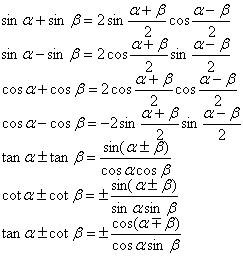
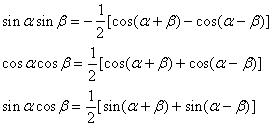
[double angle formula]

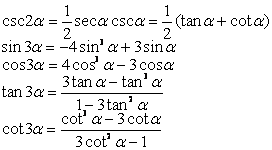

In the formula n is a positive integer.
[half-angle formulas]
In the following formula the root number institute takes the mark to be consistent with equal sign left side of mark.
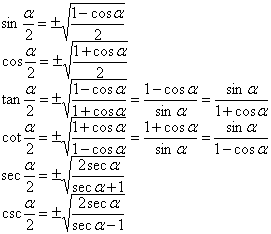
[descending powers formula]


Above in the formula n is a positive integer.
[trigonometric function is limited and formula]


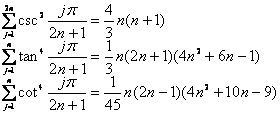
5. Inverse trigonometric function definition
[inverse trigonometric function domain of definition and principal value scope]
|
Function |
Principal value symbol |
Domain of definition |
Principal value scope |
|
Anti-sine |
If |
|
|
|
Arc |
If |
|
|
|
Counter-tangent |
If |
|
|
|
Arc |
If |
|
|
|
Arcsec |
If |
|
|
|
Arc |
If |
|
|
Generally the inverse trigonometric function and the principal value relations are
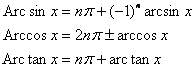
In the formula n is the random integer.
[inverse trigonometric function graph and characteristic]
Anti-sine curve Arc curve
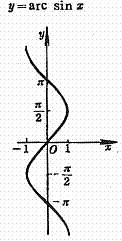
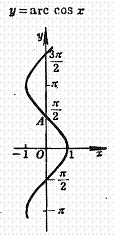
Inflection point (same curve center of symmetry): Inflection point (same curve center of symmetry):
![]() , this tangent slope is
1
, this tangent slope is
1
![]() , this tangent slope is -
1
, this tangent slope is -
1
Counter-tangent curve Arc curve
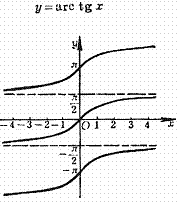
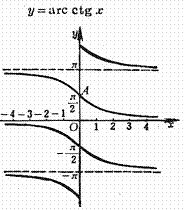
Inflection point (same curve center of symmetry): Inflection point:
![]() , this tangent slope is
1
, this tangent slope is
1
![]() , this tangent slope is -
1
, this tangent slope is -
1
Gradually coil in:![]() Curve center of symmetry:
Curve center of symmetry:![]()
Approach line:![]()
Arcsec curve Arc curve
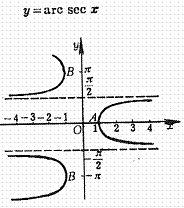
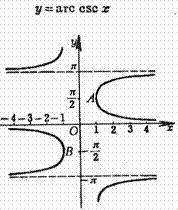
Apex:![]() Apex:
Apex:![]()
Approach line:![]() Approach
line:
Approach
line:![]()
6. Inverse trigonometric function reciprocity and fundamental formula
[inverse trigonometric function reciprocity]
|
arc sin x = |
arc cos x = |
arc tan x = |
arc cot x = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Has * the number when only x for just when is suitable.
[inverse trigonometric function fundamental formula]
|
arc sin x + arc sin y = |
arc sin x - arc sin y = |
|
|
|
|
arc cos x + arc cos y = |
arc cos x - arc cos y = |
|
|
|
|
arc tan x + arc tan y = |
arc tan x - arc tan y = |
|
|
|
|
2 arc sin x = |
2 arc cos x = |
|
|
|
|
2 arc tanx = |
cos (n arc cos x) = |
|
|
|
7. Triangle fundamental theorem
|
|
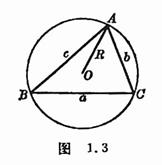
[sine law]
![]()
In the formula
R is![]() the ABC external
connection radius (Figure 1.3).
the ABC external
connection radius (Figure 1.3).
[law of cosines]
|
|

[pythagorean theorem] in the right triangle (C is right angle), cancels Fang Jiagu the side to be equal to the string side (Figure 1.4), namely
![]()
The pythagorean theorem also said that the business high theorem, in the foreign books and periodicals calls Pythagoras the theorem.
[tangent theorem]
![]()
Or
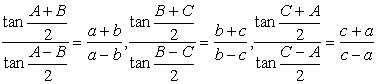
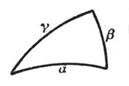
[half-angle and length of side relational formula]
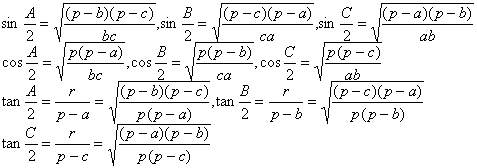
In the formula![]() , r
is
, r
is![]() the ABC
interior contact radius, and
the ABC
interior contact radius, and
![]()
In the formula
S is![]() the ABC area.
the ABC area.
8. Oblique triangle solution
|
Known element |
Other elements ask the law | |
|
At the same time a and two jiao B, C |
| |
|
Two side a, b and included angle C |
| |
|
Trilateral a, b, c |
| |
|
Two side a, b and one side opposite angle A |
|
when b sin A<a, has two solutions when b sin A>a, non solution when b sin A=a, has a solution |
Fifth, spherical trigonometry
|
|
1. Spherical trigonometry related name and nature
[great-circle] with one intercepts a pass through the center O plane, is called the great-circle in the ball surface obtained transversal, its radius is equal to the ball radius R (Figure 1.5).
[great-circle arc length]
connects in the spherical surface
two A, the B geodetic line
is passes A, in the
B great-circle the
short arc![]() , its center of circle angle for a (by radian idea), then
, its center of circle angle for a (by radian idea), then![]() arc length a
= Ra.
arc length a
= Ra.![]()
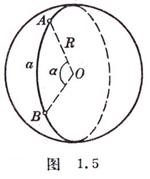
[two great circle arc included angles] on two great circle arc's point of intersection A corresponding great-circle's tangent (the AB', AC') included angle is called these two great circle arcs the included angle, its also available two plane OAB and OAC constitute the dihedral angle measures (Figure 1.6).
|
|
[spherical surface two angular area]
the spherical surface two
angular ABA'C area (Figure 1.6 dashed area)![]() (A is two great
circle arc included angles, unit is radian).
(A is two great
circle arc included angles, unit is radian).
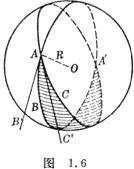
[spherical triangle spherical excess (or spherical angle surplus)] Three great-circles may constitute several spherical triangles in the spherical surface, we only considered that which triangles trilateral and is smaller than p.
|
|
Supposes a, b, g is nearby three (i.e. three section of great-circle arc lengths, take radius R as Unit of measurement), A, B, C is three angles (i.e. three section of great circle arc 22 included angles, Figure 1.7). The spherical triangle's sums of three angle are certainly bigger than 180°, its difference d = A + B + C-p calls the spherical excess (unit radian), d >0.
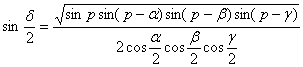
In the formula![]() .
.
[spherical triangle area] spherical triangle ABC (Figure 1.7 dashed area) area S = R2d.
2. Spherical triangle fundamental theorem and formula
[sine law]
![]()
[law of cosines]
:![]()
Angle:![]()
[cotangent theorem]
:![]()
Angle:![]()
[tangent theorem]
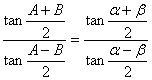
[five element formulas]
:![]()
Angle:![]()
[half-angle formulas]
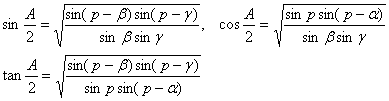
In the formula![]() .
.
[half-side formula]
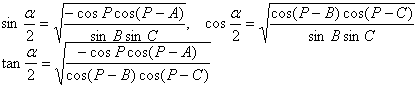
![]()
[Delane cloth - Gaussformula]
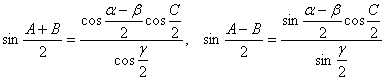
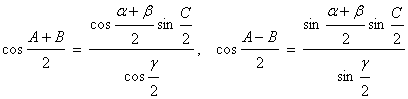
[Napier formula]
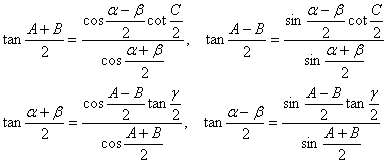
3. Spherical triangle solution
[general spherical triangle formula]
|
Known element |
Solution formula |
|
Trilateral: a, b, g
|
|
|
Triangle: A <> |