§ 2 Generalized Fourier series and Fourier - Bessel series

 

1. Generalized Fourier Series

 

If the continuous function is

                                               ( 1 )

Orthogonal on a certain interval , and if the function is absolutely integrable on , then the

                     

is the series of coefficients

                         

is called the generalized Fourier series of functions with respect to the orthogonal function system ( 1 ) , denoted as

                      f ( x ) ~

are called the Fourier coefficients of the orthogonal function system ( 1 ) .

    Let ( 1 ) be a standard orthogonal function system, that is, it satisfies

                           

then

                        

At this time, with respect to, there is Bessel's inequality

                            ( is a square integrable function  

If for any square-integrable function, the closedness equation

                       

It is said that the orthogonal function system at this time is closed .

 

2. Fourier - Bessel series

 

    [ Fourier - Bessel series ]

1   Let ^o be the positive root of the Bessel function (see Chapter 12), then the function system

Orthogonal by weight x on [0, 1] , i.e.

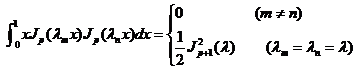
    2 ^o  For all functions that are absolutely integrable on [0, 1] , its Fourier - Bessel series can be made

f ( x ) ~

in the formula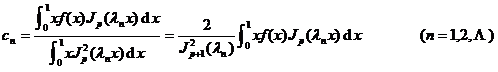       

are called the Fourier - Bessel coefficients of a function .

    3 ^o  If it is continuous everywhere on [0, 1] except for a finite number of discontinuous points of the first kind and is segment-wise differentiable, then its Fourier - Bessel series converges at that time, and at the continuous points, the series The sum equals , at the discontinuity, the series sum equals ;

If it is absolutely integrable on [0 , 1] , continuous in the interval and has absolutely integrable derivatives, then its Fourier-Bessel series converges uniformly in every interval ;

If it is absolutely integrable over [0 , 1] , continuous over the interval and has absolutely integrable derivatives, at the same time , then its Fourier - Bessel series converges uniformly over every interval .

[ Fourier - Bessel series of the second kind ]

1 ^o  Let it be

                                 ( H is a constant)

The positive root of , then, at that time , the function system

                  

Orthogonal by weight x on [0, 1] .

    If it is absolutely integrable on [0 , 1] , then its generalized Fourier series with respect to the above orthogonal system is called a Fourier - Bessel series of the second kind , namely

                      ~

in the formula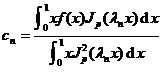        

            

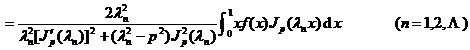
    2 ^o  If the function is piecewise differentiable on [0, 1] (with at most a finite number of discontinuities of the first kind), then its Fourier - Bessel series of the second kind converges on 0 < x < 1 , and Equal at continuous points and equal at discontinuous points ;

If the function is continuous on [0 , 1] , twice differentiable (except for a finite number of points), and = 0, , bounded, then its second kind of Fourier - Bessel series is then , at each The interval [ ,1] (0< <1) is absolutely and uniformly convergent; at the same time , it is absolutely and uniformly converged on the entire interval [0 , 1] .

    [ Fourier - Bessel series over the interval [0 , l ] ]

    Suppose it is absolutely integrable on [0 , l ] , then its Fourier - Bessel series is

                                       f ( x ) ~

in the formula                        

For the Fourier - Bessel series of the second kind,

          

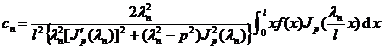
Regarding the convergence of the series, we can only discuss the convergence of the corresponding Fourier - Bessel series on [0 , 1] by transforming , .