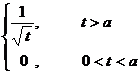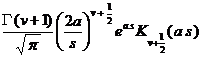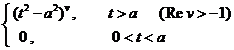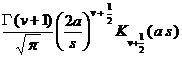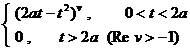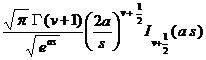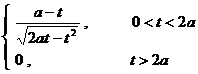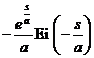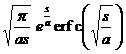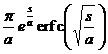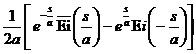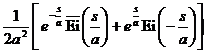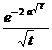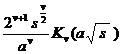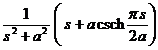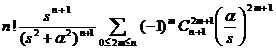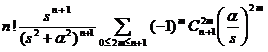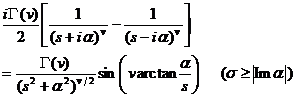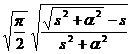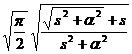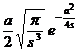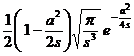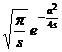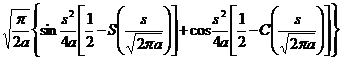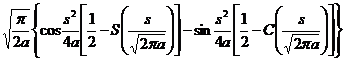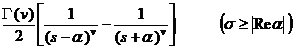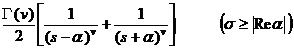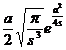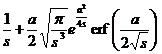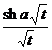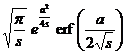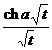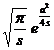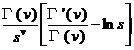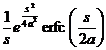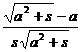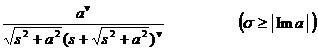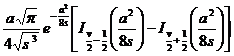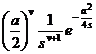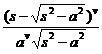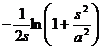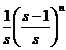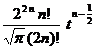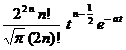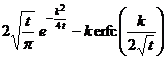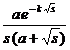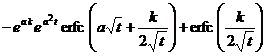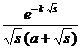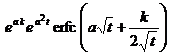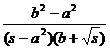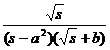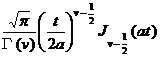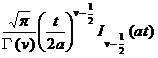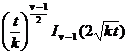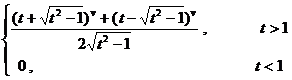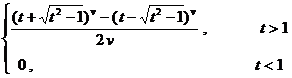§3 Laplace transform
Laplace transform of [ Laplace transform and its inversion formula ] ![]()
![]() ( s is a complex number, s = )
( s is a complex number, s = )![]()
Inversion formula of Laplace transform
![]()
![]()
![]()
The integral is taken along any straight line Res= ![]() , which is the growth index, and at the same time, the integral is understood in the sense of the principal value .
, which is the growth index, and at the same time, the integral is understood in the sense of the principal value .![]()
![]()
[ Conditions for the existence of Laplace transform ] If the following three conditions are satisfied, then its Laplace transform exists .![]()
(i)
The complex-valued function sum of real variables is continuous except for the discontinuous points of the first type (there are at most a finite number in any finite interval);![]()
![]()
![]()
(ii)
when t < 0 , =0;![]()
(iii)
is of finite order, that is to say it is possible to find constants and A > 0 such that![]()
![]()
![]()
![]()
The number here is called the growth index, and when it is a bounded function, it can take =0.![]()
![]()
![]()
![]()
If the above three conditions are satisfied, then L ( s ) is an analytic function on the half-plane Res> ![]() . The inversion formula holds at the continuous points of .
. The inversion formula holds at the continuous points of .![]()
[ Properties of Laplace Transform ]
![]() ( a is a constant )
( a is a constant )
![]() ( a , b are constants )
( a , b are constants )
![]()
in the formula
![]()
is called the convolution (or convolution) of the function and g ( t ) .![]()
[ Main formula table of Laplace transform]
|
original function |
Laplace transformed function |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f ( n ) ( t )
|
|
|
|
|
|
|
|
|
original function |
Laplace transformed function |
|
|
|
|
|
( ) m s n L ( m ) ( s ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
f ( t 2 ) |
|
|
t v- 1 f ( t )
(Re v > ) |
|
|
|
|
|
|
L (ln s ) |
|
|
|
|
|
|
|
|
|
|
|
|
[Laplace transformation table]
![]()
![]()
![]()
![]()
Laplace Transformation Table I
(It is convenient to use this table to find the Laplace transform of a known function)
|
f ( t ) |
L ( s ) |
|
|
1 |
|
|
e – cs |
|
1 |
|
|
t |
|
|
t n
|
|
|
|
|
|
t v
( Rev > ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( 2 t + t 2 ) v ( a >0, Rev > ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e a t |
|
|
te a t |
|
|
t n e a t
|
|
|
t v e a t (
Rev > ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ln t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
erf ( a t ) ( a >0 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Laplace Transformation Table II
(The Laplace transform of a known function is convenient to use this table to check its original function)
|
L ( s ) |
f ( t ) |
|
|
|
|
|
|
|
( varies) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( ) |
|
|
|
|
|
|
[ Double Laplace transform and its inversion formula ]
The double Laplace transform of the function f ( x,y ) is
![]()
The inversion formula of the double Laplace transform is:
![]()
Among them .![]()
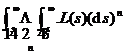
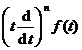
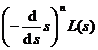
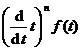
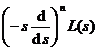

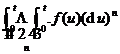
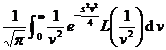
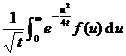
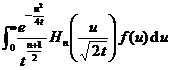
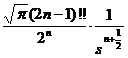
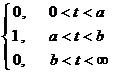
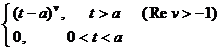
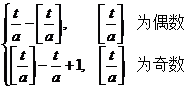 ( a > 0)
( a > 0)