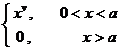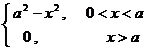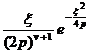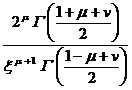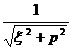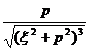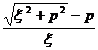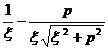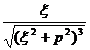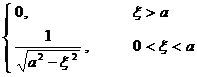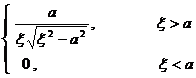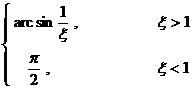§7 Hankel Transform
[ Hankel transform and its inversion formula ]
The v -order Hankel transform of
The inversion formula of the v -order Hankel transform is:
where J v ( x ) is a Bessel function .
[ Hankel transformation table ]
|
|
v |
|
|
|
> |
|
|
|
0 |
|
|
|
0 |
|
|
|
> |
|
|
|
> |
|
|
|
0 |
|
|
|
0 |
|
|
|
1 |
|
|
|
1 |
|
|
|
1 |
|
|
|
0 |
|
|
|
0 |
|
|
|
1 |
|
|
|
0 |
|
[ Finite Hankel transform and its inversion formula ]
The finite Hankel transform of
where pi is a root of the equation .
The inversion formula of the finite Hankel transform is:
where is the sum of all positive roots of the equation .
[ Finite Hankel transformation table ]
where is the sum of all positive roots of the equation .
|
|
v |
|
|
|
> |
|
|
c |
0 |
|
|
|
0 |
|
|
|
> |
|
|
|
0 |
|
