§ 2 Orthogonal polynomials
1.
Legendre polynomial
[ Generating function of Legendre polynomial ]
is expanded by function press :![]()
![]()
![]()
![]()
![]()
to define the sequence of Legendre polynomials![]()
The function is called a generating or generating function .![]()
![]()
[ Expression of Legendre polynomial ]
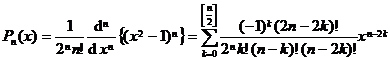
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
![]() (Merfeit expression)
(Merfeit expression)
![]()
![]()
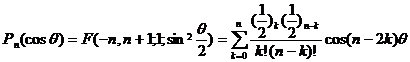
[ Legendre differential equations ]
![]()
[ Orthogonality of Legendre Polynomials ]

[ Inequalities and Special Values ]
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
[ Recursion formula and derivative formula ]
![]() (recursion relationship)
(recursion relationship)
![]()
![]()
![]()
![]()
2.
Chebyshev polynomials of the first kind
[ Generating function of Chebyshev polynomials of the first kind ] is expanded by the generating function :![]()
![]()
![]()
![]()
![]()
to define a sequence of Chebyshev polynomials of the first kind .![]()
[ Expressions for Chebyshev polynomials of the first kind ]
![]()
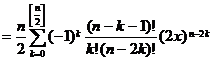
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
[ Chebyshev differential equations of the first kind ]
![]()
[ Orthogonality of Chebyshev Polynomials of the First Kind ]
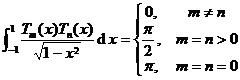
[ Inequalities and Special Values ]
![]()
![]()
![]()
[ Recursion formula and derivative formula ]
![]() (recursive formula)
(recursive formula)
![]()
![]()
![]()
3.
Chebyshev polynomials of the second kind
[ Generating function of Chebyshev polynomials of the second kind ]
is expanded by the generating function :![]()
![]()
![]()
![]()
![]()
to define a sequence of Chebyshev polynomials of the second kind .![]()
[ Expressions for Chebyshev polynomials of the second kind ]
![]()
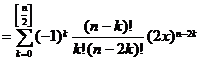
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
……………………
[ Chebyshev differential equations of the second kind ]
![]()
[ Orthogonality of Chebyshev Polynomials of the Second Kind ]

[ Inequalities and Special Values ]
![]()
![]()
![]()
![]()
[ Recursive formula and related formulas ]
![]() (recursive formula)
(recursive formula)
![]()
![]()
![]()
![]()
4.
Laguerre polynomials
1.
General Laguerre polynomials
[ Generic function of a general Laguerre polynomial ]
is expanded by the generating function :![]()
![]()
![]()
![]()
to define a general sequence of Laguerre polynomials .![]()
[ Expression of general Laguerre polynomial ]
![]()
![]()
![]()
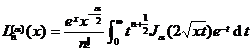
![]()
![]()
![]()
where is the Kummer function, which is a first-order Bessel function. very![]()
![]()
![]()
![]()
[ General Laguerre Differential Equations ]
![]()
[ Orthogonality of General Laguerre Polynomials ]
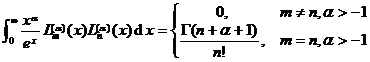
[ Inequalities and Special Values ]
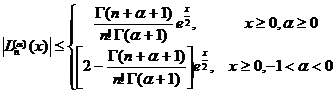
![]()
[ Recursive formula and related formulas ]
![]() (recursive formula)
(recursive formula)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
where is the Hermitian polynomial.![]()
2.
Laguerre polynomials
In general Laguerre polynomials, then , define![]()
![]()
is the Laguerre polynomial . Its corresponding formula is
![]() (generating function expansion)
(generating function expansion)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
![]() (Laguerre differential equations)
(Laguerre differential equations)
![]() (orthogonality)
(orthogonality)
![]()
![]()
![]() (recursive formula)
(recursive formula)
5.
Hermitian polynomials
[ Generating function of Hermitian polynomial ]
is expanded by the generating function :![]()
![]()
![]()
![]()
to define a sequence of Hermitian polynomials .![]()
[ Expression of Hermitian polynomial ]
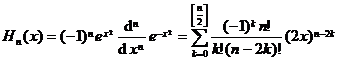
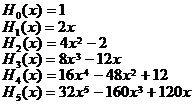
・・・・・・・・・・
![]()
![]()
where is the Kummer function .![]()
![]()
[ Asymptotic expressions for Hermitian polynomials ]
![]()
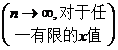
![]()
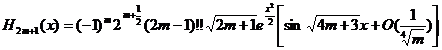
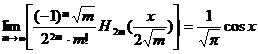
![]()
[ Hermitian differential equations ]
![]()
[ Orthogonality of Hermitian Polynomials ]
![]()
[ Inequalities and Special Values ]
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
[ Recursive formula and related formulas ]
![]() (recursive formula)
(recursive formula)
![]()
![]()
[ weighted Hermitian polynomial ] is the Hermitian polynomial of the weight function,![]()
![]()
Its expression is
![]()
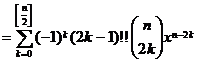
![]() relationship with
relationship with![]()
![]()
Six,
Jacobi polynomial
[ Generating function of Jacobian polynomial ]
is expanded by the generating function (where ):![]()
![]()
![]()
![]()
![]()
to define a sequence of Jacobi polynomials .![]()
[ Expression for Jacobian polynomial ]
![]()
![]()
![]()
![]()
where F is the hypergeometric function.
[ Jacobi Differential Equations ]
![]()
![]()
[ Orthogonality of Jacobian Polynomials ]
![]()
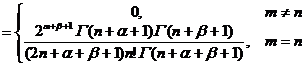
[ Inequalities and Special Values ]

where is one of the two maxima points closest to the point .![]()
![]()
![]()
![]()
[ Recursive formula and related formulas ]
![]()
![]()
![]()
(recursive formula)
![]()
7.
Geigenberger polynomial
[ Generating function of Geigenberger polynomial ] Expansion by the generating function![]()
![]()
![]()
![]()
![]()
to define the sequence of Geigenberger polynomials, also known as special spherical polynomials .![]()
[ Expression of Geigenberger polynomial ]
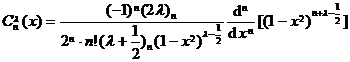

![]()
![]()
![]()
![]()
where is the hypergeometric function .![]()

······························································································ ・・・
[ Gegenberg differential equations ]
![]()
[ Orthogonality of Geigenberg Polynomials ]
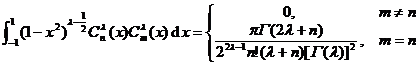
[ Inequalities and Special Values ]
![]()
![]()
![]()
![]() and not an integer)
and not an integer)![]()
![]()
( not an integer, and![]()
![]()
![]()
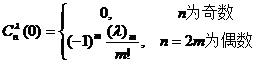
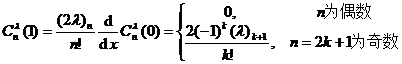
[ Recursive formula and related formulas ]
![]() (recursive formula)
(recursive formula)
![]()
![]()
![]()
![]()
![]()