§ 4 Legendre function
First,
the definition of Legendre function
[ Legendre functions of the first kind ]
![]()
![]()
It resolves single-valued in the removed plane .![]()
![]()
[ Legendre functions of the second kind ]
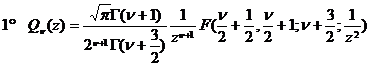
![]()
It resolves single-valued in the removed plane .![]()
![]()
![]()
![]()

![]()
It resolves single-valued in the removed plane .![]()
![]()
![]()
![]()
![]()
[ General Legendre function ]
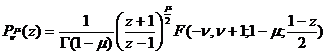
![]()
![]()

![]()
They are single-valued analytically in the removed plane and are Legendre differential equations![]()
![]()
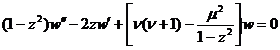
two linearly independent solutions of .
At that time , they were Legendre functions of the first and second kinds, respectively .![]()
when a positive integer), there are![]()
![]()
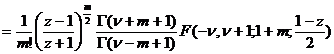
![]()
![]()
![]()
for having![]()
![]()
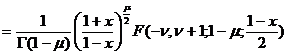
( At that time , the Legendre polynomial![]()
![]()
![]()
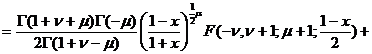
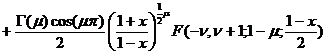
![]()
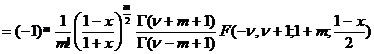
![]()
![]()
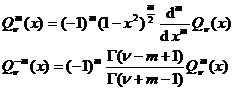
![]()
2.
Other expressions of Legendre function

![]()
![]()
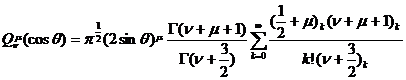
![]()
![]()
|
|
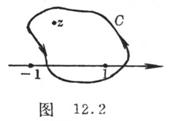
![]()
where is a forward simple closed curve on the plane (Fig. 12.2 ), the enclosing point is the sum , but not the enclosing point .![]()
![]()
![]()
![]()
![]()
When (or when an integer),![]()
![]()
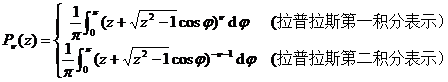
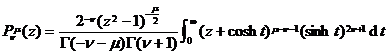
![]()
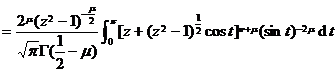
![]()
![]()
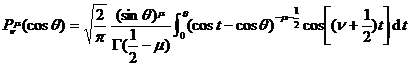
![]()
![]()
|
|
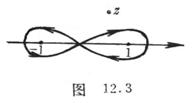
![]()
The integral route is shown in Figure 12.3. At that time ,![]()
![]()
![]()
![]()
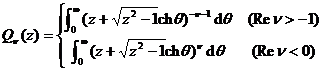
![]()
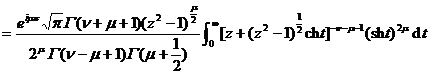
![]()
![]()
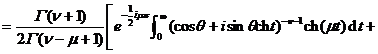

![]()
3.
The recurrence formula and related formulas of the Legendre function
![]()
![]()
![]()
![]()
![]()
![]()
![]()
The above formula is also applicable to , just replace P in the formula with . Use![]()
![]()
![]()
The corresponding recursive formula on the interval can be obtained , and there are similar formulas for .![]()
![]()
4.
Orthogonality of Legendre functions
Only the orthogonality of the function is a positive integer, and the formula is as follows![]()
![]()
![]()
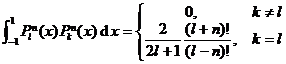
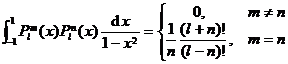
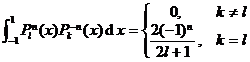
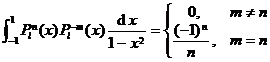
5.
Asymptotic expressions and inequalities of Legendre functions
[ asymptotic expression ]
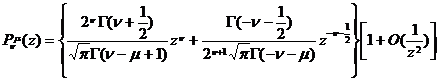
![]()
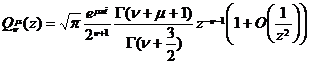
![]()
[ inequality ]
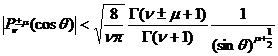
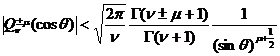
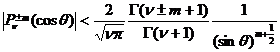
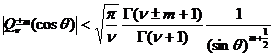
The inequalities are real numbers and positive integers .![]()
![]()