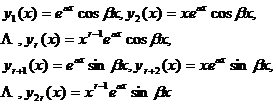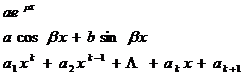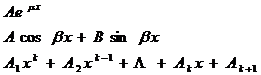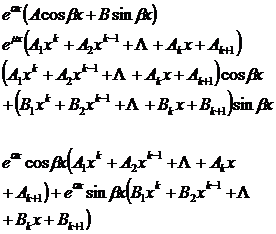§ 3 Linear Differential Equations

 

1. General Concept

 

    [ Homogeneous Linear Differential Equation and Inhomogeneous Linear Differential Equation ]   Let the differential equation

         (1)

If the unknown function in the equation and its derivatives are first-order, this kind of equation is called a linear differential equation . Because , ( 1 ) is called an n -order linear differential equation . When , (1) is called a homogeneous linear differential Equation . When , (1) is called an inhomogeneous linear differential equation . If both are constants, (1) is called a constant coefficient linear differential equation .

[ Theorem of Existence and Uniqueness of Solutions ]   If the sum is continuous in the interval , and , then for any given initial condition

Equation (1) has a unique solution , where it is a real number .

    [ Linear dependence of functions ]   For a set of functions , if there are constants that are not all zero , make the equation

If it is established on the interval , then the set of functions is said to be linearly dependent on the interval . Otherwise, the set of functions is said to be linearly independent (linearly independent) .

    [ Lonsky determinant ]   If it is a sub-differentiable function, it is called a determinant

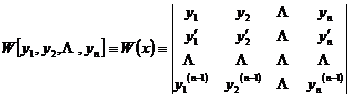
is the Lansky determinant of the function .

    The Lansky determinant has the following properties:

    1 ^o If the functions are  linearly related, then their Ronsky determinant

2 ^o If the functions  are solutions of a homogeneous linear differential equation, then the necessary and sufficient condition for their linear correlation is their Ronsky determinant

    [ The structure of the solution of the n -order homogeneous linear differential equation ]   If the homogeneous linear differential equation of order

,  

There is a linearly independent solution . Then its general solution is the linear combination of this solution, namely

where is an arbitrary constant . At this time, it is also called a set of fundamental solutions of the given homogeneous linear differential equation .

    [ Structure of solutions of inhomogeneous linear differential equations of order ]   The general solution of an inhomogeneous linear differential equation is the sum of one of its particular solutions and the general solution of the corresponding homogeneous equation, namely

where is an arbitrary constant .

 

2. Linear Differential Equations with Constant Coefficients

 

    1. How to find general solutions of homogeneous linear differential equations 

    [ Characteristic Equations and Characteristic Roots ] For homogeneous linear differential equations with real coefficients of order 

                  (2)

make the corresponding sub-algebraic equation

                    (3)

It is called the characteristic equation of the differential equation ( 2 ), and the roots of the characteristic equation (3) are called the characteristic roots of the corresponding differential equation (2) .

[ General Solution of Homogeneous Equation ]   In order to find the general solution of the homogeneous linear differential equation (2) with order constant coefficients , we only need to find its linearly independent special solutions . The corresponding linearly independent special solution is obtained .

 

characteristic root	The corresponding linearly independent special solution
( j = 1,2, … , n ) are distinct real roots	y j ( x ) = ( j = 1,2, … , n )
is a single root of the characteristic equation, then is also a single root of the characteristic equation	y 1 ( x ) = cos β x y 2 ( x ) = sin β x
is the r -fold real root of the characteristic equation	y 1 ( x ) = , y 2 ( x ) = x , …, y r ( x ) = x r -1
is the repeated root of r of the characteristic equation , then is also the r repeating root

 

    2. How to find special solutions of inhomogeneous linear differential equations 

    Inhomogeneous linear differential equations of given order

Its special solution can be found in the following two ways .

    [ Constant variation method ]   Let the general solution of its corresponding homogeneous linear differential equation be

Then the inhomogeneous linear differential equation has a particular solution

where are undetermined functions whose derivatives satisfy the system of equations

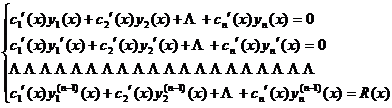
    Example of a Differential Equation 

general solution .

    The solution first finds the general solution of its corresponding homogeneous equation . 

    Because of the characteristic equation , there are characteristic roots . So the general solution of the homogeneous equation is

    Use the method of constant variation to find a particular solution y* ( x ) of an inhomogeneous equation . Let

And c ₁ ( x ), c _​​2 ( x ) are determined by the following equations

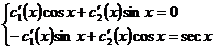
Solve the system of equations to get

after points

( k ₁ , k ₂ are arbitrary constants)

(because there is only one special solution, k ₁ = k ₂ =0 can be set ) , so the general solution of the original equation is

[ Undetermined coefficient method ] For special types , the undetermined expression of the specific solution and its corresponding derivatives of each order can be substituted into the original differential equation, and then the coefficients of similar terms are compared, and the coefficients contained in the determined undetermined expression can be obtained. Get the special solution of the equation . Now list the special solution form in some cases as follows: 

 

R ( x ) type	Pending expression for particular solution y * ( x )

 

    The table is a known constant; it is a positive integer, if the degrees of the two polynomials are different, the one with the larger degree is taken; it is an undetermined constant .

    The expressions in the right column of the table are respectively (from top to bottom) the undetermined expressions of the particular solution in the case that they are not their characteristic roots ; if they are the repeated roots of the characteristic equation, then multiply the expressions in the table by .

    Example Solving Differential Equations 

    The solution first finds the general solution of the corresponding homogeneous linear equation y ⁽⁴⁾ +2 y"+y= 0 . 

    From the characteristic equation ⁴ +2 ² +1=( ² +1) ² =0 , it can be known that the characteristic root = i is a double root . So the general solution of the homogeneous equation is

y ( x )= c ₁ cos x + c ₂ sin x+c ₃ x cos x+c ₄ x sin x

    Use the undetermined coefficient method to find a particular solution of the inhomogeneous linear equation . Since R ( x )=sin2 x , it belongs to the second type of expression ( a= 0, b= 1, = 2) in the table , and i = 2 i is not a characteristic root, so the special solution should be y* ( x )= A cos2 x + B sin2 x . Substitute into the original equation and compare the coefficients of similar terms to get

So the special solution is                       

The general solution of the original equation is

where c ₁ , c ₂ , c ₃ , c ₄ are arbitrary constants .

 

3.   Euler equation

 

    have shape

   ( is a constant )

The equation is called Euler's equation .

    Euler's equations can be replaced by variables or transformed into linear differential equations with constant coefficients of unknown functions with respect to new independent variables .

    Example Solving Euler's Equation 

    Solving for or t = ln x , the original equation becomes 

    The characteristic equation is

is a double root . The general solution is

y=e ^{- t} ( c ₁ + c ₂ t )

So the general solution of the original equation is

 

Fourth, the power series solution of homogeneous linear differential equations 

 

    [ Solution in the form of a power series ]   For general homogeneous linear differential equations with variable coefficients, it may not be possible to find a solution expressed by an elementary function, and in this case, a solution in the form of a power series can be considered .

Now take the second-order homogeneous linear differential equation as an example to illustrate the solution method (the same applies to higher-order equations ) .

where the sum can be developed into a power series . The solution of the equation in the vicinity is required, as long as the solution is first assumed to have the form of a power series

Then, the required derivatives of each order are formally calculated, and then substituted into the original equation to become the identity, and the undetermined coefficients are determined to obtain the desired power series solution .

    If it can not be developed into a power series, such as a rational fraction of x , and the denominator is equal to zero, then you can try to obtain a generalized power series form

, where a and are both undetermined constants .

    [ Solving the Legendre Equation ] Equation 

is called the Legendre equation, and its solution is called the Legendre function .

    Near x = 0 , the coefficients of the equation can be developed into power series, let

Substituting into the original equation, two linearly independent solutions can be determined

So the general solution of Legendre equation is

where A and B are arbitrary constants and are Gaussian hypergeometric series .

    If n is an integer, one of and is a polynomial, and the other is still an infinite series . Choose any constants A, B appropriately , so that when x = 1 , the value of the polynomial is 1. This polynomial is called Legendre polynomial , denoted as , it belongs to the first kind of Legendre function . The other is independent of linearity, it is an infinite series, denoted as , belongs to the second kind of Legendre function . At this time, the general solution of the Legendre equation is

where A and B are arbitrary constants .

    [ Solving the Bessel Equation ] Equation 

It is called the v -order Bessel equation, where v is any real number (or complex number), and its solution is called the Bessel function .

    Due to the coefficients of the equation , a power series cannot be formed at x = 0 , but a rational fraction of x . Let

Substitute into the original equation, make the coefficients of each power of x equal to zero, then , take =v first , and get

so

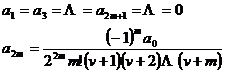
Take , a particular solution of Bessel's equation is obtained, denoted as

It is called a Bessel function of the first kind of order v .

    get another special solution

    When v is not an integer, the two special solutions are linearly independent, and the general solution of the Bessel equation is

where A and B are arbitrary constants .

    When v=n is an integer, it is linearly related . At this time, record

It is also a solution of the Bessel equation and has nothing to do with linearity . It is called the second-order Bessel function of the nth order . So the general solution of the Bessel equation is

where A and B are arbitrary constants .