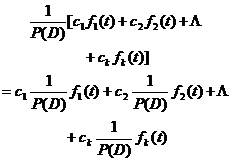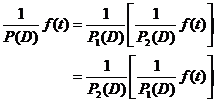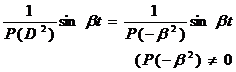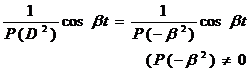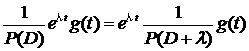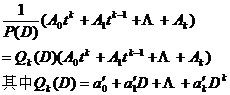§ 4
Higher order differential equations and systems of differential equations
1.
Interchange between higher-order differential equations and systems of differential equations
An equation of order n has been given
![]()
Let y 1 = y , y 2 = y' , y 3 = y" , … , y n = y ( n -1) , then solving the above n -order differential equation is equivalent to solving the following n first-order differential equations Group
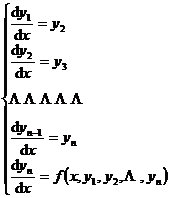
In the formula, y 1 , y 2 , … , y n are regarded as n unknown functions of the independent variable x .
Conversely, in many cases, a system of equations given n first-order differential equations can also be reduced to an n -order differential equation . For example, a system of two first-order differential equations
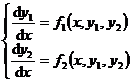 (1)
(1)
Derivative Equation (1) with respect to x
![]()
Referred to as
![]() (2)
(2)
Solve for y 2 from equation (1)
![]()
Substituting into the right-hand side of equation (2) yields a second-order differential equation
![]()
The function here is determined by the functions f 1 , f 2 , so it is known . So two first-order differential equations can be transformed into a second-order differential equation .![]()
2. Several integrable types of higher-order differential equations and their solutions
1. y ( n ) = f ( x )
write the equation as
![]()
get after points
![]()
Repeat this process to integrate n times to get the general solution of the differential equation:
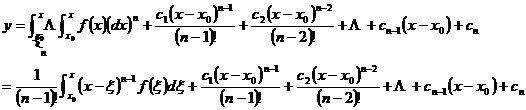
2. F ( x , y ( n ) )=0
1 ° If y ( n ) can be solved , the equation can be solved as type 1 .
2 ° If y ( n ) cannot be solved , or the expression is too complicated after solving, try to solve it in parametric form:
Let the function ( t ), ( t ) ( <t< ) satisfy
F ( ( t ),( t ))≡0
Then the original equation can be written in parametric form
x = ( t ), y ( n ) = ( t )
by
d y ( n -1) = y ( n ) d x = ( t ) ' ( t )d t
have to
![]()
And by d y ( n -2) = y ( n -1) d x = 1 ( t , c 1 ) ' ( t )d t
have to
![]()
Finally, the general solution of the parametric form of the original equation is obtained
![]()
3. F ( y ( n -1) , y ( n ) )=0
1 ° If y ( n ) can be solved from the equation :
y ( n ) = f ( y ( n - 1) )
Then let y ( n - 1) = z , the above formula becomes
![]()
This is the variable separable equation, which is solved as
z= ( x ,c 1 )
Then turn it into type 1
y ( n-1) =( x,c 1 )
Its general solution is
![]()
2 ° If y ( n ) cannot be solved , but the original equation can be written in parametric form:
y ( n -1) =( t ), y ( n ) = ( t )
Then from
d y ( n -1) = y ( n ) d x
have to
![]()
According to the method of type 2 , the general solution (parametric form) can be obtained
![]()
4. F ( y ( n -2) , y ( n ) )=0
Let the equation solve for y ( n ) :
y ( n ) = f ( y ( n -2) )
Let z=y (n-2) , multiply both sides of the equation by 2 z' to form
d( z' 2 )=2 f ( z )d z
after points
![]()
using the separation of variables method
z= ( x , c 1 , c 2 )
Then y ( n -2) = ( x , c 1, c 2 )
Integrate n -2 times to get the general solution of the original equation .
3. System of
Linear Differential Equations
1. Homogeneous linear differential equations and inhomogeneous linear differential equations
The general form of a system of [ homogeneous and inhomogeneous ] linear differential equations is
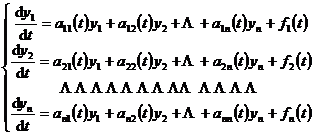 (1)
(1)
where a ik ( t ) and f i ( t ) ( ) are both ![]() known continuous functions of the independent variable t . If at least one f i ( t ) is not equal to zero, then (1) is called an inhomogeneous linear differential System of equations . If all f i ( t ) are equal to zero, then (1) is called a system of homogeneous linear differential equations, and its general form is
known continuous functions of the independent variable t . If at least one f i ( t ) is not equal to zero, then (1) is called an inhomogeneous linear differential System of equations . If all f i ( t ) are equal to zero, then (1) is called a system of homogeneous linear differential equations, and its general form is
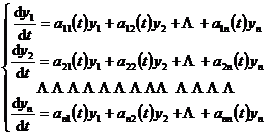 (2)
(2)
If the system of homogeneous linear differential equations (2) and the system of inhomogeneous linear differential equations (1) have the same coefficients (that is, the corresponding a ik ( t ) are the same), then (2) is said to be a system of inhomogeneous linear differential equations The corresponding homogeneous linear differential equations of (1) .
[ Theorem of Existence of Solutions ] If all the coefficients a ik ( t ) of the system of linear differential equations (1) and the right-hand side function f i ( t ) are continuous in the interval ( t 1 , t 2 ) , then the system of equations (1) is here Every point t 0 ( t 1 < t 0 < t 2 ) of the interval has a unique solution that satisfies the initial conditions ( t 0 , y 1 (0) , … , y n (0) ) , and this solution is defined in the entire interval ( t 1 , t 2 ) . _
[ Basic structure of the solution ]
A linear combination of any two solutions of a system of 1 ° homogeneous linear differential equations is also a solution of this system of equations .
2 ° The general solution of a system of homogeneous linear differential equations with n unknown functions can be expressed as a linear combination of its n linearly independent solutions .
3 ° The general solution of a system of inhomogeneous linear differential equations with n unknown functions can be expressed as the sum of one of its particular solutions and its corresponding general solution of the system of homogeneous linear differential equations .
2. System of linear differential equations with constant coefficients
system of differential equations
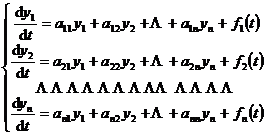 (3)
(3)
It is called a system of linear differential equations with constant coefficients, where a ij is a constant . When f i ( t ) ≡ 0 ( i =1,2, … , n ) , (3) is said to be homogeneous, when f i ( t ) ) are not always equal to zero, and (3) is said to be inhomogeneous .
[ Eigenvalues and Linearly Independent Solutions of Homogeneous Equations ]
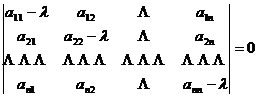
is the nth degree algebraic equation of λ , which is called the characteristic equation of the homogeneous linear differential equation system corresponding to the inhomogeneous linear differential equation system (3) , and the root of the characteristic equation is called the characteristic root .
Different forms of linearly independent solutions of homogeneous linear differential equations are given according to different situations of characteristic roots .
|
Characteristic root λ |
The form of the corresponding solution in the linearly independent solution |
Description |
|
λ is a single real root |
|
A j is an undetermined constant |
|
λ is the real root of r |
|
P j ( t ) is a polynomial with undetermined coefficients up to r -1 degree |
|
λ = α ± i β is the k repeating root |
( j = 1, 2, … ,n
) |
Q j ( t ) , R j ( t ) are polynomials whose coefficients are undetermined degree k -1 or less |
[ Use the method of constant variation to find the specific solution of the inhomogeneous system of equations ] A particular solution of the system of inhomogeneous linear differential equations (3) can be obtained from the general solution of the corresponding homogeneous system of linear differential equations by the method of constant variation .
Let y 11 , y 21, … , y n 1 ; y 12 , y 22 , … , y n 2 ; … ; y 1 n , y 2 n , … , y nn be n of the corresponding system of homogeneous linear differential equations linearly independent solutions . Then a particular solution y 1 *, y 2 *, … , y n * of the inhomogeneous system of linear equations can be determined by the following form
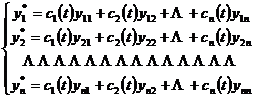
where c i ( t ) are undetermined functions that satisfy the following equations:
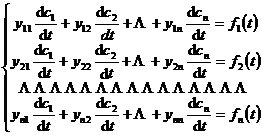
Solve from the above equations , and then integrate to get the required ci ( t ) ( i = 1,2, … , n )![]()
Example to solve a system of differential equations:
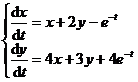 (1)
(1)
Solve the corresponding system of homogeneous linear differential equations first
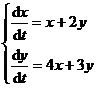 (2)
(2)
The general solution of . By the characteristic equation
![]()
It can be seen that the characteristic root is λ = 5, . ![]() Then the corresponding linearly independent solution is of the following form:
Then the corresponding linearly independent solution is of the following form:
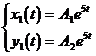
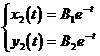
Substitute into the homogeneous linear equations (2) respectively , and use the undetermined coefficient method to determine
A 1 = c 1 , A 2 =2 c 1 , ( c 1
is an arbitrary constant)
B 1 = c 2 , B 2 = , ![]() ( c 2
is an arbitrary constant)
( c 2
is an arbitrary constant)
So the general solution of the system of homogeneous linear equations
(2) is
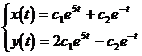 ( c 1 , c 2 are arbitrary constants)
( c 1 , c 2 are arbitrary constants)
Secondly, use the constant variation method to find a special solution of the inhomogeneous linear equation system (1) . Consider c 1
, c 2 as a function of t , and solve the following equation system
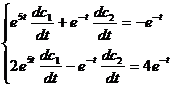
have to
![]()
After scoring, take
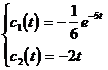
So the general solution of the system of equations (1) is
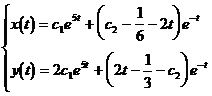
where c 1
, c 2 are arbitrary constants .
Fourth, the operator solution method of constant coefficient inhomogeneous linear differential equation and the operator solution method of equation system (elimination method)
[ differential operator and inverse operator ]
![]()
称D,D2,…,Dn为微分算子.一般地引进微分算子![]() (a1,a2,…,
(a1,a2,…,
an是常数)规定它的意义是
![]()
还引进微分算子的逆算子,Dk的逆算子记为![]() ,规定它的意义是
,规定它的意义是
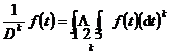 (k为正整数)
(k为正整数)
P(D)的逆算子记为![]() ,它满足条件
,它满足条件
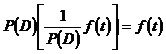
注意,![]() 的结果不是唯一的,而是一族函数.
的结果不是唯一的,而是一族函数.
[微分算子的简单性质与运算公式]
|
微分算子 |
逆算子 |
|
1o 若c1,c2,…ck为常数,则 P(D)[c1f1(t)+ c2f2(t)+…
+ ckfk(t)] =c1P(D)f1(t)+ c2P(D)f2(t)+…
+ ckP(D)fk(t)
(线性) 2o 若P(D)= P1(D)·P2(D),则 P(D)f(t) = P1(D)[P2(D)f(t)] = P2(D)[P1(D)f(t)]
(交换律) 3o P(D)eλt = eλtP(λ) 4o 微分算子 |
若c1,c2,…ck为常数,则
(线性) 若P(D)= P1(D)·P2(D),则
(交换律)
(P(λ)≠0)
逆算子 |
|
5o 6o (位移定理) 7o |
(位移定理) 设
按以下方法求得: Divide P ( D ) ( arranged according to the ascending power of D ), remove 1 according to the general polynomial division rules , and obtain the quotient in the k + 1th step . When the k - th polynomial is obtained in the quotient , the division stops . Q k ( D ). |
The meanings of the equations in the left column of the above table are usual, while the meanings of the equations in the right column are that the function families on both sides of the equal sign are the same .
[ Finding the Special Solution of Inhomogeneous Linear Differential Equation with Constant Coefficients Using the Operator Solution Method ]
1 ° equation P ( D ) x=f k ( t ) , where f k ( t ) is a polynomial of degree k in t .
There are two situations:
( i ) P (0) ≠ 0. According to the above formula 7 °
![]()
(ii) P ( 0)=0. At this time , P ( D ) = Q ( D ) D r (integer r ≥ 1 ), and Q (0) ≠ 0. According to formula 2 ° in the above table, we have
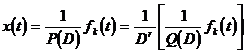
set , then![]()
![]()
2 ° equation ( when f k ( t ) is constant P ( λ ) ) . ![]()
![]()
According to the formula 6 ° in the above table , a special solution is
![]()
3 ° equation P ( D ) x = cos tf k ( t ) or P ( D ) x =sin tf k ( t ).
Consider auxiliary equations
![]()
It is of the same type as equation 2 ° , and a particular solution of it is
![]()
then the equation
![]()
There is a special solution
x ( t ) = x 1 ( t )
while the equation
![]()
There is a special solution
x ( t ) = x 2 ( t )
4 ° Equation P ( D 2 ) x = or P ( D 2 ) x = . ![]()
![]()
If P ( ) ![]() ≠ 0 , then from the formulas 4 ° and 5 ° in the above table, we can get
≠ 0 , then from the formulas 4 ° and 5 ° in the above table, we can get
![]()
or
![]()
If P ( )=0, ![]() then there are positive integer r and polynomial Q ( Q ( )
then there are positive integer r and polynomial Q ( Q ( ) ![]() ≠ 0) such that
≠ 0) such that
![]()
It can be processed according to the method of equation 1 °
(ii) .
[ Use the operator solution method (elimination method) to find the solution of the linear differential equation system ] The elimination method is one of the effective methods to solve the algebraic equation system . After the introduction of the differential operator , it is also suitable for solving the linear differential equation system . Explain this method .![]()
Let the system of linear differential equations be given
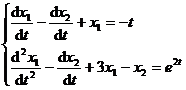
Applying the differential operator, the above system of equations can be written as

Consider this system of equations as a system of algebraic equations of two unknowns x 1 , x 2. Using the elimination method, solve x 1 , x 2 in turn .
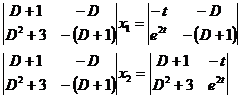
which is
![]()
Solve (1') first, and first find its corresponding homogeneous equation
![]()
The general solution of . The characteristic root is
λ 1 =1, λ 2 = i , λ 3 =![]()
So the general solution of the homogeneous equation is
![]() (
( ![]() is an arbitrary constant )
is an arbitrary constant )
Then use the operator solution method to find a special solution of equation (1')
![]()
From the previous table formula 7 ° have
![]()
From the previous table formula 3 ° have
![]()
get the particular solution of equation (1')
![]()
Finally, the general solution of equation (1') is obtained
![]()
To find x 2 ( t ) , subtract (2) from (1 ) to get
![]()
Substitute in x 1 ( t ) to get
![]()