§2 一阶偏微分方程

 

一、        柯西-柯娃列夫斯卡娅定理

 

    [一阶偏微分方程的通解]  一阶偏微分方程的一般形式Û是

或

，其中

如解出p₁，可得：

p₁ = f (x₁ , x₂ ,…, x_n , u , p₂ ,…, p_n )

    当方程的解包含某些“任意元素”(指函数)，如果适当选取“任意元素”时，可得方程的任意解(某些“奇异解”除外)，则称这样的解为通解.

    在偏微分方程的研究中，重点在于确定方程在一些附加条件(即定解条件)下的解，而不在于求通解.

    [一阶方程的柯西问题]

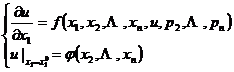
称为柯西问题，式中为已知函数，对柯西问题有如下的存在惟一性定理.

    [柯西－柯娃列夫斯卡娅定理]    设 f ( x₁ , x₂ x_n , u , p₂  p_n ) 在点 ( x₁⁰ , x₂⁰  x_n⁰ , u⁰ , p₂⁰  p_n⁰ ) 的某一邻域内解析，而在点( x₂⁰ x_n⁰ ) 的某邻域内解析，则柯西问题在点 ( x₁⁰  x_n⁰ ) 的某一邻域内存在着惟一的解析解.

    这个定理应用的局限性较大，因它要求f及初始条件都是解析函数，一般的定解问题未必能满足这种条件.

    对高阶方程也有类似定理.

 

二、        一阶线性方程

 

    1．      一阶齐次线性方程

    [特征方程 特征曲线 初积分(首次积分)]  给定一阶齐次线性方程

                  (1)

式中a_i为连续可微函数，在所考虑的区域内的每一点不同时为零(下同).方程组

      ( i = 1,2n )          

或

             (2)

称为一阶齐次线性偏微分方程的特征方程.如果曲线l: x_i = x_i (t) ( i=1,2n )满足特征方程(2)，就称曲线l为一阶齐次线性方程的特征曲线.

    如果函数 ( x₁ , x₂ x_n )在特征曲线上等于常数，即

( x₁(t) , x₂(t)  x_n(t) ) = c

就称函数 ( x₁, x₂ x_n )为特征方程(2)的初积分(首次积分).

    [齐次方程的通解]

    1^o  连续可微函数u = ( x₁, x₂ x_n ) 是齐次线性方程(1)的解的充分必要条件是： ( x₁, x₂ x_n )是这个方程的特征方程的初积分.

    2^o  设_i ( x₁ , x₂  x_n )  ( i = 1,2 n) 是特征方程(2)在区域D上连续可微而且相互独立的初积分(因此在D内的每一点，矩阵

的秩为n) ，则

u = ( ₁ ( x₁ , x₂  x_n )  _n-1 ( x₁ , x₂  x_n ) )

是一阶齐次线性方程(1)的通解，其中为n个变量的任意连续可微函数.

    [柯西问题]  考虑方程的柯西问题

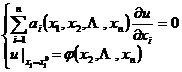
式中 ( x₂  x_n )为已知的连续可微函数.

    设_i ( x₁ , x₂  x_n )  ( i = 1,2 n) 为特征方程的任意n个相互独立的初积分，引入参变量  ()，从方程组

解出x₂  x_n 得

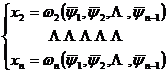
则柯西问题的解为

u = ( ₂ ( ₁ , _{2  n-1} )  _n ( ₁ , _{2  n-1} ) )

    2．      非齐次线性方程

    它的求解方法与拟线性方程相同.

 

三、        一阶拟线性方程

 

    一阶拟线性方程为

其中a_i及R为x₁ , x₂  x_n , u的连续可微函数且不同时为零.

    [一阶拟线性方程的求解和它的特征方程]

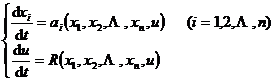
或

为原拟线性方程的特征方程.如果曲线l: x_i = x_i (t) ( i=1,2n ) , u = u(t) 满足特征方程，则称它为拟线性方程的特征曲线.

    设 _i ( x₁ x_n,u )  ( i = 1,2 n) 为特征方程的n个相互独立的初积分，那末对于任何连续可微函数，

( ₁ ( x₁ x_n , u) , ₂ ( x₁ x_n , u)  _n ( x₁ x_n , u) ) = 0

都是拟线性方程的隐式解.

    [柯西问题]  考虑方程的柯西问题

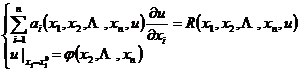
为已知的连续可微函数.

    设 ₁ ( x₁ , x₂  x_n , u)  _n ( x₁ , x₂  x_n , u) 为特征方程的n个相互独立的初积分，引入参变量 , 从

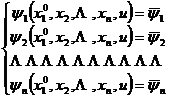
解出 x₂  x_n , u

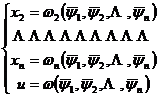
则由

给出柯西问题的隐式解.

 

四、        一阶非线性方程

 

    [完全解·通解·奇异解]  一阶非线性方程的一般形式为

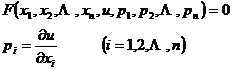
    若一阶偏微分方程的解包含任意n个独立的常数，则称这样的解为完全解(全积分).

    若V ( x₁, x₂  x_n , u , c₁ , c₂c_n ) = 0为方程的完全解，从

消去c_i ，若得一个解，则称它为方程的奇异解(奇积分).

    以两个独立变量为例说明完全解与通解、奇异解的关系，设方程

有完全解

V (x,y,z,a,b)=0          ( a,b为任意常数),

则方程等价于从方程组

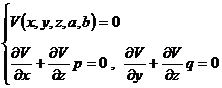
消去a,b所得的方程.

    利用常数变易法把a,b看作x, y的函数，将V (x,y,z,a,b)=0求关于x, y的偏导数，得

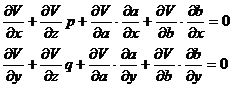
那末

与V=0联立可确定a,b.有三种情况：

    1°  ，将其与V(x,y,z,a,b)=0联立可确定不含任意常数的奇异解.

    2°  如，即回到完全解.

    3°  当时，必有，这时，如果不属于情形2° ，则a与b存在函数关系：b=(a)，这里为任意可微函数，并从方程V(x,y,z,a,b)=0和消去a,b，可确定方程的通解.

    定理  偏微分方程的任何解包含在完全解内或通解内或奇异解内.

    [特征方程·特征带·特征曲线·初积分]  在一阶非线性方程：

中，设F对所有变量的二阶偏导数存在且连续，称

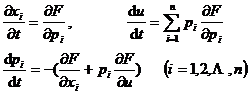
或

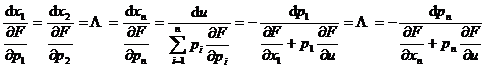
为非线性方程的特征方程.设特征方程的解为x_i=x_i(t), u=u(t), p_i=p_i(t)   (i=1,2,…,n)称它为非线性方程的特征带.在x₁,x₂x_n,u空间的曲线x_i=x_i(t), u=u(t)  (i=1,2,…,n)称为非线性方程的特征曲线.如果函数在特征方程的任一解x_i=x_i(t) (i=1,2n), u=u(t), p_i=p_i(t)   (i=1,2n)上等于常数，即

那末函数称为特征方程的初积分.

    [求完全解的拉格朗日－恰比方法]  考虑两个变量的情况.

    对于方程F(x,y,z,p,q)=0，选择使雅可比式的一个初积分G(x,y,z,p,q).解方程组

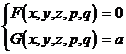     (a为任意常数)

得p(x,y,z,a)及q(x,y,z,a).则方程

dz=pdx+qdy

的通解V(x,y,z,a,b)=0(b是积分dz=pdx+qdy出现的任意常数)就是方程F(x,y,z,p,q)=0的完全解.

    例  求方程的完全解.

    解  方程的特征方程为

这里成立

所以特征方程的一个初积分为z²p² －x² .

    解方程组 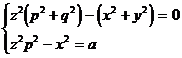                 (a为任意常数)

得                             

积分微分方程

得完全解

   (b为任意常数)

    [某些容易求完全解的方程]

    1°  仅含p,q的方程F(p,q)=0

    G=p是特征方程的一个初积分.从F(p,q)=0与p=a(a为任意常数)得q=(a)，积分

dz=adx+(a)dy

得完全解

z=ax+(a)y+b    (b为任意常数)

    2°  不显含x,y的方程F(z,p,q)=0

    特征方程为

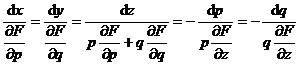
因此qdp-pdq=0，显然为一个初积分，由F(z,p,q)=0，q=pa(a为任意常数)解得p=(z,a).于是由

dz=(z,a)dx+a(z,a)dy

得

      (b为任意常数)

可确定完全解.

    3°  变量分离形式的方程

特征方程为

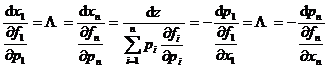
可取初积分G_i=f_i(x_i,p_i) ,  (i=1,2n).从f_i(x_i,p_i)=a_i    (i=1,2n)解出

p_i=_i(x_i,a_i)

得完全解

式中a_i,b为任意常数，且.

    [克莱罗方程]  方程

称为克莱罗方程，其完全解为

对c_i微分得

       (i=1,2,…,n)

与完全解的表达式联立消去c_i即得奇异解.

    例  求方程z－xp－yq－pq=0的完全解和奇异解.

    解  这是克莱罗方程，它的完全解是

z=ax+by+ab

    对a,b微分，得x=－b,y=－a，消去a,b得奇异解

z=－xy

    [发甫方程]  方程

P(x,y,z)dx+Q(x,y,z)dy+R(x,y,z)dz=0                                             (1)

称为发甫方程，如果P,Q,R二次连续可微并满足适当条件，那末方程可积分.如果可积分成一关系式时，则称它为完全可积.

    1°  方程完全可积的充分必要条件   当且仅当P,Q,R满足条件

                                   (2)

时，存在一个积分因子(x,y,z)，使

dU₁=(Pdx+Qdy+Rdz)

从而方程的通解为

U₁(x,y,z)=c

    特别，当时，存在一个函数U(x,y,z)满足

从而                             dU=Pdx+Qdy+Rdz

    所以方程的通解为

U(x,y,z)=c

    所以完全可积的发甫方程的通解是一单参数的曲面族.

    定理  设对于发甫方程(1)在某区域D上的完全可积条件(2)成立，则对D内任一点M(x,y,z)一定有方程的积分曲面通过，而且只有一个这样的积分曲面通过.

    2°  方程积分曲面的求法

    设完全可积条件(2)成立.为了构造积分曲面，把z看成x,y的函数(设R(x,y,z)≠0)，于是原方程化为

由此得方程组

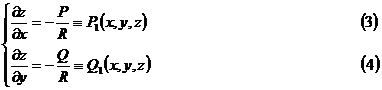
发甫方程(1)与此方程组等价.

    把方程(3)中的y看成参变量，积分后得一个含有常数的通解

然后用未知函数代替常数，将代入方程(4)，在完全可积的条件下，可得的一个常微分方程，其通解为

c为任意常数，代回中即得发甫方程的积分曲面

z=(x,y,(y,c))

    由于发甫方程关于x,y,z的对称性，在上面的讨论中，也可把x或y看成未知函数，得到同样的结果.

    例  求方程yzdx+2xzdy+xydz=0的积分曲面族.

    解  容易验证完全可积条件成立，显然存在一个积分因子，用它乘原方程得

积分后得积分曲面族

xy²z=c

    也可把方程化为等价的方程组

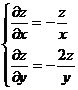
把y看成参变量，积分得通解

用未知函数代替，将代入方程得

积分后有

所以原方程的积分曲面族是

xy²z=c

 

五、        一阶线性微分方程组

 

    [一阶线性偏微分方程组的一般形式]  两个自变量的一阶线性方程组的形式是

或

                               (1)

其中A_ij,B_ij,C_ij,F_i,a_ij,b_ij,f_i是(x,t)的充分光滑函数.

    [特征方程·特征方向·特征曲线]

称为方程组(1)的特征方程.在点(x,t)满足特征方程的方向称为该点的特征方向.如果一条曲线l，它上面的每一点的切线方向都和这点的特征方向一致，那末称曲线l为特征曲线.

    [狭义双曲型方程与椭圆型方程]  如果区域D内的每一点都存在n个不同的实的特征方向，那末称方程组在D内为狭义双曲型的.

    如果区域D内的每一点没有一个实的特征方向，那末称方程组在D内为椭圆型的.

    [狭义双曲型方程组的柯西问题]

    1°  化方程组为标准形式对角型

    因为det(a_ij-_ij)=0有n个不同的实根₁(x,t) _n(x,t)，不妨设

那末常微分方程

的积分曲线l_i  (i=1,2,…,n)就是方程组(1)的特征曲线.

    方程

的非零解(_k⁽¹⁾ _k⁽ⁿ⁾)称为对应于特征方向_k的特征矢量.

    作变换

可将方程组化为标准形式对角型

    所以狭义双曲型方程组可化为对角型，而一般的线性微分方程组(1)如在区域D内通过未知函数的实系数可逆线性变换可化为对角型的话，(此时不一定要求 _i都不相同)，就称这样的微分方程组在D内为双曲型的.

    2°  对角型方程组的柯西问题

    考虑对角型方程组的柯西问题

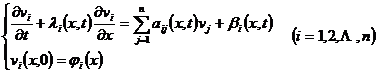
_i(x)是[a,b]上的连续可微函数.设_ij,_i,_i在区域D内连续可微，在D内可得相应的积分方程组

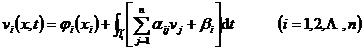
式中为第i条特征曲线l_i上点(x,t)与点(x_i,0)之间的一段，(x_i,0)为l_i与x轴上[a,b]的交点.上式可以更确切地写为

                                    (i=1,2n)

式中x_i=x_i(x°,t°,t)为过点(x°,t°)的第i条特征曲线，利用逐次逼近法可解此积分方程.为此令

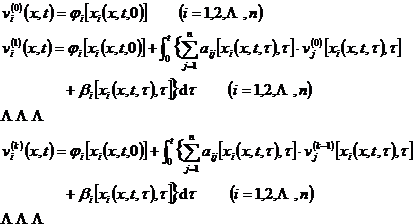
序列{v_i^(k)} (k=0,1,2)一致收敛于积分方程的连续可微解v_i(x,t)  (i=1,2n)，这个v_i(x,t)也就是对角型方程组的柯西问题的解.

    设在区域D内对角型方程组的柯西问题的解存在，那末解与初值有下面的关系：

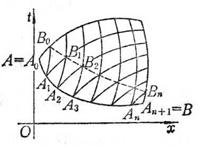
    (i)    依赖区间：过D中任意点M(x,t)作特征曲线l₁,l_n，交x轴于B,A，称区间[A,B]为M点的依赖区间(图14.1(a))，解在M点的值由区间[A,B]的初值确定而与[A,B]外的初值无关.

    (ii)   决定区域：过点A,B分别作特征曲线l_n,l₁,称l_n,l₁ 与区间[A,B]围成的区域D₁为区间[A,B]的决定区域(图14.1(b))，在区域D₁中解的值完全由[A,B]上的初值决定.

    (iii)  影响区域：过点A,B分别作特征曲线l₁,l_n，称l₁,l_n与[A,B]围成的区域D₂为区间[A,B]的影响区域(图14.1(c)).特别当区间[A,B]缩为一点A时，A点的影响区域为D₃(图14.1(d)).在区域D₂中解的值受[A,B]上的初值影响，而在区域D₂外的解的值则不受[A,B]上的初值影响.

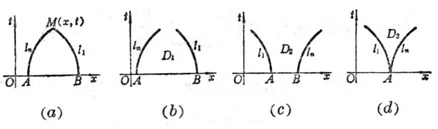
图14.1

 

    [线性双曲型方程组的边值问题]  以下列线性方程组来说明：

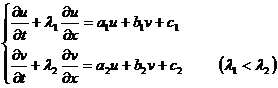                                   (1)

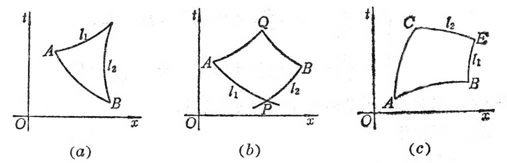
    1°  第一边值问题(广义柯西问题)  设在平面(x,t)上给定曲线段，它处处不与特征方向相切.过A,B分别引最左和最右的特征曲线l₁及l₂.要求函数u(x,t),v(x,t)在，l₁及l₂围成的闭区域上满足方程组，且在上取给定的函数值(图14.2(a)).

    2°  第二边值问题(古沙问题)  设l₁是过P点的第一族特征线，l₂是第二族特征线，在l₁的一段PA上给定v(x,t)的数值，在l₂的一段PB上给定u(x,t)的数值，过A点作第二族特征线，过B点作第一族特征线相交于Q.求在闭区域PAQB上方程组的解(图14.2(b)).

    3 ° The third boundary value problem Let AB be a non-characteristic curve arc, AC be a characteristic arc, and there is no other characteristic curve passing through point A between AB and AC , and the second family of characteristic lines passing through point C It intersects with the characteristic line of the first family passing through point B at point E. Given the value of v ( x, t ) on AC , and the value of u ( x, t ) on AB , find the closed area enclosed by ACEBA . The solution of the system of equations on region D ( Fig. 14.2( c ) ).   

                                     Figure 14.2

    [ Characteristic line method for approximate solution of boundary value problem ] The above definite solution problem can be solved by stepwise approximation method, or approximate value solved by characteristic line method . Take the first boundary value problem as an example to illustrate . 

    Take n sub-points A ₁ , A ₂ , A _n on the curve AB , and denote A as A ₀ , B as A _{n +1} , draw a straight line through A ₀ according to the second characteristic direction of A 0 and through _A 1 _according to The first characteristic direction of A ₁ is drawn as a straight line to intersect at B ₀ ; the second characteristic direction of A 1 through A 1 is drawn as a straight line and the first _{characteristic} direction _of A _{2 is drawn as a straight line through} A ₂ to intersect at B ₁ Finally, B _n is obtained ( Fig. 14.3 ). The following approximate formulas are used to determine the solution u ( x,t ), v ( x, t ) of the system of equations (1) in B _i ( i = 0,1,2, … , n ) value:  

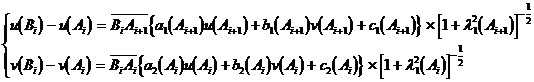
Then the values ​​of u and v are obtained at the nodes of a triangular mesh . After appropriate interpolation, when n is quite large and the distance between A _i and A _{i +1} is quite small, a sufficiently approximate solution to the proposed problem is obtained .

    [ Special form of quasi-linear equation system reducible system ] The problem of general quasi-linear equation system is more complicated  , and the results of current research are not many. The following introduces a special form of quasi-linear equation system reducible system . If the equation system

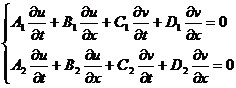
All the coefficients in is just a function of u, v , which is called a reducible system .

    Consider meeting the conditions

The solution of the system of equations u=u ( x,t ), v=v ( x,t ) . x,t can be expressed as a function of u,v , and

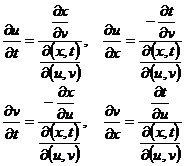
The original equation becomes

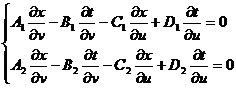
This is a linear equation system about the independent variables u, v . In this way, the solution of the quasi-linear equation system is transformed into the problem of solving the linear equation system . And the solution of the linear equation system satisfying the conditions , in ( x, t ) The image on the plane is the solution of the original quasi-linear equation system .