Chapter 15 Integral Equations
Integral equation theory is an important branch of functional analysis, and it is an important mathematical tool for studying other mathematics disciplines (such as partial differential equation boundary value problems) and various physical problems. This chapter describes the linear integral equations, focusing on the properties and solutions of the Fredholm integral equations; briefly introduces the Volterra integral equations and some singular integral equations; in addition, briefly describes the successive approximation methods and The kernel is pre-solved, and the approximate solution is illustrated with an example. Finally, a nonlinear integral equation is investigated.
§ 1 General concept of integral equation and Fredholm equation
1. General concept of integral equation
1. Definition and classification of integral equations
[ Linear integral equation ] Equation containing unknown function y ( x ) under integral sign
(1)
called the integral equation. where α ( x ), F ( x ) and K ( x, ξ ) are known functions, λ , a, b are constants, variables x and ξ can take all values within the interval ( a, b ) ; K ( x ) , ξ ) is called the kernel of the integral equation, F ( x ) is called the free term, and λ is called the parameter of the equation. If K ( x, ξ ) is a symmetric function with respect to x, ξ , equation (1) is said to be an integral equation with a symmetric kernel; if the unknown function in the equation is first-order, it is called a linear integral equation, equation (1) is the general form of a linear integral equation; if F (x ) ≡ 0 , then equation (1) is called a homogeneous integral equation, otherwise it is called an inhomogeneous integral equation.
[ One-dimensional Fredholm integral equation ( Fr equation) ]
Fr equations of the first kind
Fr equations of the second kind
Fr equations of the third kind
[ n -dimensional Fredholm integral equation ]
It is called the n - dimensional Fredholm integral equation, where D is the region in n -dimensional space, P,P 1 Î D , and their coordinates are ( x 1 , x 2 , L , x n ) and , a ( P )= a ( x 1 , x 2 , L , x n ), F ( P )= F ( x 1 , x 2 , L x n )
) and K ( P, P 1 ) = K ( x 1 , x 2 , L , x n , are known functions, and f ( P ) is an unknown function.
Regarding the solution of the Fr equation, the one-dimensional and n (>1) -dimensional cases are completely similar, so only the one-dimensional Fr equation will be considered in the following discussion.
[ Volterra integral equation ] If the integral upper limit b is changed to a variable upper limit, the above three types of Fr equations are called the first, second and third types of Volterra integral equations respectively.
Since the third kind of Fr equation, when a ( x ) is a positive function in ( a , b ) , can be transformed into
It is the second kind of Fr equation that contains the unknown function as the kernel of the integral equation. Therefore, this chapter focuses on the one-dimensional second kind of Fr equations.
2. Relationship between integral equations and differential equations
Some integral equations can be transformed into differential equations, and integral equations can also be derived from differential equations. First consider the initial value problem of the second-order linear differential equation:
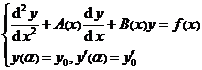( 2 )
If it is solved from equation (2) , and then x is integrated twice over the interval ( a , x ) , using the initial conditions, it is not difficult to obtain * after simple calculation ,
make
and
The above formula can be written in the following form :
(3)
This is a Volterra equation of the second kind, where the kernel K is a linear function of x .
Example 1
Initial value problem
(4)
into an integral equation
(5)
Conversely, by applying the derivation rule under the integral sign, the integral equation (3) can be transformed into the differential equation (2) by differentiating it twice . Let x = a in (3) and the result of its first derivation, and the initial conditions must be given. In Example 1 , taking the derivation of (5) , we get
(6)
Derivation one more time yields the original differential equation (4) and gives the initial conditions from equations (6) and (5)
y (0)=1, 
For boundary value problems, the method is similar, consider a simple example first.
Example 2
from the question
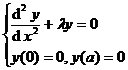
Start, integrate twice, derive the relation
From this it is immediately clear that the condition y (0)=0 holds. Determine C from the second endpoint condition y ( a )=0 :
So there is a relation
(7)
make
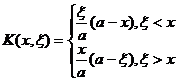
Then equation (7) becomes
(8)
This is the Fr equation of the second kind. To go from this integral equation back to the differential equation, simply take the derivative of equation (8) twice, and we get
In the integral equation (7) , let x = 0 and x = a , the boundary value condition y (0)= y ( a )=0 can be directly deduced .
Note: In this example,
1° is discontinuous at x = ξ and has a jump - 1 as x increases past ξ .
2° K is a linear function of x , i.e. satisfying and K equals zero at the endpoints x = 0, x = a .
3° K ( x , ξ ) = K ( ξ , x ), i.e. the kernel is symmetric.
If a similar approach is used, for the more general boundary value problem of second-order homogeneous equations with homogeneous endpoint conditions:
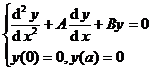
Then in addition to A = 0 , a kernel that is discontinuous at x = ξ can be obtained .
2. Green's function and its physical meaning
[ Green's function ] On the interval [ a , b ] , consider the differential equation
Ly + Φ ( x )=0
The boundary value problem of , where L is the differential operator:
Homogeneous boundary conditions are satisfied at the endpoints x = a , x = b , where α , β are constants.
In order to obtain the form of the solution to this problem, first construct a function G such that for a given number ξ ,
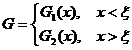
and satisfy the conditions:
(i) Functions G 1 and G 2 satisfy LG =0 in their defined interval , that is , when x < ξ , LG 1 =0; when x > ξ , LG 2 =0 .
(ii) The
function G satisfies the boundary condition, that is, G 1 satisfies the boundary condition at x = a , and G 2 satisfies the boundary condition at x = b .
(iii) The
function G is continuous at x = ξ , ie G 1 ( ξ ) = G 2 ( ξ ) .
(iv)
The derivative of G takes x = ξ as a discontinuity, and its jump is , i.e.
It can be shown that if this function G with ξ as parameter exists, the solution of the original problem has the following form:
(2)
For example , G ( x, ξ ) can be
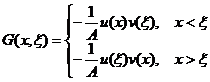(3)
where A is determined by the relation
A constant that determines, u ( x ) is a solution that satisfies the homogeneous boundary value condition given at x = a at Ly = 0 , and v ( x ) is a solution that satisfies the boundary value condition at x = b . Then G ( x, ξ ) obviously satisfies the conditions (i)~(iv) .
Furthermore, it can be shown that, for G ( x, x ) defined by (3) , the function y determined by relation (2) satisfies differential equation (1) and u ( x ) when x = a and v ( x) ) at the same homogeneous boundary conditions specified by x = b .
A function that satisfies the conditions ( i ) ~ (iv) or is defined by equation (3) is called a Green 's function associated with the differential expression Ly and the boundary conditions. In many physical problems, this function has a simple physical meaning, which is explained in the next paragraph.
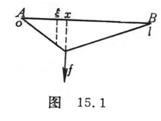[ A typical example of a linear integral equation ] Consider an elastic chord of length l , assuming that at equilibrium, the chord's position is on the line segment O1 of the Ox axis . A unit force is applied at point x , so that each point of the string gets a dispersion, the resulting dispersion at point x is denoted by G ( x, x ) (Figure 15.1 ). The function G ( x, x ) is a function of two points ( x and x ) , an external force is applied at the point x , and the dispersion is measured at the point x, and G is called the influence function.
If the two ends of the string are fixed at points A and B on the x -axis , and the tension of the string is T 0 , the string will take the shape shown in Figure 15.1 under the action of unit force applied outside the point x . According to Hooke 's law and the force equilibrium condition, at point x we have
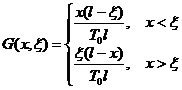
This is the influence function of the string.
From the law of conservation of energy , the reciprocity principle of G ( x , x ) can be derived: the dispersion at point x when an external force is applied at point x is equal to the dispersion at point x when a force of the same magnitude is applied at point x , which is
G ( x , x ) = G ( x , x )
If the force F exerted on the string is distributed continuously, and the linear strength is p ( x ), the force acting on a small segment of the string between the points x and x + Dx on the string is close to p ( x ) ) D x . Adding these force elements that cause the deformation of the string gives the shape of the string
1° Under the action of a certain force, the chord becomes a known shape y=y ( x ), and the distribution strength p ( x ) of the fixed force is obtained, and the first type of Fr integral equation containing the unknown function p ( x ) is obtained.
(1)
2° Let the force change with time t and the intensity at point x is
p ( x ) sin w t
( w >0)
Then the motion of the string is given by the equation
y = y ( x ) sin w t
Describe the cyclic movement.
Let r ( x ) be the linear density of the chord at the point x , then at time t , the small chord segment between the point x and x + D x is not only affected by the force p ( x ) sin w t D x , but also by the force p ( x ) sin w t D x inertial force
sin w t D x
, then equation (1) can be transformed into the following form:
(2)
in the formula
K ( x , x ) = G ( x , x ) r ( x ),
l = w 2
If the function p ( x ) is given, then F ( x ) is also given, so the integral equation (2) is the Fr equation that determines the function y ( x ) . Note that due to the definition of F ( x ) , we have
F (0)= F ( l )=0
If the density r ( x ) = r is constant, and F ( x ) has a second-order continuous derivative, then the solution to equation (2) is
which is
(3)
in the formula
Differentiating equation (3) twice, we get
On the other hand, it can be shown that any solution of this differential equation equal to 0 at x = 0 and x = 1 is a solution of the integral equation (2) .
3.
Fr equation with separable kernel (degenerate kernel)
[ Separable kernel (degenerate kernel) ] If the kernel K ( x , x ) can be decomposed into the following form:
Then K ( x , x ) is called separable kernel or degenerate kernel. It may be assumed that the n functions f k ( x ) ( k =1,2, L , n ) are linearly independent on the interval concerned.
For example, if the kernel is any polynomial with respect to x and x , then the kernel is a degenerate kernel, and the kernel sin( x+ x ) is also a degenerate kernel.
[ Solution of Fr equations of the second kind with separable kernels ] Fr equations of the second kind with separable kernels
(1)
which is
(2)
The solution is as follows, first set
( k =1,2, L , n )
but
So all solutions to the given integral equation (1) should take this form. So the problem boils down to finding the constants c 1 , c 2 , L , c n .
Multiply both sides of (2) by g i and integrate, let
,
( i = 1,2, L , n , j =1,2, L , n )
Then c 1 , c 2 , L , c n satisfy the system of equations
( i = 1,2, L , n )
which is
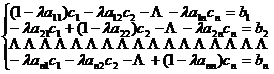( 3 )
The matrix form is
( I - l A ) c = b
where I is a unit matrix of order n , A =( a ij ), c = ( c 1 , c 2 , L , c n ) t , b = ( b 1 , b 2 , L , b n ) t . A necessary and sufficient condition for the existence of a unique solution to this system of equations is: the coefficient determinant of the equation
D = det ( I - l A ) 1 0
If F ( x ) o 0, then b i =0( i =1,2, L n ) , then equation (3) is a homogeneous system of equations. Therefore , when D 1 0 , y ( x ) o 0 is the trivial solution (zero solution) of the integral equation (1) , and is the only solution. When D = 0 , at least one c i can be arbitrarily specified, and the rest c j can be obtained, so there are infinitely many solutions to the integral equation (1) .
The values of l that make D = 0 are called eigenvalues. Any non-trivial solution of a homogeneous integral equation is called the characteristic function corresponding to the integral equation.
If for a given eigenvalue of l, r can be arbitrarily specified from the constants c 1 , c 2 , L , and c n , then r linearly independent corresponding eigenfunctions can be obtained .
If F ( x ) is not constant zero , but is orthogonal to g 1 ( x ), g 2 ( x ), L , g n ( x ) , then b i =0 ( i =1,2, L n ) . Then the system of equations (3) is still homogeneous, and the above discussion applies, unless the solution of the integral equation here also contains the function F ( x ) . Thus the trivial value c 1 = c 2 = L = c n =0 leads to the solution y = F ( x ) . The solution for an eigenvalue of l is the sum of F and any multiple of the eigenfunction.
Finally, if at least one of the b i on the right-hand side of equation ( 3 ) is not zero, when the determinant D 1 0 , there is a unique non-trivial solution to equation (3) , so the unique non-trivial solution of integral equation (1) can be obtained . Trivial solution, when D = 0 , then equation (3) is either incompatible, then the integral equation (1) has no solution; or at least two of the n equations are the same, then the integral equation (1) ) has infinitely many solutions.
Solve the Integral Equation by Example
(1)
The solution can be rewritten as
y ( x ) = l ( c 1 - 3 c 2 x ) + F ( x ) (2)
in the formula
,
The system of equations to determine c 1 , c 2 is
(3)
Its coefficient determinant is
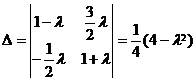
Then the condition for the existence of a unique solution to the integral equation (1) is l 1 ± 2 . Solve c 1 , c 2 from (3) and substitute into (2) to get the solution of (1) . In particular, if F ( x )=0, l 1 ± 2, then the only solution is the trivial solution y ( x )=0 . The number λ = ± 2 is the eigenvalue of the problem.
If λ = 2 , the equation system (3) is
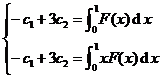
The two equations are incompatible unless the function F ( x ) satisfies the condition
In this case the two equations are the same.
If λ = - 2 , then the system of equations (3) is
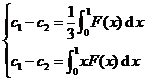
The two equations are also incompatible unless the function F ( x ) satisfies the condition
The two equations are then the same.
The solution of the integral equation (1) is now discussed in detail .
1° First consider the case of a homogeneous equation (ie, F ( x )=0 ). If l 1 ± 2 , the only solution is the trivial solution y ( x )=0 .
When λ =2 , the system of algebraic equations gives only one condition c 1 =3 c 2 . At this time, the solution is
y ( x ) = c 1 (1 - x )
where c 1 =3 λ c 2 =6 c 2 is an arbitrary constant, and 1 - x is an eigenfunction corresponding to the eigenvalue λ = 2 .
When λ = - 2 , the solution is
y ( x ) = c 2 (1 - 3 x )
where c 2 = λ c 1 = - 2 c 1 is an arbitrary constant, 1 - 3 x is the characteristic function corresponding to λ = - 2 .
Equation (2) shows that any solution to the original integral equation (1) is expressed as:
y ( x )= F ( x )+ c 3 (1 - x )+ c 4 (1 - 3 x )
In the formula , . Then it is deduced that any solution of the original integral equation (1) can be expressed by a certain linear combination of characteristic functions and the sum of F ( x ) .
2° In the inhomogeneous case (that is, F ( x ) is not always equal to zero), if l 1 ± 2 , then the integral equation (1) has a unique solution.
When λ = 2 , the integral equation (1) has no solution unless F ( x ) is orthogonal to the characteristic function 1 - x * corresponding to λ = 2 on the interval [0,1] , that is
Under this condition, using c 1 -3 c 2 = , the solution of integral equation (1) is given.
In the formula, c 1 =6 c 2 is an arbitrary constant, so there are infinitely many solutions at this time.
Similarly, when λ = - 2 , the integral equation (1) has no solution unless F ( x ) is orthogonal to 1-3 x on the interval [0,1] , i.e.
Then there are infinitely many solutions as follows:
where c 2 =-2 c 1 is an arbitrary constant.
The theory of Hilbert - Schmidt
When the kernel K ( x, ξ ) of the homogeneous Fr equation is inseparable, in particular, when K ( x, ξ ) is given by different analytical expressions for x > ξ and x < ξ , there are generally infinite eigenvalues λ n ( n = 1,2, L ), the eigenfunction corresponding to each eigenvalue is determined except for a multiplier; in exceptional cases, a given eigenvalue l k may correspond to two or more Multiple independent feature functions. This paragraph will introduce some properties of such eigenfunctions.
[ Properties of the Fr equation with a symmetric kernel ] If the value of its own is unchanged when its variables are exchanged in the real kernel, this kernel is called a symmetric kernel.
The characteristic function system of the homogeneous Fr equation with a symmetric kernel at 1° is orthogonal.
The eigenvalues of the Fr equation with a real symmetric kernel at 2° are all real numbers.
Note that the nuclear asymmetric Fr equation can have imaginary eigenvalues.
[ Hilbert - Schmidt theorem ] Let Φ be a square integrable function, then the form
The function f ( x ) of , can be obtained from the symmetric kernel homogeneous Fr equation
The linear combination expression of the characteristic functions y 1 ( x ), y 2 ( x ), L on [ a , b ] , if there are infinitely many characteristic functions, then the obtained infinite series is on the interval [ a , b ] Absolute and consistent convergence.
[ Schmidt's formula ] Consider inhomogeneous Fr equations of the second kind
where K ( x , x ) is a square-integrable symmetric kernel over the defined interval, and is assumed to be a continuous function of two variables x , ξ over the square k 0 ( a ≤ x ≤ b , a ≤ ξ ≤ b ) , F ( x ) is a known uniform continuous function, y ( x ) is an unknown function, and λ is a parameter, there is a Schmidt formula
( λ ≠ λ n , i.e. λ is not an eigenvalue) (1)
The series on the right is absolutely and uniformly convergent, where F n is determined by:
( n =1,2, L ) (2)
[ Kernel Expansion Theorem ] A symmetric kernel K ( x , x ) can be expanded into a series
For any fixed x , this series has
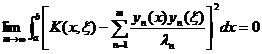
[ Integral equation with asymmetric kernel ] Let the kernel K ( x , x ) not be symmetric, but it can be expressed as
K ( x , x ) = r ( x ) G ( x , x )
In the formula, r ( x ) is continuous and invariant in ( a , b ), and G ( x , x ) is symmetric, then it has the following properties:
1 ° The two eigenfunctions ym ( x ) and yn ( x ) corresponding to different eigenvalues lm and ln are orthogonal on [ a , b ] with respect to the weight function r ( x ) , i.e.
The eigenvalues of 2° K ( x , x ) are all real numbers.
3° If there is a solution to the non-homogeneous Fr equation of the second kind, then the solution is given by (1) , and the weight function r ( x ) is used to multiply the integrand contained on both sides of the equation (2) .
[ Integral equation with Hermitian kernel ] Let the kernel K ( x , x ) be a double check, if
Then K ( x , x ) is called the Hermitian kernel, where it represents the complex conjugate function of K ( x , x ) . An integral equation with a Hermitian kernel has the following properties:
1 ° The two eigenfunctions y m ( x ) and y n ( x ) corresponding to different eigenvalues lm and ln are orthogonal in the Hermitian sense on [ a , b ] :
The eigenvalues associated with the Hermitian kernel of 2° on [ a , b ] are all real numbers.
3° Let the eigenfunctions be normalized in the Hermitian sense:
If the inhomogeneous Fr equation of the second kind has a solution, then this solution is given by (1) , and (2) is changed to
( n =1,2, L )
[ Integral equation with antisymmetric kernel ] Let K ( x , x ) satisfy the condition
K ( x , x )= - K ( x , x )
Then K ( x , x ) is called an antisymmetric kernel, and iK ( x , x ) is a Hermitian kernel. Therefore, the integral equation with an antisymmetric kernel
If l is replaced by l , then the integral equation with Hermitian kernel is obtained
It can be seen that integral equations with antisymmetric kernels must have eigenvalues, and they are all pure imaginary numbers.
[ Adjoint Kernel and Self-Adjoint Kernel ] Let u ( x ) be a eigenfunction of a double kernel K ( x , x ) ( it is not necessarily a Hermitian kernel ) corresponding to the eigenvalue l , and v ( x ) is the kernel corresponding is an eigenfunction of eigenvalue m , if , then
Here it is called the adjoint kernel of K ( x , x ) . If = K ( x , x ) , then K ( x , x ) is called a self-adjoint kernel. Obviously, the real symmetric kernel and the Hermitian kernel are both self-adjoint kernels.
5. The successive approximation method and Neumann series solution of the second kind of Fr equation
[ Successive approximation method ] In some cases, the second kind of Fr equation can be solved by successive approximation method. For this, let the equation
(1)
The solution of can be expressed as a power series of l :
y ( x ) = y 0 ( x ) + y 1 ( x ) l + y 2 ( x ) l 2 + L
(2)
If the series (2) is uniformly convergent with respect to x on the interval [ a , b ] , then substitute it into (1) , integrate item by item, and compare the coefficients of l to obtain the recursion that determines y n ( x ) formula
y 0 ( x ) = F ( x ), ( n =1,2, L ) (3)
where y n ( x ) ( n =1,2, L ) are all continuous functions. If sufficiently small, series (2) converges absolutely and uniformly with respect to x , so series (2) is a continuous function and a solution to integral equation (1) .
[ Stacked kernel × pre-solution kernel × Neumann series solution ] Let K ( x , x ) be the kernel, and the recursive formula
K 1 ( x , x ) = K ( x , x ), ( n =2,3,4, L ) (4)
The resulting K n ( x , x ) is called the n -fold kernel of the known kernel K ( x , x ) . It satisfies the following formula
where p and q are any positive integers.
Since F ( x ) and K ( x , x ) are continuous on [ a , b ] and k 0 ( a ≤ x ≤ b , a ≤ ξ ≤ b ), respectively, there are maxima m and M respectively :
, 
At that time , the series converges absolutely and uniformly within k 0 , denoted as
(5)
If y n ( x ) is expressed by the free term F ( x ), it follows from (3) , (4)
and substituting it into series (2) to get
(6)
Because the series (5) converges uniformly within k 0 , for any fixed value x on [ a , b ] , it converges uniformly with respect to x within the interval , so the solution of integral equation (1) is obtained
, (7)
The function R ( x , x ; l ) that does not depend on the free term F ( t ) in the formula is called the kernel (or the pre-solution kernel of the Fr equation), and the series (5) is called the Neumann series.
[ Existence and Uniqueness Theorem ] If the series (5) is rewritten as
From the above formula (5) , it can be transformed into
Changing the sign can be written as
Therefore, when F ( x ) in equation (1) is replaced by K ( x , y ) , the above equation shows that there is a pre-solution kernel R ( as a function of two variables x , y and parameter l ) is equation (1 ) is the only solution.
Example to illustrate the actual algorithm of the pre-solution kernel. Let the integral equation (1) be
K ( x , x )=1 - 3 x x
Its various overlapping kernels are calculated from formula (4) :
Therefore , it is easy to deduce ( n ≥ 3 ) from this , so we have
which is
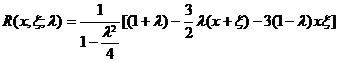
It is worth noting that this formula can give a pre-solution kernel for all λ values ( except λ = ± 2 ), but the corresponding Neumann series converge only then .
6. Fredholm's theory
[Fr square mother ] The pre-solution kernel R ( x , ξ ; λ ) can be expressed as the ratio of two power series about λ that are convergent for all λ values .
If the pre-unchecked table becomes
(1)
in the formula
(2)
(3)
Δ ( λ ) is called the Fr denominator, which is independent of the variables x , ξ . In the formula, the coefficient c n and the function D n ( x , ξ ) can be calculated successively by the following recursive formula:
L L L
then the equation
The solution of can be obtained by substituting ( 1 ) into the formula ( 7 ) in the previous paragraph , and its form is
( 4 )
This result is consistent with the solution obtained in Section 3 when K ( x , x ) is separable, and both series (2) and (3) contain only finite terms.
More generally, if the ratio of the series (2) to (3) is expressed by a power series with respect to l ( by division or otherwise ) , the result will be reduced to the series form of (6) in the previous paragraph, while it is converges only for sufficiently small values of l ; but the series expansion of the numerator and denominator of the last term in (4) converges for all values of l .
The denominator D ( l ) is equal to zero only when l takes an eigenvalue. In this case, the Fr equation either has no solution or has infinitely many solutions, and (4) no longer holds.
[ The zero point of D ( l ) and the Fr equation ] Applying the existence and uniqueness theorem, we have the following conclusions:
1° If l is not the zero point of D ( l ) , then for any F ( x ), (4) is the only solution to the Fr equation.
All zeros of the 2° function D ( l ) are the poles of the pre-solution kernel.
3° If l c is the zero of D ( l ) , then the homogeneous equation
has a non-zero solution.
So all zeros of D ( l ) are eigenvalues of the above integral equation, that is to say, the homogeneous equation
(5)
has a non-zero solution. If l is not the zero point of D ( l ) , then from 1 o , the non-homogeneous Fr equation has a unique solution to any F ( x ) , especially, the above homogeneous equation has only zero solution, namely
If l is a zero of D ( l ) , then it is an eigenvalue; if l is not a zero of D ( l ) , then it is not an eigenvalue, so we get
The eigenvalues of the 4° integral equation are all zeros of D ( l ) .
5° has only a finite number of eigenvalues in any finite region of the l -plane.
The [ transpose integral equation ] has the form
(6)
The equation is called the Fr equation
The transposed integral equation of , its corresponding homogeneous equation is
(7)
The kernel of this equation is written as
K 0 ( x , x ) = K ( x , x )
The transposed integral equation has the following properties:
The 1° homogeneous equation (5) and its transposed equation (7) either have only zero solutions at the same time, or both have non-zero solutions.
The 2° homogeneous equation (5) has the same number of linearly independent solutions as its transpose equation (7) .
3° If l is an eigenvalue, the necessary and sufficient condition for the inhomogeneous Fr equation to be solvable is: the free term F ( x ) satisfies the condition
where is any characteristic function of the transposed equation, that is, any solution of the homogeneous equation (7) . If this condition is satisfied, the Fr equation has infinitely many solutions, and all such solutions take the form
where y 0 ( x ) is any particular solution of Fr equation, which is r non-trivial linearly independent solutions of equation (5) , c 1 , c 2 , L , cr are arbitrary constants.
It should be noted that the results of the above equations are exactly similar to the corresponding results regarding the existence and uniqueness of solutions for a system of n linear algebraic equations of n variables .
