§ 3 Volterra's integral equation
[ Volterra integral equations of the second kind ]
The one-dimensional Volterra equations of the second kind are
![]() ( 1 )
( 1 )
This is a special case of the Fr equation ( K ( x, ξ ) =0 when ξ > x ). Assume that F ( x ) is continuous on the interval [ a , b ] , K ( x, ξ ) is continuous on the square k 0 ( a ≤ x ≤ b, a ≤ ξ ≤ b ) , and when ( ξ > x ),
K ( x, ξ )=0
Therefore, when K ( x,x ) ≠ 0 , the kernel has a discontinuity of the first kind x = ξ .
The solution of the integral equation ( 1 ) is expressed in the power series of λ as
![]() ( 2 )
( 2 )
For the function y n ( x ) we have the following recursion formula:
![]() ,
,
![]()
![]()
Set on a finite interval or square, the continuous functions F ( x ) and K ( x, ξ ) satisfy
![]() ,
,
![]()
where m and M are constants. So when sufficiently small, the series ( 2 ) converges absolutely and uniformly on [ a, b ] whose sum y ( x ) is a continuous function and satisfies equation ( 1 ).![]()
can also be used as pre-de-nucleation
![]() ( 3 )
( 3 )
In the formula, the stack kernel K n ( x, ξ ) is calculated by the following recursive formula:
![]() ;
; ![]()
![]()
And it follows that when ξ > x , K n ( x, ξ )=0 . In fact, if ξ > x, then ξ 1 < ξ , thus
K ( ξ , ξ )=0
It can be shown that the series ( 3 ) converges absolutely and uniformly for all values of λ . Thus, the presolution kernel of Volterra's equation ( 1 ) is an integral function and has a unique solution for any λ of the form:
![]()
So the Volterra equation has no eigenvalues, that is, a homogeneous equation
![]()
There is only trivial solution y ( x ) ≡ 0 for any λ . Therefore, if the Fr denominator of equation ( 1 ) is used , it can be found that it has no zeros at all.![]()
[ Special Volterra equation ] Let u ( x ), v ( x ) be two continuous functions defined on x ≥ 0 by the integral
![]()
The defined function is called the convolution (or convolution ) of u ( x ) and v ( x ) of the function.
According to the nature of convolution (that is , the Laplace transform of the convolution of u and v is equal to the product of the Laplace transform of u and v ), the solution of the special Volterra equation (the kernel of which is only related to the difference):
![]()
The problem becomes the inverse transform problem of determining a Laplace transform. To this end, take the Laplace transform on both sides of the above formula, and use the properties of convolution, we have
![]()
have to
![]()
y ( x ) can be determined using a Charaplacian table of transformations or other methods .
[ Volterra integral equations of the first kind ] Volterra integral equations of the first kind
![]() ( 1 )
( 1 )
can be transformed into Volterra integral equations of the second kind. Under the assumption that the kernel is continuously differentiable, there are two transformation methods. One way is to take the derivative on both sides of ( 1 ) to get![]()
![]()
If K ( x,x ) ≠ 0, this equation can be reduced to
![]()
in the formula
![]() ,
,
![]()
Another way is to set
![]()
Then equation ( 1 ) turns into
![]()
Division points
![]()
If K ( x,x ) ≠ 0, this equation can be rewritten as
![]()
in the formula
![]() ,
, ![]()
[ Abel's integral equation ] has the form
![]() (1)
(1)
The Volterra integral equation is called the Abelian integral equation. The integral equation ( 1 ) can be solved by an indirect method under appropriate constraints on the given function F ( x ) . ( 1 ) is divided by ( s is a parameter), and then integrated on both sides, we get![]()
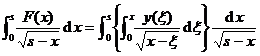
Swap the order of integration on the right side of the above formula and change the limit of integration, it becomes
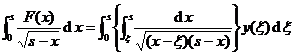 (2)
(2)
Let x = ( s - ξ ) t + ξ , then we have
![]()
Substitute into ( 2 ) formula to have
![]()
or written as
![]()
Taking the derivative of this equation, we get the desired solution as
![]()
Equation ( 1 ) has no continuous solution if F ( x ) cannot make the right-hand side of this equation exist and be continuous .