§ 5 Nonlinear integral equations
[ Integral and Linear Operators ] Consider the expression
![]()
For a given kernel K ( x , ξ ), each function f ( x ) has another function F ( x ) corresponding to it. This correspondence is called an integral operator, denoted as K , namely
F=Kf
The set of those functions f such that the function F = Kf exists is called the domain of operator K.
If operator K satisfies the condition
![]() ( a is a constant)
( a is a constant)
Then K is called a linear operator.
[ Bounded operator and its norm ] If there is a constant M , for all functions f
![]()
Then K is called a bounded operator, where it represents the norm ( modulus ) of the function f . The largest lower bound of all M that makes the above inequality true is called the norm of operator K , denoted as , it can also be defined as![]()
![]()
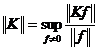
Bounded operators have the following properties:
1° If K 1 and K 2 are bounded operators, then K 1 K 2 is also a bounded operator.
2° If the function K ( x , ξ ) is continuous for all x , ξ , on the finite square k 0 ( a ≤ x ≤ b , a ≤ ξ ≤ b ) , then by
![]()
The defined operator K is a bounded operator.
3° If on the infinite interval [ a, b ] , the function K ( x, ξ ) satisfies
![]()
then by
![]()
The defined operator K is a bounded operator.
[ Theorem of existence of solutions to nonlinear integral equations ] Consider an integral equation of the form
![]()
![]() (1)
(1)
The methods of solving linear integral equations in the previous sections are not applicable to nonlinear integral equations. The existence theorems of just a few solutions are listed below.
Theorem 1 assumes that K ( x , ξ ) is continuous for all x, ξ on the unit square k 0 (0 ≤ x ≤ 1,0 ≤ ξ ≤ 1) , let ô K ( x, ξ ) ô ≤ C ( C ( C is a constant ) , for all ξ on the unit square k 0 , t is also continuous, and ![]()
![]() ( A is a constant )
( A is a constant )
It is also assumed that the Lipschitz condition is satisfied![]()
![]()
where B is a constant independent of ξ . At that time , the integral equation (1) has a unique solution in L 2 [0,1] * .![]()
Theorem 2 assumes that K ( x, ξ ) is continuous with respect to all x, ξ on the unit square k 0 , let
![]() ( C is a constant)
( C is a constant)
![]() satisfy
satisfy
![]() ( B is a constant)
( B is a constant)
and for any ε > 0 , there is δ = δ ( ε ) such that
![]() ( at the time )
( at the time )![]()
in the formula . Then at that time , integral equation (1) has at least one solution in L 2 [0,1] * .![]()
![]()
Theorem 3 assumes that K ( x , ξ ) and are both continuous functions of their independent variables, let S be L 2 [0,1] satisfying ![]()
![]() ( M is a constant)
( M is a constant)
the whole of the function . assumed![]()
![]() ( C is a constant)
( C is a constant)
![]() (everything )
(everything )![]()
And for any ε > 0 , there exists δ = δ ( ε ), such that
![]() ( at the time )
( at the time )![]()
At that time , the integral equation (1) has at least one solution in S.![]()
The condition of this theorem requires that K ( x , ξ ) be continuous, and in fact it can be shown that the same result is obtained as long as the kernel K ( x , ξ ) is square-integrable.
Theorem 4 assumes that the conditions stated in Theorem 3 are satisfied, and let K ( x, ξ ) satisfy ![]()
![]()
At that time , the integral equation (1) has at least one solution in S.![]()