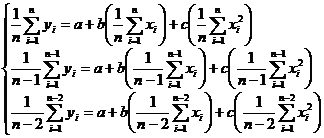§ 3 Arc method and average method of curve fitting
1. The arc method of curve fitting
Circular fitting is a geometric method that depicts a fitted curve through observation points ( model points ) . ![]() It replaces curves with segmented arcs and makes two adjacent arcs have a common tangent. This approach boils down to the following three situations :
It replaces curves with segmented arcs and makes two adjacent arcs have a common tangent. This approach boils down to the following three situations :
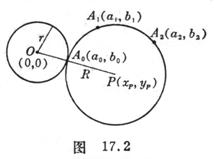
![]() Given circle O and two points outside the circle , , find the circle P , make it pass through the points , and be tangent ( circumscribed or inscribed ) with circle O ( Fig. 17.2 ) .
Given circle O and two points outside the circle , , find the circle P , make it pass through the points , and be tangent ( circumscribed or inscribed ) with circle O ( Fig. 17.2 ) .![]()
![]()
![]()
|
|
Let the radius of the circle O be r and the coordinates of the point O to be ( 0,0 ) . remember
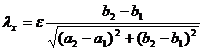

![]() , the symbol is inscribed or excised. remember again
, the symbol is inscribed or excised. remember again
![]()
in the formula
![]()
![]()
![]()
then
( i ) The coordinates of the center of the circle P are![]()
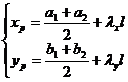
( ii ) The radius R of the circle P is
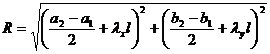
( iii ) The coordinates of the tangent point are![]()
![]()
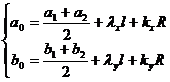
in


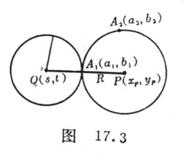
![]() Knowing the circle Q and a point outside the circle , find the circle P so that it passes through the fixed point and is tangent to the circle Q at the fixed point ( Figure 17.3 ) .
Knowing the circle Q and a point outside the circle , find the circle P so that it passes through the fixed point and is tangent to the circle Q at the fixed point ( Figure 17.3 ) .![]()
![]()
![]()
Let the coordinates of the center of the circle Q be ( s, t ) , then
|
|
( i ) The coordinates of the center of the circle P are![]()
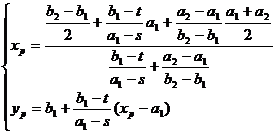
( ii ) The radius R of the circle P is
![]()
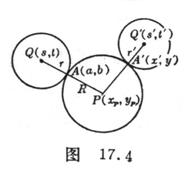
![]() Knowing the circle Q and the circle , find the circle P so that it is tangent to the circle and to the circle Q at a fixed point ( Fig. 17.4 ) .
Knowing the circle Q and the circle , find the circle P so that it is tangent to the circle and to the circle Q at a fixed point ( Fig. 17.4 ) .![]()
![]()
![]()
Let the coordinates of the center of the circle Q be ( s, t ) and the radius be r ; the coordinates of the center of the circle are and the radius is . remember again![]()
![]()
![]()
|
|
![]()
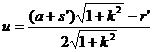
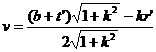
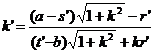
then
( i ) The coordinates of the center of the circle P are![]()
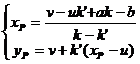
( ii ) The radius R of the circle is
![]()
( iii ) The coordinates ( x', y' ) of the tangent point A' are
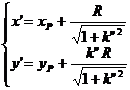
in the formula
![]()
Second, the average method of curve fitting
[ Linear ] If a series of data for two variables ( x, y ) are known to be
|
x |
|
|
y |
|
Suppose x, y satisfy a linear relationship
![]()
Then a and b are determined by the following equations :
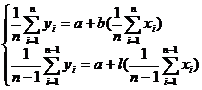
The dispersion of the ordinate between the straight line obtained by this method and each point
![]()
The algebraic sum is zero.
[ Parabolic ] If the straight line does not fit the trend of the known data, then the optional polynomial
![]()
to fit. For example, take the empirical curve as a quadratic polynomial
![]()
a,b,c can be determined by the following three-dimensional linear equations :