§5 Filtering

§ 5 Filtering

Extracting the required information from the data ( or signal ) containing errors ( meaning interference, noise ) , this data processing method is called filtering. Only a few types of least squares ( or least variance ) filtering are described below.

1. Least Squares Filtering

[ Least Squares Filtering for Growing Memory ]

Least Squares Criterion for Filtering

Given a discrete observation system

in the formula

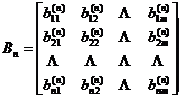
where represents the transpose, which is the observation value at the moment , and is the n -dimensional column vector formed by , called the observation vector; yes , the matrix, where m is a constant; is the n -dimensional column vector, and its component is the error when; is the state vector ( m dimension ) . Suppose the state satisfies the equation

Among them is the m -order square matrix, its elements are all constants, and it is set to be reversible, remember .

If then

is called the optimal estimate in the least squares sense.

Assuming that it is reversible, remember , then it can be deduced

The recursive formula for filtering

The above-mentioned formula for the optimal estimate is not practical on an electronic computer, and a recursive formula is usually used on the computer. can be launched

is an m -dimensional row vector

satisfied .

From the above formula, all historical observations are actually used for the purpose , and as n increases, the number used increases, so this filtering recursion formula is called growth memory.

[ Weighted Least Squares Filtering ] When n is sufficiently large, the earlier historical data is often used in an unfavorable role in estimation. Through weighting, the effect of "too old" data can gradually disappear. The following is an example of an "exponential decline" right.

Select , introduce a diagonal matrix sequence

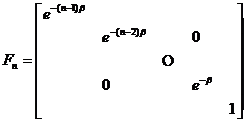
As before, the observation system and the state equation are set as

if time

It is called the optimal valuation in the sense of least squares with the weight of "exponential decline".

can prove

And there is a recursive formula for calculation

is an m -dimensional row vector with the same definition as before.

2. Wiener filter

Wiener filtering and Kalman filtering are both least square deviation filtering, but they are based on known conditions, calculation methods and scope of application are different.

[ Wiener Filtering Criterion ] Suppose you want to get the sequence z ( t ) ( t only takes some integer values ) , and actually get the sequence x ( t ) . So design a linear constant system with impulse response h ( t ) , so that its input quantity is x ( t ) , and the output quantity is

The deviation from z ( t ) is as small as possible under some criterion.

The so-called Wiener filtering problem is to take h ( t ) appropriately so that

When x ( t ) is a deterministic sequence,

When x ( t ) is a random sequence,

[ Single Least Squares Filtering ] Suppose that the filter factor h ( t ) is a sequence consisting of s + 1 equally spaced coefficients, such as

s + 1 is called the length of the filter factor, then the least square filter factor h ( t ) satisfies

or expressed by convolution as

is called the autocorrelation function of the input x ( t ) ( Chapter 16 § 3 ) ,

is called the cross-correlation function of z ( t ) and x ( t ) .

How well the filtered output matches the desired output can be measured by the normalized mean squared error :

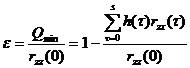
to measure, where

Obviously . At that time , the filtering effect was the best; at that time , the filtering effect was the worst.

Similar results can be obtained when the length of the filter factor is infinite. Use , , to represent the frequency spectrum ^{* of}h ( t ) , respectively , then according to the convolution of the two functions is equivalent to the product of their spectra, the frequency characteristics can be obtained

It shows that the frequency spectrum of the filter factor can be determined by the frequency spectrum of the cross-correlation function and the auto-correlation function.

[ Multi-channel Least Square Filtering ] Multi-channel least square filtering method utilizes the repetition of multi-channel signals to provide more beneficial information.

Set as n - way input, m -way desired output, written as a matrix, respectively

is the multi-channel filter factor, written as a matrix as

-------------------------------

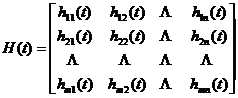
The frequency spectrum of a discrete time series is defined as

When the discrete time series has only finite items, it can be filled with many 0s to become an infinite series and the above definition can be used.

is the m -channel filtered output, written as a matrix as

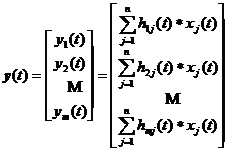
If the length of each input is k +1 , and the length of all filter factors is s +1 , then the length of the filtered output of each channel is k + s +1 .

The so-called multi-channel least square filtering is to appropriately select the multi-channel filter factor ( matrix ) H ( t ) to make the total mean square error

When it is a definite sequence,

When it is a random sequence,

The multi-channel least squares filter factor satisfies the following equation

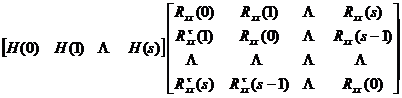
( 1 )

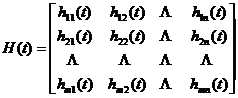
is the multi-channel least squares filter factor, is the matrix,

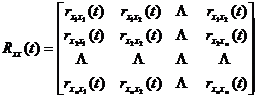
is the transpose matrix of the input autocorrelation function square matrix, called the multi-way autocorrelation matrix ,

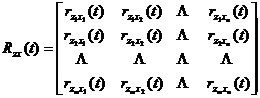
A matrix of cross-correlation functions for the desired output and input .

Equation ( 1 ) is mn ( s + 1) linear simultaneous equations with the filter factor as the unknown . Its solution is the required multi-channel least squares filter factor.

The degree of agreement between the filtered output and the desired output, using the normalized mean square error

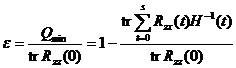
to measure, obviously, . At that time , the multi-channel least square filtering output matched the desired output best; at that time , the matching degree was the worst.

When the length of the filter factor is infinite, the least squares filter factor satisfies the following equation

Expressed in frequency spectrum, we have

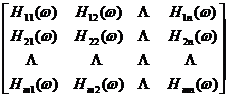
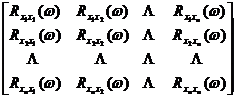
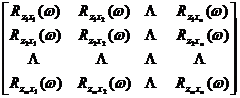
The solution of the above equation is the desired multi-path least squares filter factor.

3. Kalman filter

[ Kalman Filtering for Linear Discrete Systems ]

The dynamic model assumes that an n -dimensional linear dynamic system and a p -dimensional linear observation system are respectively described by the following difference equations :

Or introduce the corresponding symbol simply written as

( 1 )

( 2 )

where ( k is an integer ) satisfies

x ( t )is the n -dimensional state vector,( t )is the m -dimensional dynamic noise vector, z ( t )is the p -dimensional()observation vector, and v ( t )is the p -dimensional()observation noise vector;a matrix, called dynamicnoise matrix, H ( t )is amatrix, called the observation matrix,is a non- singular matrix, called the transition matrix of the system, with the following properties:

(i ) ( for all t , where I is the identity matrix )

( ii ) ( for any )

( iii )

Linear minimum variance estimation If the estimation of the state of the system at time is determined from the dynamic model , the following conditions are satisfied :

( i ) the estimate is a linear function of the observed value ;

( ii ) = minimum value, where is the estimation error ; then this estimation is called the linear minimum variance estimation.

Suppose that through the p -dimensional linear observation system ( 2 ) , from the 1st time to the kth time, the state of the n -dimensional linear dynamic system ( 1 ) has been observed k times , and according to the k observation data, the state of the jth time An estimate is made , and the estimated error is , and the mean squared error of the estimate is denoted as . At the time , it was called forecasting or extrapolation, at the time , it was called interpolation. Especially when j = k is called filtering, and is abbreviated .

The Kalman filter formula is set in the above dynamic model, and the dynamic noise and observation noise are uncorrelated zero-mean white noise sequences; that is, for all k, j

mean , mean square error

Let the statistical characteristics of the initial state be

and are not related to

Then the optimal linear filter can be calculated recursively by the following formula

its initial value ;

Called the weighting matrix or gain matrix, it is the covariance matrix of the optimal estimation error , the I in parentheses represents the identity matrix, and the last equation is called the covariance update equation.

At this time, the optimal linear prediction ( extrapolation ) is estimated as

( j > k )

[ Kalman Filtering for Continuous Time Systems ]

The dynamic model assumes that the state equation is

( 1 )

The observation equation is

where is a random process of n -dimensional vector type, and is a random process of p -dimensional vector type. , respectively, are m -dimensional ( ) and p -dimensional vector-type, uncorrelated white noise processes with zero mean, namely

In the formula, Q ( t ) and R ( t ) are both continuously differentiable, symmetric and non-negative definite matrices for time t ; they are Dirac functions. And F ( t ) , G ( t ) and H ( t ) are respectively matrices whose elements are non-random functions or constants of t .

The linear minimum variance estimation assumes the known ( observed ) value ( ) , and is calculated by the formula

represents a linear estimate such that

= minimum value

Such an estimate is called a linear minimum variance estimate, where the filter factor matrix, each element of which is continuously differentiable for both independent variables.